Java数据结构----排序
目录
稳定性定义
插入排序
直接插入排序
希尔排序（缩小增量排序）
选择排序
直接选择排序：
堆排序
交换排序
冒泡排序
快速排序
1.左右指针法（hoare版本）
2.挖坑法
3.前后指针法
归并排序
稳定性定义
假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持 不变，即在原序列中，r[i]=r[j] ，且 r[i] 在 r[j] 之前，而在排序后的序列中， r[i] 仍在 r[j] 之前，则称这种排序算法是稳 定的；否则称为不稳定的。
插入排序
直接插入排序
直接插入排序是一种简单的插入排序法，其基本思想是： 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到 一个新的有序序列 。
当插入第 i(i>=1) 个元素时，前面的 array[0],array[1],…,array[i-1] 已经排好序，此时用 array[i] 的排序码与 array[i-1],array[i-2],…的排序码顺序进行比较，找到插入位置即将 array[i] 插入，原来位置上的元素顺序后移。
public static void sort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
for (int j =i; j >=1; j--) {
if(arr[j]直接插入排序的特性总结：1. 元素集合越接近有序，直接插入排序算法的时间效率越高2. 时间复杂度： O(N^2)3. 空间复杂度： O(1) ，它是一种稳定的排序算法4. 稳定性：稳定
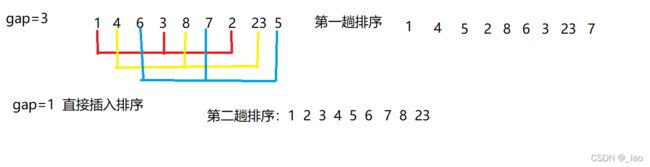
希尔排序（缩小增量排序）
希尔排序法又称缩小增量法。希尔排序法的基本思想是： 先选定一个整数，把待排序文件中所有记录分成几组，所 有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，重复上述分组和排序的工作。当到达 =1 时，所有记录在统一组内排好序 。
public static void sort2(int[] arr,int d){
for (int i = d; i < arr.length; i++) {
for (int j = i-d; j>=0; j-=d) {
if(arr[j]>arr[j+d]){
int tmp=arr[j];
arr[j]=arr[j+d];
arr[j+d]=tmp;
}
}
}
}
public static void shell(int[] arr){
int gap=arr.length/2;
while(gap>1){
sort2(arr,gap);
gap/=2;
}
sort2(arr,1);
}希尔排序的特性总结：1. 希尔排序是对直接插入排序的优化。2. 当 gap > 1 时都是预排序，目的是让数组更接近于有序。当 gap == 1 时，数组已经接近有序的了，这样就会很 快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。3. 希尔排序的时间复杂度不好计算，因为 gap 的取值方法很多，导致很难去计算，因此在好些树中给出的希尔排 序的时间复杂度都不固定，约o(N^1.3~N^1.5)4.空间复杂度O(1)5. 稳定性：不稳定
选择排序
基本思想：每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元 素排完 。
直接选择排序：
- 在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
- 若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换
- 在剩余的array[i]--array[n-2]（array[i+1]--array[n-1]）集合中，重复上述步骤，直到集合剩余1个元素
public static void sort3(int[] arr){
for (int i = 0; i < arr.length; i++) {
for (int j=i+1;j< arr.length;j++){
if(arr[i]>arr[j]){
int tmp=arr[i];
arr[i]=arr[j];
arr[j]=tmp;
}
}
}
}直接选择排序的特性总结：1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用2. 时间复杂度： O(N^2)3. 空间复杂度： O(1)4. 稳定性：不稳定
堆排序
堆排序 (Heapsort) 是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。
public static void sort4(int[] arr){
if(arr==null||arr.length==0){
return;
}
int len= arr.length;
//将待排序的序列，变成一个大根堆的数组
buildMaxHeap(arr,len);
//交换堆顶和当前末尾的节点，重置大根堆
for (int i = len-1; i >0 ; i--) {
swap(arr,0,i);
len--;
heapify(arr,0,len);
}
}
public static void buildMaxHeap(int[] arr,int len){
//从最后一个非叶子节点开始向前遍历
for (int i=(len/2)-1;i>=0;i--) {
heapify(arr,i,len);
}
}
public static void heapify(int[] arr,int i,int len){
//先根据堆的性质，找出它左右节点的索引
int left=2*i+1;
int right=2*i+2;
int index=i;//默认当前节点是最大值
if(leftarr[index]){
index=left;
}
if (rightarr[index]){
index=right;
}
if(index!=i){
//如果最大值不是当前非子叶节点的值，那么就把当前节点和最大值的节点互换
swap(arr,i,index);
//互换之后，子节点的值变了，如果该子节点也有自己的子节点，仍需要继续调整
heapify(arr,index,len);
}
}
private static void swap(int[] arr,int i,int j){
int tmp=arr[i];
arr[i]=arr[j];
arr[j]=tmp;
}
堆排序的特性总结
1. 堆排序使用堆来选数，效率就高了很多。2. 时间复杂度： O(N*logN)3. 空间复杂度： O(1)4. 稳定性：不稳定
交换排序
基本思想：所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置，交换排序的特点是：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。
冒泡排序
public static void sort5(int[] arr){
for (int i = 0; i < arr.length-1; i++) {
for (int j = 0; j < arr.length-1-i; j++) {
if(arr[j]>arr[j+1]){
int tmp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=tmp;
}
}
}
}【 冒泡排序的特性总结 】1. 冒泡排序是一种非常容易理解的排序2. 时间复杂度： O(N^2)3. 空间复杂度： O(1)4. 稳定性：稳定
快速排序
基本思想：任取待排序元素序列中的某元 素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有 元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
1.左右指针法（hoare版本）
思路：
1.选出一个key，一般是最左边或是最右边的。
2.定义一个begin和end，begin从左向右走，end从右向左走。（注意：若选择最左边的数据作为key，需要end先走；若选择最右边的数据作为key，需要begin先走）
3.走的过程中，若end遇到小于key的数，则停下，begin开始走，直到begin遇到一个大于key的数时，交换begin和end的内容进行交换，end再开始走，如此重复直到begin和end相遇，然后将相遇点和key进行交换。（此时key的左边都是小于key的数，key的右边都是大于key的数）
4.将key的左右序列再次进行这种排序，直到左右序列只有一个数据或是不存在时，此时此部分已有序。
代码：
public static void sort6(int[] arr,int begin,int end){
if(begin>end){
return;
}
int i=begin;
int j=end;
int key=arr[i];//基准位
while(i=arr[i]&&i 2.挖坑法
思路：
1.选出一个数据（一般是最左边或是最右边）存放在key变量中，在该数据形成一个坑。
2.还是定义一个L和一个R，L从左向右走，R从右向左走（若在左边挖坑，则右边先走，若在右边挖坑，则左边先走）
后面就和左右指针法的思路一样
代码：
public static void sort7(int[] arr,int begin,int end){
if(begin>end){
return;
}
int i=begin;
int j=end;
int tmp=arr[i];//基准位
while(i=arr[i]&&i 3.前后指针法
思路：
1.选出一个key，一般是最左边或是最右边的。
2.起始时，prev指针指向序列开头，cur指针指向prev+1。
3.若cur指向的内容小于key，则prev先向后移动一位，然后交换prev和cur指针指向的内容，然后cur++；若cur指向的内容大于key，则cur直接++，直到cur到达end的位置，此时将key和++prev交换即可
代码：
public static int sort8(int[] arr,int left,int right){
int prev=left;
int cur;
for ( cur = left; cur 快速排序的特性总结
1.时间复杂度： O(N*logN)2. 空间复杂度： O(logN)3. 稳定性：不稳定
归并排序
基本思想：
归并排序（ MERGE-SORT ）是建立在归并操作上的一种有效的排序算法 , 该算法是采用分治法（ Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使 子序列段间有序。
public static void mergeSort(int[] data) {
sort(data, 0, data.length - 1);
}
public static void sort(int[] data, int left, int right) {
if (left >= right)
return;
// 找出中间索引
int center = (left + right) / 2;
// 对左边数组进行递归
sort(data, left, center);
// 对右边数组进行递归
sort(data, center + 1, right);
// 合并
merge(data, left, center, right);
print(data);
}
/**
* 将两个数组进行归并，归并前面2个数组已有序，归并后依然有序
*
* @param data
* 数组对象
* @param left
* 左数组的第一个元素的索引
* @param center
* 左数组的最后一个元素的索引，center+1是右数组第一个元素的索引
* @param right
* 右数组最后一个元素的索引
*/
public static void merge(int[] data, int left, int center, int right) {
// 临时数组
int[] tmpArr = new int[data.length];
// 右数组第一个元素索引
int mid = center + 1;
// third 记录临时数组的索引
int third = left;
// 缓存左数组第一个元素的索引
int tmp = left;
while (left <= center && mid <= right) {
// 从两个数组中取出最小的放入临时数组
if (data[left] <= data[mid]) {
tmpArr[third++] = data[left++];
} else {
tmpArr[third++] = data[mid++];
}
}
// 剩余部分依次放入临时数组（实际上两个while只会执行其中一个）
while (mid <= right) {
tmpArr[third++] = data[mid++];
}
while (left <= center) {
tmpArr[third++] = data[left++];
}
// 将临时数组中的内容拷贝回原数组中
// （原left-right范围的内容被复制回原数组）
while (tmp <= right) {
data[tmp] = tmpArr[tmp++];
}
}
public static void print(int[] data) {
for (int i = 0; i < data.length; i++) {
System.out.print(data[i] + "\t");
}
System.out.println();
}归并排序的特性总结
1.归并的缺点在于需要 O(N) 的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。2. 时间复杂度： O(N*logN)3. 空间复杂度： O(N)4. 稳定性：稳定