用 python 解决线性代数中的矩阵运算
- 矩阵叉乘
- 矩阵求逆
- 矩阵转置
- 假定AX=B,求解未知矩阵X
- 矩阵的行列式值|matrix|
- 未完待续。。。。。
import sys
from PyQt5.QtWidgets import *
import numpy as np
class Form(QDialog):
def __init__(self, parent=None):
super().__init__(parent)
grid = QGridLayout()
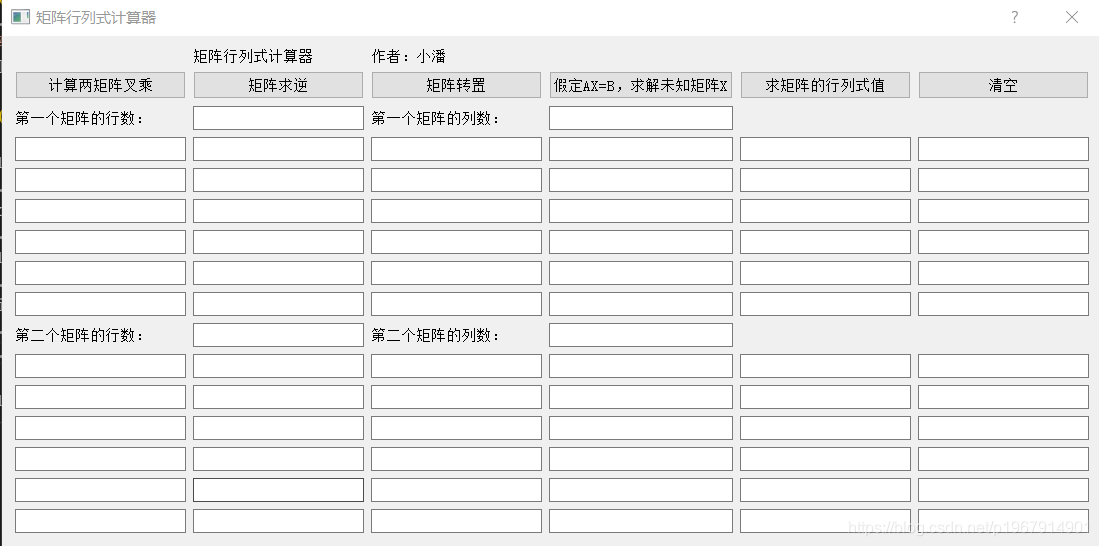
self.setWindowTitle("矩阵行列式计算器")
self.Title = QLabel("矩阵行列式计算器")
grid.addWidget(self.Title, 0, 1)
self.Title = QLabel("作者:小潘")
grid.addWidget(self.Title, 0, 2)
titles = ['计算两矩阵叉乘', '矩阵求逆', '矩阵转置', '假定AX=B,求解未知矩阵X', '求矩阵的行列式值', '清空']
func = [self.multiplication_cross, self.cal_inverse, self.cal_transposition, self.solve_equations, self.cal_value, self.clear]
for index, title in enumerate(titles):
self.set_button(title, 1, index, grid, func[index])
self.textTitle1 = QLabel("第一个矩阵的行数:")
grid.addWidget(self.textTitle1, 3, 0)
self.hang1 = QLineEdit(self)
grid.addWidget(self.hang1, 3, 1)
self.textTitle1 = QLabel("第一个矩阵的列数:")
grid.addWidget(self.textTitle1, 3, 2)
self.lie1 = QLineEdit(self)
grid.addWidget(self.lie1, 3, 3)
self.texts1 = [self.set_text(i, 4, grid) for i in range(36)]
self.textTitle2 = QLabel("第二个矩阵的行数:")
grid.addWidget(self.textTitle2, 10, 0)
self.hang2 = QLineEdit(self)
grid.addWidget(self.hang2, 10, 1)
self.textTitle2 = QLabel("第二个矩阵的列数:")
grid.addWidget(self.textTitle2, 10, 2)
self.lie2 = QLineEdit(self)
grid.addWidget(self.lie2, 10, 3)
self.texts2 = [self.set_text(i, 11, grid) for i in range(36)]
self.setLayout(grid)
def set_button(self, title, x, y, grid, cal):
bt = QPushButton(title)
bt.setParent(self)
grid.addWidget(bt, x, y)
bt.clicked.connect(cal)
def set_text(self, i, y, grid):
text = QLineEdit(self)
grid.addWidget(text, y + i // 6, 0 + i % 6)
return text
def clear(self):
self.hang1.setText('')
self.lie1.setText('')
self.hang2.setText('')
self.lie2.setText('')
for i in range(36):
self.texts1[i].setText('')
self.texts2[i].setText('')
def get_matrix(self):
hang1 = int(self.hang1.text() if self.hang1.text() != '' else 0)
lie1 = int(self.lie1.text() if self.lie1.text() != '' else 0)
hang2 = int(self.hang2.text() if self.hang2.text() != '' else 0)
lie2 = int(self.lie2.text() if self.lie2.text() != '' else 0)
matrix1, matrix2 = [[] for i in range(hang1)], [[] for i in range(hang2)]
for i in range(hang1):
for j in range(lie1):
matrix1[i].append(eval(self.texts1[i*6+j].text()))
for i in range(hang2):
for j in range(lie2):
matrix2[i].append(eval(self.texts2[i*6+j].text()))
return matrix1, matrix2
'''
description: 矩阵叉乘 matrix1 左乘 matrix2
param {matrix1, matrix2} 多维数组
return {matrix} 叉乘后的矩阵
Date Changed:
'''
def multiplication_cross(self):
matrix1, matrix2 = self.get_matrix()
pass
a, b = np.mat(matrix1), np.mat(matrix2)
print('叉乘后的矩阵的矩阵为:')
print(a * b)
'''
description: 矩阵求逆
param {matrix} 多维数组
return {matrix} 逆矩阵
Date Changed:
'''
def cal_inverse(self, matrix):
matrix1, matrix2 = self.get_matrix()
print('逆矩阵为:')
print(np.mat(matrix1).I)
'''
description: 矩阵转置
param {matrix} 多维数组
return {matrix} 转置矩阵
Date Changed:
'''
def cal_transposition(self, matrix):
matrix1, matrix2 = self.get_matrix()
print('转置矩阵为:')
print(np.mat(matrix1).T)
'''
description: 假定AX=B,求解未知矩阵X
param {A, B} 多维数组
return {X} 矩阵X
Date Changed:
'''
def solve_equations (self):
A, B = self.get_matrix()
print('解得X矩阵为:')
print(np.linalg.solve(A, B))
'''
description: 矩阵的行列式值|matrix|
param {matrix} 多维数组
return {number} 矩阵的行列式值
Date Changed:
'''
def cal_value(self, matrix):
matrix1, matrix2 = self.get_matrix()
print('矩阵行列式的值为:')
print(np.linalg.det(matrix1))
if __name__ == '__main__':
app = QApplication(sys.argv)
form = Form()
form.show()
app.exec_()
