概率统计Python计算:F分布分位点计算
设 X X X, Y Y Y相互独立,且分别服从 χ 2 ( m ) \chi^2(m) χ2(m)和 χ 2 ( n ) \chi^2(n) χ2(n),则 X Y \frac{X}{Y} YX~ F ( m − 1 , n − 1 ) F(m-1, n-1) F(m−1,n−1),即 X Y \frac{X}{Y} YX服从自由度为 m m m和 n n n的 F F F分布。服从 F ( m − 1 , n − 1 ) F(m-1, n-1) F(m−1,n−1)分布的随机变量 X X X的概率密度函数为
ψ ( x ) = { Γ ( m + n 2 ) ( m n ) m 2 x m 2 − 1 Γ ( m 2 ) Γ ( n 2 ) ( 1 + m n x ) m + n 2 x ≥ 0 0 x < 0 {\psi(x)=}\begin{cases} {}\frac{\Gamma\left(\frac{m+n}{2}\right)\left(\frac{m}{n}\right)^{\frac{m}{2}}x^{\frac{m}{2}-1}}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)(1+\frac{m}{n}x)^{\frac{m+n}{2}}}&x\geq0\\ 0&x<0 \end{cases} ψ(x)=⎩⎨⎧Γ(2m)Γ(2n)(1+nmx)2m+nΓ(2m+n)(nm)2mx2m−10x≥0x<0
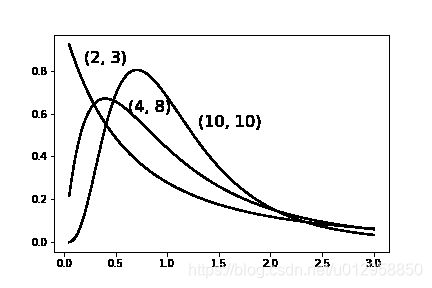
下图展示了 F F F分布的自由度 ( m , n ) (m,n) (m,n)的几个不同组合的密度函数图像。
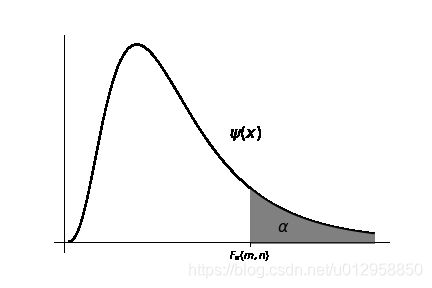
对应给定的显著水平 α \alpha α,单侧右分位点 F α ( m , n ) F_{\alpha}(m,n) Fα(m,n)满足 P ( X ≥ F α ( m , n ) ) = α P(X\geq F_{\alpha}(m,n))=\alpha P(X≥Fα(m,n))=α,如下图所示。
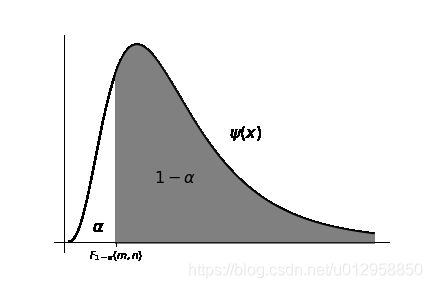
单侧左分位点记为 F 1 − α ( m , n ) F_{1-\alpha}(m,n) F1−α(m,n),满足 P ( X ≥ F 1 − α ( m , n ) ) = 1 − α P(X\geq F_{1-\alpha}(m,n))=1-\alpha P(X≥F1−α(m,n))=1−α,如下图所示。
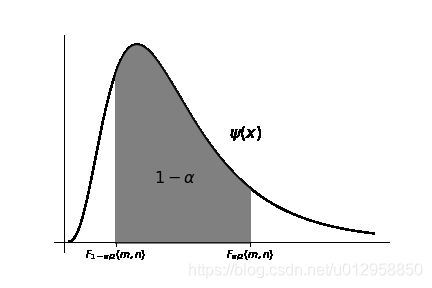
而双侧左右分位点 F 1 − α / 2 ( m , n ) F_{1-\alpha/2}(m,n) F1−α/2(m,n)和 F α / 2 ( m , n ) F_{\alpha/2}(m,n) Fα/2(m,n)满足 P ( F 1 − α / 2 ( m , n ) ( < X < F α / 2 ( m , n ) ) ≥ 1 − α P(F_{1-\alpha/2}(m,n)(
Python的scipy.stats包中,连续型分布类 rv_continuous的f对象表示 F F F分布,常用函数的调用接口见下表。
| 函数名 | 参数 | 意义 |
|---|---|---|
| ppf | q:表示显著水平 α \alpha α,dfn,dfd:表示分布的自由度 m m m和 n n n | 单侧左分位点 F 1 − α ( m , n ) F_{1-\alpha}(m,n) F1−α(m,n) |
| isf | q,dfn, dfd:与上同 | 单侧右分位点 F α ( m , n ) F_{\alpha}(m,n) Fα(m,n) |
| interval | alpha:表示置信水平 1 − α 1-\alpha 1−α,dfn, dfd:与上同 | 双侧分位点 F 1 − α / 2 ( m , n ) F_{1-\alpha/2}(m,n) F1−α/2(m,n)和 F α / 2 ( m , n ) F_{\alpha/2}(m, n) Fα/2(m,n) |
例1 设检验水平 α = 0.05 \alpha=0.05 α=0.05,计算自由度 m = 12 m=12 m=12, n = 9 n=9 n=9的 F F F分布的单侧分位点和双侧分位点。
解:下列代码完成本例计算。
from scipy.stats import f #导入f
m=12 #设置自由度m
n=9 #设置自由度n
alpha=0.05 #设置alpha
a=f.ppf(q=alpha, dfn=m, dfd=n) #单侧左分位点
b=f.isf(q=alpha, dfn=m, dfd=n) #单侧右分位点
print('单侧左、右分位点:a=%.4f, b=%.4f'%(a, b))
a, b=f.interval(1-alpha, dfn=m, dfd=n) #双侧分位点
print('双侧左、右分位点:a=%.4f, b=%.4f'%(a, b))
运行程序,输出
单侧左、右分位点:a=0.3576, b=3.0729
双侧左、右分位点:a=0.2910, b=3.8682
写博不易,敬请支持:
如果阅读本文于您有所获,敬请点赞、评论、收藏,谢谢大家的支持!
返回《导引》