Python机器学习实战：掌握这四个特征选择方法，提升模型预测性能

机器学习实战：这里没有艰深晦涩的数学理论，我们将用简单的案例和大量的示例代码，向大家介绍机器学习的核心概念。我们的目标是教会大家用Python构建机器学习模型，解决现实世界的难题。

当数据集包含很多特征，例如超过100个，该如何处理？

有的特征可能是噪音，没有预测能力，部分特征之间可能高度相关，如果把所有数据喂到机器学习算法，会导致糟糕的结果：

1. 预测精度低，这点容易理解，即所谓垃圾进垃圾出(garbage in, garbage out)
2. 低泛化能力
3. 模型训练的时间更长

为了解决这个问题，需要使用特征选择(feature selection).

所谓特征选择，即根据某个标准，从众多特征中挑选出预测能力最强的特征。

有四种常用的方法，sklearn提供了相应的实现接口：

1. 单变量选择
2. 递归消除
3. 特征重要性
4. PCA

参考教程：

• 如何用sklearn实现特征选择
• 特征选择和数据可视化

准备数据

我们用Pima-Indians-Diabetes数据集做说明，数据集包含768个观测值和8个特征，目标是预测病人是否患糖尿病。

特征描述：

• Pregnancies: 怀孕次数
• Glucose: 口服葡萄糖耐量测试中2小时的血浆葡萄糖浓度
• BloodPressure: 舒张压（毫米汞柱）
• SkinThickness: 三头肌皮肤褶皱厚度（毫米）
• Insulin: 2小时血清胰岛素（mu U / ml）
• BMI: 体重指数（体重（kg）/（身高（m））^ 2）
• DiatetesPedigreeFunction: 糖尿病谱系功能
• Age: 年龄（岁）

目标变量：1：糖尿病检测呈阳性；0：检测结果为阴性

import warnings
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

plt.style.use("ggplot")

warnings.filterwarnings("ignore")

diabetes = pd.read_csv("./datasets/diabetes.csv")
diabetes.head()

	Pregnancies	Glucose	BloodPressure	SkinThickness	Insulin	BMI	DiabetesPedigreeFunction	Age	Outcome
0	6	148	72	35	0	33.6	0.627	50	1
1	1	85	66	29	0	26.6	0.351	31	0
2	8	183	64	0	0	23.3	0.672	32	1
3	1	89	66	23	94	28.1	0.167	21	0
4	0	137	40	35	168	43.1	2.288	33	1

X = diabetes.iloc[:, 0:8]
y = diabetes.iloc[:, 8]

1. 单变量选择

什么单变量选择？

选择与目标变量相关性最高的特征，剔除无关变量。

单变量选择是最简单的特征选择方法之一，但有一个明显的缺点，它仅仅考虑了特征与目标变量的相关性，没有考虑特征与特征之间的相关性，所以无法剔除重复的特征。

如何测量相关性？

用统计检验(如F检验，卡方检验等)测试特征和目标变量的关联程度。

sklearn.feature_selection提供了3个接口：

• SelectKBest: 筛选k个相关性最高的特征，最常用。
• SelectPercentile: 筛选得分排名前k分位数的特征。
• GenericUnivariateSelect: 根据用户自定义评分函数进行筛选。

有3种常用的统计检验：

• f_classif：方差分析(ANOVA)，适用于分类问题，特征是数值变量，目标是分类变量。
• chi2：差方分析，适用于分类问题，要求特征是计数或二元变量（正值）。
• f_regression：适用于回归问题，特征和目标变量均为数值变量。

所有检验都返回一个分值和p-value，分值和p-value越高表示特征与目标变量的关联程度越高。

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif

# 创建selector，定义检验方法，因为这是分类问题，而且特征全部是数值变量，选择'f_classif'
# 保留关联程度最高的4个特征
selector = SelectKBest(score_func=f_classif, k=4)

# 拟合数据，同时提供特征和目标变量
results = selector.fit(X, y)

# 查看每个特征的分数和p-value
# results.scores_: 每个特征的分数
# results.pvalues_: 每个特征的p-value
# results.get_support(): 返回一个布尔向量，True表示选择该特征，False表示放弃，也可以返回索引
features = pd.DataFrame({
    "feature": X.columns,
    "score": results.scores_,
    "pvalue": results.pvalues_,
    "select": results.get_support()
})
features.sort_values("score", ascending=False)

	feature	score	pvalue	select
1	Glucose	213.161752	8.935432e-43	True
5	BMI	71.772072	1.229807e-16	True
7	Age	46.140611	2.209975e-11	True
0	Pregnancies	39.670227	5.065127e-10	True
6	DiabetesPedigreeFunction	23.871300	1.254607e-06	False
4	Insulin	13.281108	2.861865e-04	False
3	SkinThickness	4.304381	3.834770e-02	False
2	BloodPressure	3.256950	7.151390e-02	False

调用results.transform()直接返回经过筛选的特征。

X_new = results.transform(X)
X_new

array([[  6. , 148. ,  33.6,  50. ],
       [  1. ,  85. ,  26.6,  31. ],
       [  8. , 183. ,  23.3,  32. ],
       ...,
       [  5. , 121. ,  26.2,  30. ],
       [  1. , 126. ,  30.1,  47. ],
       [  1. ,  93. ,  30.4,  23. ]])

调用results.get_support()返回得分最高的K个特征的索引。

X_new_index = results.get_support(indices=True)
X_new = X.iloc[:, X_new_index]
X_new.head()

	Pregnancies	Glucose	BMI	Age
0	6	148	33.6	50
1	1	85	26.6	31
2	8	183	23.3	32
3	1	89	28.1	21
4	0	137	43.1	33

2. 递归消除

递归消除：RFE, Recursive Features Elimination.

递归消除的核心思想是通过反复迭代，剔除没有预测意义的特征，与向后逐步回归非常相似，属于纯技术性的变量选择。

步骤：

1. 使用所有特征先创建一个基准模型
2. 剔除一个特征，创建新模型，记录新模型的预测精度
   • 如果预测精度比基准模型高，剔除该特征
   • 如果预测精度比基准模型低，保留该特征
3. 重复第二步，直到预测精度保持稳定

sklearn.feature_selection提供了两个接口：

• RFE: 可指定选择的特征数。
• RFECV: 根据k折交叉验证评分自动选择最优特征。

单变量选择和递归消除应结合使用，它们的功能是互补的，单变量选择剔除了无关变量，递归消除剔除了相关特征

from sklearn.linear_model import LogisticRegression
from sklearn.feature_selection import RFECV

# 创建筛选器
selector = RFECV(
    estimator=LogisticRegression(),  # 由于这是分类问题，选择简单的逻辑回归
    min_features_to_select=3,  # 选择的最小特征数量
    cv=5,  # 交叉验证折数
    scoring="accuracy",  # 评估预测精度的指标
    n_jobs=-1  # 使用所有CPU运算
)

# 拟合数据
results = selector.fit(X, y)

# 查看结果
# results.n_features_: 最终选择的特征数量
# results.support_: 布尔向量，True表示保留特征，False表示剔除特征
# results.ranking_: 特征等级，1表示最高优先级，即应该保留的特征
print("Number of selected features = %d" % results.n_features_)
print("Selected features: %s" % results.support_)
print("Feature ranking: %s" % results.ranking_)

Number of selected features = 5
Selected features: [ True  True False False False  True  True  True]
Feature ranking: [1 1 2 3 4 1 1 1]

调用results.transform()筛选最重要的特征。

X_new = results.transform(X)
X_new

array([[  6.   , 148.   ,  33.6  ,   0.627,  50.   ],
       [  1.   ,  85.   ,  26.6  ,   0.351,  31.   ],
       [  8.   , 183.   ,  23.3  ,   0.672,  32.   ],
       ...,
       [  5.   , 121.   ,  26.2  ,   0.245,  30.   ],
       [  1.   , 126.   ,  30.1  ,   0.349,  47.   ],
       [  1.   ,  93.   ,  30.4  ,   0.315,  23.   ]])

根据拟合结果自行筛选。

X_new = X.loc[:, results.support_]
X_new.head()

	Pregnancies	Glucose	BMI	DiabetesPedigreeFunction	Age
0	6	148	33.6	0.627	50
1	1	85	26.6	0.351	31
2	8	183	23.3	0.672	32
3	1	89	28.1	0.167	21
4	0	137	43.1	2.288	33

3. 特征重要性

我们可以量化特征的重要程度，重要程度越高，对模型准确预测的贡献越大，反之贡献越低。

要评估特征重要性，需要借助以树模型为基础的集成学习算法，最常用的是随机森林(RandomForest)。

用随机森林拟合训练集后，可以从’feature_importances_'属性中获取特征重要性，用户可根据预先设定的阈值选择最重要的特征。

from sklearn.ensemble import RandomForestClassifier

# 创建分类器
model = RandomForestClassifier(random_state=123)

# 拟合数据
model.fit(X, y)

# 提取特征重要性
importance = pd.Series(model.feature_importances_, index=X.columns)
importance = importance.sort_values()

# 可视化
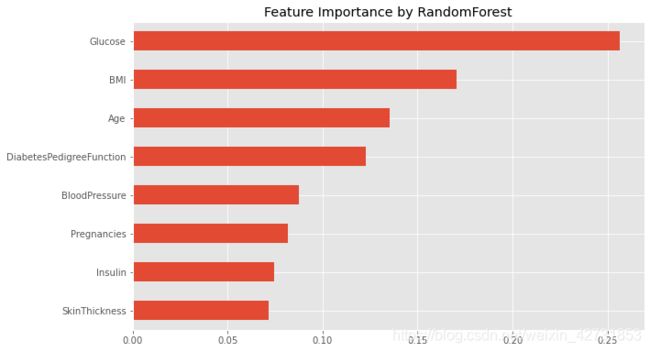
ax = importance.plot.barh(figsize = (10, 6.18), title="Feature Importance by RandomForest")

上图显示，最重要的3个特征分别是’Glucose’,‘BMI’,‘Age’，这都包含在单变量选择和递归消除的结果中。

4. PCA

PCA(Principle Component Analysis): 主成分分析。

PCA是一种降维技术(dimension reduction)，属于无监督机器学习算法，也可用于特征选择。

PCA的核心原理是将大量的相关变量转化为几组无关变量，这些无关变量称为主成分，它们能够保留原始数据的大部分变异。

拟合PCA模型前要先选择约简的维数，这个步骤带有主观判断，如果对问题和数据集缺乏深入理解，很难做出一个正确的选择，当然可以用数学技巧解决这个问题。

接下来用sklearn实现PCA。

from sklearn.decomposition import PCA

# 创建PCA对象，选择3个主成分
pca = PCA(n_components=3)

# 提取主成分
# PCA是无监督机器学习算法，不需要提供目标变量
res = pca.fit_transform(X)

# 获取总的解释方差比率
total_evr = np.sum(pca.explained_variance_ratio_)

# 查看结果
print(f"original features: {X.shape}")
print(f"transform features: {res.shape}")
print(f"explained variance ratio: {total_evr * 100:.2f}%")
print(res)

original features: (768, 8)
transform features: (768, 3)
explained variance ratio: 97.59%
[[-75.71465491 -35.95078264  -7.26078895]
 [-82.3582676   28.90821322  -5.49667139]
 [-74.63064344 -67.90649647  19.46180812]
 ...
 [ 32.11319827   3.3766648   -1.58786446]
 [-80.21449431 -14.18601977  12.3512639 ]
 [-81.30814972  21.62149606  -8.15276833]]

调用pca.fit_transform得到一个(n_samples, n_components)的数组，每一列都代表一个主成分，它们是原始特征的线性组合。

这个数组就是新的"特征矩阵"。

用PCA做特征选择的好处在于，能够创建几个"新特征"来代替数十个原始特征，数据集的维度大大降低，这些新特征不仅能够包含原始数据的大部分变异(方差)，而且彼此间不相关。

缺点是无法从经济意义上解读"新特征"，因为每个主成分都是原始特征的线性组合，从上面的数组就可以看出，它们与原始特征完全不同。

如果喜欢我们的文章，记得点赞和收藏哦，我们每天都会为大家带来Python，数据科学和量化交易的精品内容。

【关于我们】

蜂鸟数据：国内领先的金融数据API提供商。

蜂鸟数据团队由业界顶尖的数据工程师，数据科学家和宽客组成，我们正努力构建一个强大的金融数据库，并提供API接口，目标是令金融数据开源化和平民化。

浏览并测试我们接口吧，目前覆盖股票，外汇，商品期货，数字货币和宏观经济领域，包括实时报价(tick)和历史数据(分钟)，提供REST API和Websocket两种接入方式，能够满足金融分析师，量化交易和理财app的需求。

需要金融数据？利用蜂鸟API将数据整合到您的应用

如果您准备好了，请登录蜂鸟官网，注册免费获取API密钥，然后开始探索我们的金融数据库吧。