机器学习笔记11-FP-growth算法
FP-growth算法
FP-growth算法是一个频繁项集发现算法,它只需要对数据库进行2次扫描,而Apriori算法对于每个潜在的频繁项集都会扫描数据集判定给定模式是否频繁,因此FP-growth算法速度要比Apriori算法快。
FP-growth算法将数据存储在一种称为FP树的紧凑数据结构中。
它通过链接来连接相似元素,被连起来的元素项可以看成一个链表。
1.构建FP树
FP-growth算法的第一次遍历数据集会获得每个元素项的出现频率。接下来,去掉不满足最小支持度的元素项。下一步构建FP树。在构建时,读入每个项集并将其添加到一条已经存在的路径中。如果该路径不存在,创建一条新路径。每个事务就是一个无序集合。假设有集合{z,x,y}和{y,z,r},那么在FP树中 , 相同项会只表示一次。为了解决此问题,在将集合添加到树之前,需要对每个集合进行排序。排序基于元素项的绝对出现频率来进行。
对事务记录过滤和排序之后,就可以构建FP树了,即第二次遍历,向其中不断地添加频繁项集,如果树中已存在现有元素,则增加现有元素的值;如果现有元素不存在,则向树添加一个分支。如下图:
最终构成的FP树如下图所示:
2.从FP树中挖掘频繁项集
有了FP树之后,就可以抽取频繁项集了。这里的思路与Apriori算法大致类似,首先从单元素集合开始,然后在此基础上逐步构建更大的集合。从FP树中抽取频繁项集的三个基本步骤如下:
(1)从FP树中获得条件模式基;
(2)利用条件模式基,构建一个条件FP树;
(3)迭代重复步骤(1)和步骤(2),直到树包含一个元素项为止。
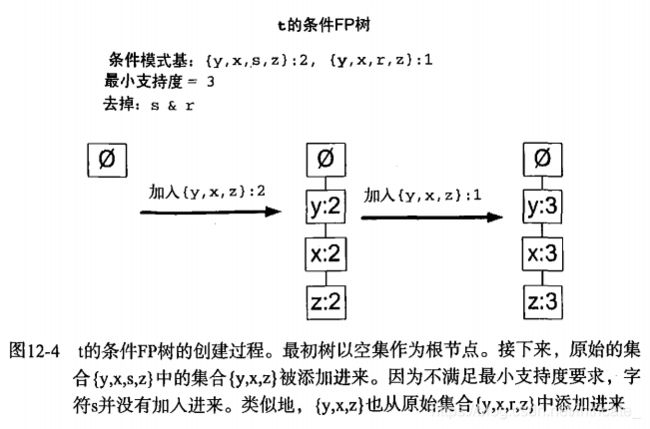
对于每一个频繁项,都要创建一颗条件FP树。例如,假定为频繁项{t}创建一个条件FP树,然后得到频繁项集{t,y}、{t,x}、{t,z},再对集合{t,z}、{t,x}、{t,y}来挖掘对应的条件树,知道条件树中没有元素为止。
Python代码如下:
class treeNode:
def __init__(self, nameValue, numOccur, parentNode):
self.name = nameValue
self.count = numOccur
self.nodeLink = None
self.parent = parentNode # needs to be updated
self.children = {}
def inc(self, numOccur):
self.count += numOccur
def disp(self, ind=1):
print(' '*ind, self.name, ' ', self.count)
for child in self.children.values():
child.disp(ind+1)
# 构建树节点及子节点
# rootNode = treeNode('pyramid', 9, None)
# rootNode.disp()
# print()
# rootNode.children['eye'] = treeNode('eye', 13, None)
# rootNode.children['phoenix'] = treeNode('phoenix', 3, None)
# rootNode.disp()
def createTree(dataSet, minSup=1): # create FP-tree from dataset but don't mine
headerTable = {}
for trans in dataSet: # first pass counts frequency of occurance
for item in trans:
headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
for k in list(headerTable.keys()): # remove items not meeting minSup
if int(headerTable[k]) < minSup:
del(headerTable[k])
# headerTable={'z': 5, 'r': 3, 'x': 4, 't': 3, 's': 3, 'y': 3}
freqItemSet = set(headerTable.keys())
if len(freqItemSet) == 0: return None, None # if no items meet min support -->get out
for k in headerTable:
headerTable[k] = [headerTable[k], None] # reformat headerTable to use Node link
# headerTable={'z': [5, None], 'r': [3, None], 'y': [3, None], 't': [3, None], 's': [3, None], 'x': [4, None]}
retTree = treeNode('Null Set', 1, None) # create tree
for tranSet, count in dataSet.items(): # go through dataset 2nd time
localD = {}
for item in tranSet:
if item in freqItemSet:
localD[item] = headerTable[item][0]
# localD 筛选每行数据,只保留频繁的数据点['r', 'z', 'h', 'j', 'p']>['z':5, 'r':3]
if len(localD) > 0:
orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)]
# print(orderedItems)
# orderedItems只保留keys(),例如['z':5, 'r':3]>['z', 'r']
updateTree(orderedItems, retTree, headerTable, count) # populate tree with ordered freq itemset
return retTree, headerTable # return tree and header table
def updateTree(items, inTree, headerTable, count):
if items[0] in inTree.children: # 如果树中已存在现有元素,则增加现有元素的值
inTree.children[items[0]].inc(count)
else: # 如果现有元素不存在,则向树添加一个分支
inTree.children[items[0]] = treeNode(items[0], count, inTree)
if headerTable[items[0]][1] == None: # update header table
headerTable[items[0]][1] = inTree.children[items[0]]
else:
updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
if len(items) > 1: # 元素个数大于1时继续迭代过程
updateTree(items[1::], inTree.children[items[0]], headerTable, count)
def updateHeader(nodeToTest, targetNode): # this version does not use recursion
while (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list!
nodeToTest = nodeToTest.nodeLink
nodeToTest.nodeLink = targetNode
def loadSimpDat():
simpDat = [['r', 'z', 'h', 'j', 'p'],
['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
['z'],
['r', 'x', 'n', 'o', 's'],
['y', 'r', 'x', 'z', 'q', 't', 'p'],
['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
return simpDat
def createInitSet(dataSet):
retDict = {}
for trans in dataSet:
retDict[frozenset(trans)] = 1
return retDict
# 测试FP-growth算法
minSup = 3
simpDat = loadSimpDat()
initSet = createInitSet(simpDat)
myFPtree, myHeaderTab = createTree(initSet, minSup)
myFPtree.disp()
def ascendTree(leafNode, prefixPath): #ascends from leaf node to root
if leafNode.parent != None:
prefixPath.append(leafNode.name)
ascendTree(leafNode.parent, prefixPath)
def findPrefixPath(basePat, treeNode): #treeNode comes from header table
condPats = {}
while treeNode != None:
prefixPath = []
ascendTree(treeNode, prefixPath)
if len(prefixPath) > 1:
condPats[frozenset(prefixPath[1:])] = treeNode.count
treeNode = treeNode.nodeLink
# print(condPats)
return condPats
def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1][0])]#(sort header table)
print(bigL)
for basePat in bigL: #start from bottom of header table
newFreqSet = preFix.copy()
newFreqSet.add(basePat)
# print(newFreqSet)
#print 'finalFrequent Item: ',newFreqSet #append to set
freqItemList.append(newFreqSet)
print(freqItemList)
condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
print(condPattBases)
#print 'condPattBases :',basePat, condPattBases
#2. construct cond FP-tree from cond. pattern base
myCondTree, myHead = createTree(condPattBases, minSup)
print('head from conditional tree: ', myHead)
#print 'head from conditional tree: ', myHead
if myHead != None: #3. mine cond. FP-tree
#print 'conditional tree for: ',newFreqSet
#myCondTree.disp(1)
myCondTree.disp()
mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)
myFreqList = []
mineTree(myFPtree, myHeaderTab, minSup, set([]), myFreqList)
print(myFreqList)