雷达辐射源调制信号仿真

雷达辐射源调制信号仿真

说明：通过Matlab进行单载频（CW），线性调频（LFM）、非线性调频（NLFM）、二相编码（BPSK）、四相编码（QPSK）、二频编码（BFSK）、四频编码（QFSK）七种雷达脉内调制信号的方仿真。

环境：Matlab

雷达辐射源调制信号仿真（代码）

---

1.单载频信号

单载频常规脉冲信号其频率和相位不随时间的变化而变化是最基本的雷达信号，其时宽带宽积约为1。数学表达式如下：
$$s\left(t\right)=u\left(t\right)e^{j(2\pi f_{0}t+{\phi }_0)}$$
其中$u\left(t\right)$为常规矩形脉冲信号的归一化包络：
$$\{\begin{array}{l}\frac{1}{\sqrt{T}},-\frac{T}{2}<t<\frac{T}{2}\\ 0,\end{array}$$

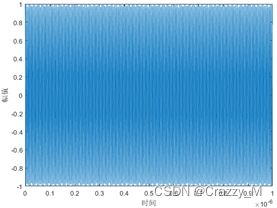
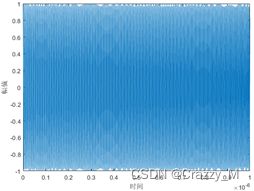
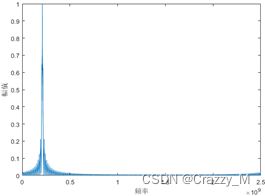
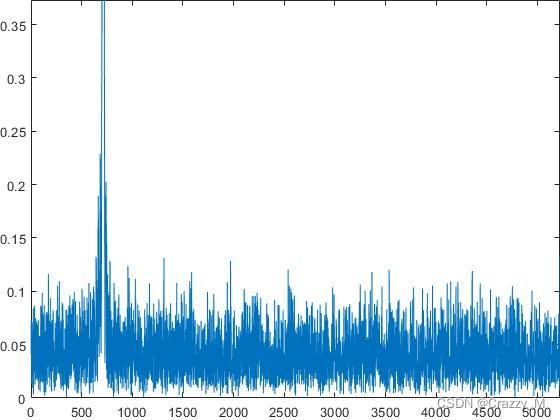
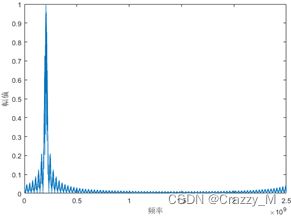
$T$为单载频脉宽， $f_0$为载频， ${\phi }_0$为初相。单载频脉冲信号的时域、频域波形如下图所示：

时域：

频域：

频域加噪声：

从上图中可以看出，单载频脉冲信号是频率和相位不随时间变换的信号，其频谱只有单一的频点。

2.线性调频信号

基于自适应滤波器理论的线性调频（LFM）信号，在信号有较大的多普勒频移条件下，匹配滤波器仍能起到脉压的作用，其数学表达式如下：

$$s(t)=u(t)e^{j(2\pi f_{0}t+{\phi }_0)}$$
其中 $u(t)$为线性调频矩形脉冲的复包络：

$$u(t)=\frac{1}{\sqrt{T}}rect(\frac{t}{T})e^{j\pi \mu t^2},rect(\frac{t}{T})=\{\begin{array}{l}1,|t|\le T/2\\ 0,|t|>T/2\end{array}$$

$T$为线性调频脉冲信号的脉宽， $f_0$为载波频率， ${\phi }_0$为初始相位， $\mu =B/T$为调频斜率， $B$为频偏，即调频带宽。线性调频脉冲信号时域、频域图如下所示：

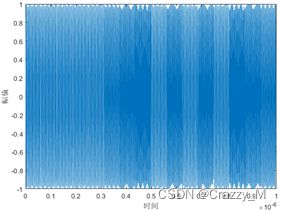
时域：

频域：

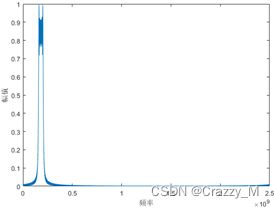
频域加噪声：

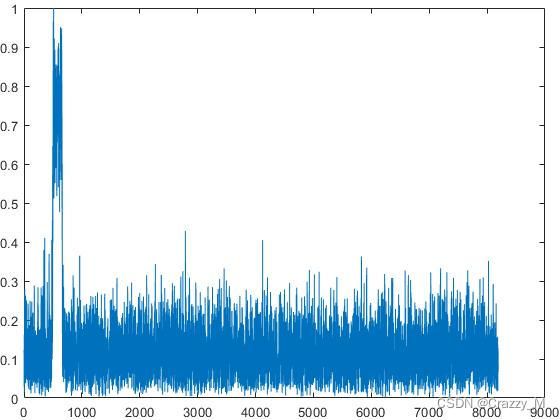
信号密集程度随t发生变化，即信号的频率随时间发生线性变化，从频域图中看出频谱也是按线性函数变化。

3.非线性调频信号

线性调频中对现代雷达大时宽带宽的要求可通过脉压的手段进行调节，却依然存在主副瓣比偏低的现象。在此之后又衍生出非线性调频技术，以种类全面和应用范围广著称，本文采用逗留相位原理进行近似求解的非线性调频信号，首先选择一个hamming窗，其表达式为：
$$W(f)=\{\begin{array}{l}0.54-0.46\cos (\frac{2\pi f}{B}),|f|\le \frac{B}{2}\\ 0,|f|>\frac{B}{2}\end{array}$$

对给定的函数 $W(f)$推导出群函数$T(f)$ ：
$$T(f)=K_1{\int }_{-\infty }^{f}W(x)dx,-\frac{B}{2}\le f\le \frac{B}{2}$$

其中$K_1$为常系数，可以通过具体的时间延迟和频率偏移决定，通过迭代数值计算方法计算出 $T(f)$的反函数$f(t)$ ：
$$f(t)=T^{-1}(f),0\le t\le T$$

即调频函数，对函数$f(t)$进行积分得到相位$\theta (t)$ ：
$$\theta (t)=2\pi {\int }_0^{t}f(x)dx,0\le t\le T$$
最终得到非线性调频信号：
$$\begin{array}{l}s(t)=Arect(\frac{t}{\sqrt{T}})e^{j[2\pi f_{0}t+\theta (t)+{\phi }_0]},0\le t\le T\\ Arect(\frac{t}{\sqrt{T}})=\{\begin{array}{l}1,|t|\le T/2\\ 0,|t|>T/2\end{array}\end{array}$$

其中$T$为非线性调频脉冲信号的脉宽， $f_0$为载率， ${\phi }_0$为信号初相， $\theta (t)$为非线性调频信号。非线性调频时域、频域图如下：

时域：

频域：

频域加噪声：

非线性调频信号时域图信号的密集程度呈非线性变化，在频域图中频谱也是呈非线性变化。

4.二相编码信号

相位编码信号具有在小时宽带宽积条件下有良好的主旁瓣比的优势，因此相位编码调制方式被广泛应用于现代雷达。相位编码脉冲信号，通过规定的序列对内部子脉冲相位进行编码，各个子脉冲之间紧密相连。二相编码信号子脉冲之间相位差只有0和π两个取值，常用的编码有巴克码、M序列和L序列码等。其数学表达式如下：
$$s(t)=u(t)e^{j(2\pi f_0+{\phi }_0)}$$
其中：
$$u(t)=\{\begin{array}{l}\frac{1}{\sqrt{P}}\sum _{K=0}^{P-1}{\mathrm{c}}_{K}v(t-KT),0<t<PT\\ 0,\end{array}$$

为二相编码矩形脉冲的复包络， $v(t)$为内部脉冲函数， $T$为内部脉宽， $P$为码元的长度， $PT$为信号的时长，二相编码信号对应序列取值为{ $c_K=1,-1$}。本文中二相编码所使用的编码序列为具有理想非周期自相关函数特性的巴克码。二相编码信号的时域、频域如下所示：

时域：

频域：

频域加噪声：

从以上二相编码信号时域图中可以看出，在两个子脉冲之间相位按照编码序列规律出现了0和π的偏移，信号密集程度没有发生改变，即频率没有发生变化。在二相编码信号的频域图中频谱表现为为单一的频点。

5.四相编码信号

四相编码信号表现为，子脉冲之间相位相差0，$\pi /2$ ，π 以及 $3\pi /2$四种可能。因为目前已知的巴克码序列的长度有限，所能提供的最优副瓣衰减为-22.2dB，为了满足脉内调制的需求，四相编码信号常采用泰勒（Taylor），法兰克（Frank）多相码等，本文采用了Frank码构造四相编码信号。其数学表达式如下：
$$s(t)=u(t)e^{j(2\pi f_0+{\phi }_0)}$$

其中：
$$u(t)=\{\begin{array}{l}\frac{1}{\sqrt{P}}\sum _{K=0}^{P-1}{\mathrm{c}}_{K}v(t-KT),0<t<PT\\ 0,\end{array}$$

为四相编码矩形脉冲的复包络， $v(t)$为内部脉冲函数， $T$为内部脉宽， $P$为码元长度， $PT$为信号的时长，四相编码信号对应序列取值为{$c_K=1,j,-1,-j$}。四相编码信号的时域、频域如下所示：

时域：

频域：

频域加噪声：

从以上四相编码信号时域图中可以看出，在某两个子脉冲之间相位按照编码序列规律分别出现了0，$\pi /2$ ，π 以及 $3\pi /2$的偏移，信号密集程度没有发生改变，即频率没有发生变化。在四相编码信号的频域图中频谱表现为为单一的频点。

6.二频编码信号

频率编码信号也广泛应用于现代雷达，通过编码序列将矩形脉冲内的子脉冲进行编码，表现为内部子脉冲信号频率在规定的频率集合{$f_1...f_M$ }中变化，此类编码的信号具有良好的距离分辨率和瞬时带宽。二频编码的数学表达式如下：
$$s(t)=u(t)e^{j(2\pi f_i+2\pi f_0+{\phi }_0)}$$

其中$u(t)$
$$\begin{array}{l}u(t)=\sum _{i=0}^{N_c-1}Arect[t-i\Delta L,\Delta L]\\ Arect[t-i\Delta L,\Delta L]=\{\begin{array}{l}1,0\le n\Delta T\le \Delta L\\ 0\end{array}\end{array}$$
为二频编码脉冲信号的复包络， $f_0$为载波频率， $f_i$为频率码组， ${\phi }_0$为初始相位， $\Delta L$为子码宽度。二频编码的频率码组只有{ $f_1,f_2$}两种取值，即在矩形脉冲内部，子脉冲频率根据编码序列，分别取值频率码组中的频率。二频编码信号的时域、频域如下所示：

时域：

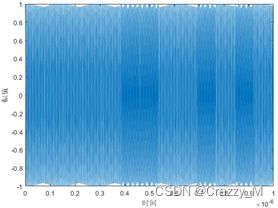
频域：

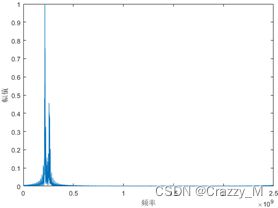
频域加噪声：

从以上二频编码时域图可以看出，信号的密集程度即信号的频率按照编码规律在{$f_1,f_2$}中变化。在频域图中频谱表现为两个频点。

7.四频编码信号

四频编码信号的数学表达式如下：

$s(t)=u(t)e^{j(2\pi f_i+2\pi f_0+{\phi }_0)}$

其中 $u(t)$：

$\begin{array}{l}u(t)=\sum _{i=0}^{N_c-1}Arect[t-i\Delta L,\Delta L]\\ Arect[t-i\Delta L,\Delta L]=\{\begin{array}{l}1,0\le n\Delta T\le \Delta L\\ 0\end{array}\end{array}$

为四频编码脉冲信号的复包络， $f_0$为载波频率， $f_i$为频率码组， ${\phi }_0$为初始相位， $\Delta L$为子码宽度。四频编码的频率码组有{ $f_1,f_2,f_3,f_4$}四种取值，即在矩形脉冲内部，子脉冲频率根据Frank编码序列分别取值频率码组中的频率。四频编码信号的时域、频域如下所示：

时域：

频域：

频域加噪：

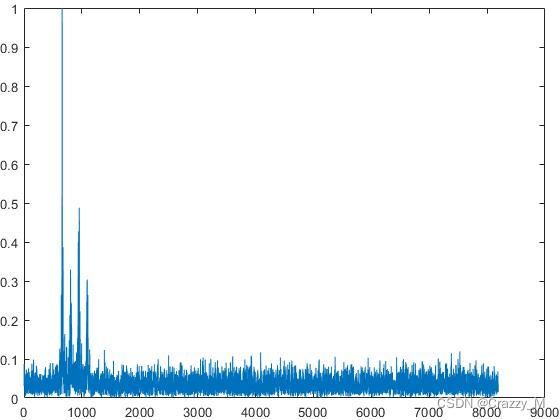
从以上四频编码时域图可以看出，信号的密集程度即信号的频率按照编码规律在{$f_1,f_2,f_3,f_4$ }中变化。在频域图中频谱表现为四个频点。