【OpenCV C++&Python】（四）图像阈值处理

图像阈值处理

Python

简单阈值处理

OpenCV的cv.threshold用于简单阈值处理，它的第一个参数是灰度源图像src；第二个参数是阈值thresh；第三个参数是赋值给超过阈值的像素的最大值maxval；第四个参数则是阈值处理的类型：

cv.threshold返回两个输出。第一个是使用的阈值，第二个输出是阈值图像dst。下面比较不同类型的阈值处理方法：

import cv2 as cv
from matplotlib import pyplot as plt
import numpy as np

img = cv.imread('threshold.jpg', 0)
ret, thresh1 = cv.threshold(img, 127, 255, cv.THRESH_BINARY)
ret, thresh2 = cv.threshold(img, 127, 255, cv.THRESH_BINARY_INV)
ret, thresh3 = cv.threshold(img, 127, 255, cv.THRESH_TRUNC)
ret, thresh4 = cv.threshold(img, 127, 255, cv.THRESH_TOZERO)
ret, thresh5 = cv.threshold(img, 127, 255, cv.THRESH_TOZERO_INV)
titles = ['Original Image', 'BINARY', 'BINARY_INV', 'TRUNC', 'TOZERO', 'TOZERO_INV']
images = [img, thresh1, thresh2, thresh3, thresh4, thresh5]
for i in range(6):
    plt.subplot(2, 3, i + 1), plt.imshow(images[i], 'gray')
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

自适应阈值处理

简单阈值处理在图像全局都使用同一个阈值，如果图像在不同区域有不同的照明条件，这可能就不适用了。在这种情况下，自适应阈值处理更适合。自适应阈值处理根据像素周围的一个小区域来确定阈值。可以使用OpenCV的cv.adaptiveThreshold实现这个功能。

cv.adaptiveThreshold的第一个参数是灰度源图像src；第二个参数是赋值给超过阈值的像素的最大值maxval；

第三个参数adaptiveMethod决定如何计算阈值:

• cv.ADAPTIVE_THRESH_MEAN_C：阈值是邻域内像素的平均值减去常数C。

• cv.ADAPTIVE_THRESH_GAUSSIAN_C：阈值是邻域内像素的高斯加权和减去常数C。

第四个参数则是阈值处理的类型；第五个参数 blockSize决定邻域区域的大小；第六个参数是常数C。

下面对比一下简单阈值处理和自适应阈值处理：

import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('adaptiveThreshold.jpg', 0)
ret, th1 = cv.threshold(img, 127, 255, cv.THRESH_BINARY)
th2 = cv.adaptiveThreshold(img, 255, cv.ADAPTIVE_THRESH_MEAN_C, cv.THRESH_BINARY, 11, 2)
th3 = cv.adaptiveThreshold(img, 255, cv.ADAPTIVE_THRESH_GAUSSIAN_C, cv.THRESH_BINARY, 11, 2)

titles = ['Original Image', 'BINARY(v=127)',
          'ADAPTIVE_THRESH_MEAN_C', 'ADAPTIVE_THRESH_GAUSSIAN_C']
images = [img, th1, th2, th3]
for i in range(4):
    plt.subplot(2, 2, i + 1), plt.imshow(images[i], 'gray')
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

大津(Otsu)法

在普通阈值处理中，我们需要指定阈值。大津法则能够从图像直方图中自动确定一个最优的全局阈值，即使用大津法不用人工挑选阈值。

大津法确定阈值的方法是找到一个阈值$T$，使类间方差最大或类内方差最小。设图像像素数为$N$，灰度范围为$[0,L]$。对应灰度级$i$的像素数为$n_i$，灰度级$i$的频率为：

$$p_i=\frac{n_i}{N},i=0,1,2,\cdots ,L-1$$

总和为1：
$$\sum _{i=0}^{L-1}{p}_i=1$$

把图像中像素按灰度值用阈值$T$分成两类$C_0$和$C_1$，$C_0$由灰度值在$[0,T]$之间的像素组成，$C_1$由灰度值在$[T+1,L-1]$之间的像素组成。整幅图像的均值为：
$$\mu =\sum _{i=0}^{L-1}i{p}_i$$

令
$$w_0(T)=\sum _{i=0}^T{p}_i$$

$$w_1(T)=\sum _{i=T+1}^{L-1}{p}_i=1-w_0$$

则$C_0$和$C_1$的均值为：

$${\mu }_0(T)=\sum _{i=0}^T\frac{i{p}_i}{w_0(T)}$$

$${\mu }_1(T)=\sum _{i=T+1}^{L-1}\frac{i{p}_i}{w_1(T)}$$

由上面式子可得：

$$\mu =w_0(T){\mu }_0(T)+w_1(T){\mu }_1(T)$$

类内方差（within-class variance） 定义为：

$${\sigma }_w^2(T)=w_0(T){\sigma }_0^2(T)+w_1(T){\sigma }_1^2(T)$$

反映每一类样本方差的大小。（值越小，各类的样本越集中，越好分割）

类间方差（between-class variance） 定义为：

$${\sigma }_B^2(T)=w_0(T){\left({\mu }_0(T)-\mu \right)}^2+w_1(T){\left({\mu }_1(T)-\mu \right)}^2$$

相当于以每一类的均值作为该类的代表值，以总体均值为均值计算方差。类间方差反映阈值两侧数据之间的差异程度。（值越大，类别越明显，越好分割）

由$D(X)=E(X^2)-E^2(X)$，得到：

$${\sigma }_0^2(T)=\sum _{i=0}^T\frac{p_i{i}^2}{w_0(T)}-{\mu }_0^2(T)$$

$${\sigma }_1^2(T)=\sum _{i=T+1}^{L-1}\frac{p_i{i}^2}{w_1(T)}-{\mu }_1^2(T)$$

$${\sigma }^2=\sum _{i=0}^{L-1}{p}_i{i}^2-{\mu }^2,为常数$$

再由：

$$\begin{array}{rl}{\sigma }_B^2(T)& =w_0{\left({\mu }_0-\mu \right)}^2+w_1{\left({\mu }_1-\mu \right)}^2\\ & ={\mu }^2\left(w_0+w_1\right)+w_0{\mu }_0^2-2w_0{\mu }_0\mu +w_1{\mu }_1^2-2w_1{\mu }_1\mu \\ & ={\mu }^2+w_0{\mu }_0^2+w_1{\mu }_1^2-2w_0{\mu }_0\mu -2w_1{\mu }_1\mu \leftarrow (由w_0+w_1=1)\\ & ={\mu }^2+w_0{\mu }_0^2+w_1{\mu }_1^2-2\mu (w_0{\mu }_0+w_1{\mu }_1)\\ & =w_0{\mu }_0^2+w_1{\mu }_1^2-(w_0{\mu }_0+w_1{\mu }_1{)}^2\leftarrow (由\mu =w_0{\mu }_0+w_1{\mu }_1)\\ & =w_0{\mu }_0^2+w_1{\mu }_1^2-w_0^2{\mu }_0^2-w_1^2{\mu }_1^2-2w_0{w}_1{\mu }_0{\mu }_1\\ & =w_0{\mu }_0^2(1-w_0)+w_1{\mu }_1^2(1-w_1)-2w_0{w}_1{\mu }_0{\mu }_1\\ & =w_0{w}_1{\mu }_0^2+w_0{w}_1{\mu }_1^2-2w_0{w}_1{\mu }_0{\mu }_1\leftarrow (由w_0+w_1=1)\\ & =w_0{w}_1{\left({\mu }_0-{\mu }_1\right)}^2\end{array}$$

得到：

$$\begin{array}{rl}{\sigma }_w^2(T)+{\sigma }_b^2(T)& =w_0{\sigma }_0^2(T)+w_1{\sigma }_1^2(T)+w_0{w}_1{\left(u_0-u_1\right)}^2\\ & =w_0(\sum _{i=0}^T\frac{p_i{i}^2}{w_0}-{\mu }_0^2)+w_1(\sum _{i=T+1}^{L-1}\frac{p_i{i}^2}{w_1}-{\mu }_1^2)+w_0{w}_1{\left(u_0-u_1\right)}^2\\ & =\sum _{i=0}^T{p}_i{i}^2-w_0{\mu }_0^2+\sum _{i=T+1}^{L-1}{p}_i{i}^2-w_1{\mu }_1^2+w_0{w}_1{\left({\mu }_0-{\mu }_1\right)}^2\\ & =\sum _{i=0}^{L-1}{p}_i{i}^2-w_0^2{\mu }_0^2-w_1^2{\mu }_1^2-2w_0{w}_1{\mu }_0{\mu }_1\\ & =\sum _{i=0}^{L-1}{p}_i{i}^2-(w_0{u}_0+w_1{u}_1{)}^2\\ & =\sum _{i=0}^{L-1}{p}_i{i}^2-{\mu }^2\\ & ={\sigma }^2\end{array}$$

即类内方差与类间方差之和为定值，最大化类间方差与最小化类内方差等价。

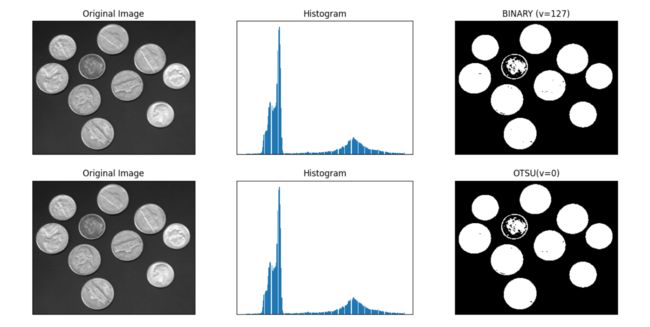
使用cv.threshold()函数，阈值处理的类型可以任意选择，THRESH_OTSU作为一个额外的flag即可使用大津法。下面以一个直方图包含两个峰的图像(双峰图像)为例：

import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('coins.png', 0)
# 普通二值化
ret1, th1 = cv.threshold(img, 127, 255, cv.THRESH_BINARY)
# Otsu法二值化
ret2, th2 = cv.threshold(img, 0, 255, cv.THRESH_BINARY + cv.THRESH_OTSU)  # 随便给个0为阈值

images = [img, [], th1,
          img, [], th2]
titles = ['Original Image', 'Histogram', 'BINARY (v=127)',
          'Original Image', 'Histogram', 'OTSU(v=0)']
for i in range(2):
    plt.subplot(2, 3, i * 3 + 1), plt.imshow(images[i * 3], 'gray')
    plt.title(titles[i * 3]), plt.xticks([]), plt.yticks([])
    plt.subplot(2, 3, i * 3 + 2), plt.hist(images[i * 3].ravel(), 256)
    plt.title(titles[i * 3 + 1]), plt.xticks([]), plt.yticks([])
    plt.subplot(2, 3, i * 3 + 3), plt.imshow(images[i * 3 + 2], 'gray')
    plt.title(titles[i * 3 + 2]), plt.xticks([]), plt.yticks([])
plt.show()

大津法无需人工指定阈值即可达到较为理想的效果。

C++

简单阈值处理

#include 
using namespace cv;
int main()
{
	Mat img = imread("threshold.jpg",0);
	Mat thresh1, thresh2, thresh3, thresh4, thresh5;
	
	threshold(img, thresh1, 127, 255, THRESH_BINARY);
	threshold(img, thresh2, 127, 255, THRESH_BINARY_INV);
	threshold(img, thresh3, 127, 255, THRESH_TRUNC);
	threshold(img, thresh4, 127, 255, THRESH_TOZERO);
	threshold(img, thresh5, 127, 255, THRESH_TOZERO_INV);

	imshow("Original Image", img);
	imshow("BINARY", thresh1);
	imshow("BINARY_INV", thresh2);
	imshow("TRUNC", thresh3);
	imshow("TOZERO", thresh4);
	imshow("TOZERO_INV", thresh5);
	waitKey(0);
	return 0;
}

自适应阈值处理

#include 
using namespace cv;
int main()
{
	Mat img = imread("adaptiveThreshold.jpg",0);
	Mat thresh1, thresh2, thresh3;
	threshold(img, thresh1, 127, 255, THRESH_BINARY);
	adaptiveThreshold(img, thresh2,255, ADAPTIVE_THRESH_MEAN_C, THRESH_BINARY, 11, 2);
	adaptiveThreshold(img, thresh3,255, ADAPTIVE_THRESH_GAUSSIAN_C, THRESH_BINARY, 11, 2);

	imshow("Original Image", img);
	imshow("BINARY", thresh1);
	imshow("ADAPTIVE_THRESH_MEAN_C", thresh2);
	imshow("ADAPTIVE_THRESH_GAUSSIAN_C", thresh3);
	waitKey(0);
	return 0;
}

大津(Otsu)法

#include 
using namespace cv;
int main()
{
	Mat img = imread("coins.png",0);
	Mat thresh1, thresh2;
	threshold(img, thresh1, 127, 255, THRESH_BINARY);
	threshold(img, thresh2, 0, 255, THRESH_BINARY + THRESH_OTSU);

	imshow("Original Image", img);
	imshow("BINARY", thresh1);
	imshow("OTSU", thresh2);
	waitKey(0);
	return 0;
}

代码：
https://gitee.com/BinaryAI/open-cv-c–and-python

参考：

[1]https://docs.opencv.org/4.6.0/

[2]https://zhuanlan.zhihu.com/p/384457101

[3]数字图像处理（MATLAB版）（第2版）,张德丰, 人民邮电出版社