注意力、自注意力和多头注意力
动手学深度学习笔记
- 一、注意力评分函数
-
- 1.masked softmax
- 2.加性注意力
- 3.缩放点积注意力
- 二、使用注意力机制的Seq2Seq
-
- 1.重新定义上下文向量
- 2.定义注意力解码器
- 三、多头注意力
-
- 1.模型
- 2.代码实现
- 四、自注意力和位置编码
-
- 1.自注意力
- 2.位置编码
一、注意力评分函数
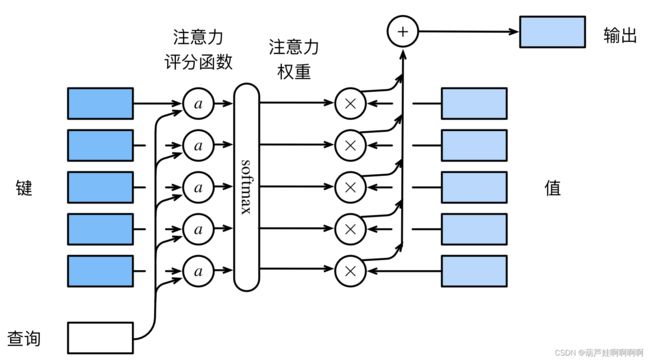
把注意力函数的输出结果输入到softmax中进行运算,将得到与键对应的值的概率分布(即注意力权重)。 最后,注意力汇聚的输出就是基于这些注意力权重的值的加权和。
f ( q , ( k 1 , v 1 ) , … , ( k m , v m ) ) = ∑ i = 1 m α ( q , k i ) v i ∈ R v α ( q , k i ) = s o f t m a x ( a ( q , k i ) ) = exp ( a ( q , k i ) ) ∑ j = 1 m exp ( a ( q , k j ) ) ∈ R f(\mathbf{q}, (\mathbf{k}_1, \mathbf{v}_1), \ldots, (\mathbf{k}_m, \mathbf{v}_m)) = \sum_{i=1}^m \alpha(\mathbf{q}, \mathbf{k}_i) \mathbf{v}_i \in \mathbb{R}^v\\ \alpha(\mathbf{q}, \mathbf{k}_i)=\mathrm{softmax}(a(\mathbf{q}, \mathbf{k}_i)) = \frac{\exp(a(\mathbf{q}, \mathbf{k}_i))}{\sum_{j=1}^m \exp(a(\mathbf{q}, \mathbf{k}_j))} \in \mathbb{R} f(q,(k1,v1),…,(km,vm))=i=1∑mα(q,ki)vi∈Rvα(q,ki)=softmax(a(q,ki))=∑j=1mexp(a(q,kj))exp(a(q,ki))∈R
选择不同的注意力评分函数 a a a 会导致不同的注意力权重值。
1.masked softmax
softmax操作用于输出一个概率分布作为注意力权重。但是,有时候某些文本序列被填充了没有意义的特殊词元,如’
def masked_softmax(X, valid_lens):
"""通过在最后一个轴上掩蔽元素来执行softmax操作"""
# X:3D张量,valid_lens:1D或2D张量
if valid_lens is None:
return F.softmax(X, dim = -1)
shape = X.shape
if valid_lens.dim() == 1:
valid_lens = torch.repeat_interleave(valid_lens, shape[1])
else:
valid_lens = valid_lens.reshape(-1)
# 最后一轴上被掩蔽的元素使用一个非常大的负值替换,从而其softmax输出为0
X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens, value=-1e6)
return F.softmax(X.reshape(shape), dim=-1)
# masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))
masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]]))
2.加性注意力
当查询和键是不同长度的矢量时,一般使用加性注意力作为评分函数。给定查询 q ∈ R q \mathbf{q} \in \mathbb{R}^q q∈Rq和键 k ∈ R k \mathbf{k} \in \mathbb{R}^k k∈Rk,加性注意力(additive attention)的评分函数为:
a ( q , k ) = w v ⊤ tanh ( W q q + W k k ) ∈ R a(\mathbf q, \mathbf k) = \mathbf w_v^\top \text{tanh}(\mathbf W_q\mathbf q + \mathbf W_k \mathbf k) \in \mathbb{R} a(q,k)=wv⊤tanh(Wqq+Wkk)∈R
class AdditiveAttention(nn.Module):
"""加性注意力"""
def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
super(AdditiveAttention, self).__init__(**kwargs)
self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
self.w_v = nn.Linear(num_hiddens, 1, bias=False)
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values, valid_lens):
queries, keys = self.W_q(queries), self.W_k(keys)
# 维度扩展后,使用广播方式进行求和
# queries的形状:(batch_size,查询的个数,1,num_hidden)
# key的形状:(batch_size,1,“键-值”对的个数,num_hiddens)
features = queries.unsqueeze(2) + keys.unsqueeze(1)
features = torch.tanh(features)
# self.w_v仅有一个输出,因此从形状中移除最后那个维度。
# scores的形状:(batch_size,查询的个数,“键-值”对的个数)
scores = self.w_v(features).squeeze(-1)
self.attention_weights = masked_softmax(scores, valid_lens)
# values的形状:(batch_size,“键-值”对的个数,值的维度)
# 输出形状:(batch_size,查询的个数,值的维度)
return torch.bmm(self.dropout(self.attention_weights), values)
queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
# values的小批量,两个值矩阵是相同的
values = torch.arange(40,dtype=torch.float32).reshape(1,10,4).repeat(2,1,1)
valid_lens = torch.tensor([2, 6])
attention = AdditiveAttention(key_size=2, query_size=20, num_hiddens=8,
dropout=0.1)
attention.eval()
print(attention(queries, keys, values, valid_lens))
# valid_lens = torch.tensor([2, 6]),所以queries的attention权重分别有两个、六个
d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
xlabel='Keys', ylabel='Queries')
3.缩放点积注意力
上面的加性注意力评分函数计算效率不高,点积注意力计算效率更高,不过点积操作要求查询和键具有相同的长度 d d d。为确保无论向量长度如何,点积的方差在不考虑向量长度的情况下仍然是 1 1 1,于是有了缩放点积注意力(scaled dot-product attention)评分函数:
a ( q , k ) = q ⊤ k / d a(\mathbf q, \mathbf k) = \mathbf{q}^\top \mathbf{k} /\sqrt{d} a(q,k)=q⊤k/d
从向量扩展到矩阵,例如基于 n n n个查询和 m m m个键-值对计算注意力,其中查询和键的长度为 d d d,值的长度为 v v v。查询 Q ∈ R n × d \mathbf Q\in\mathbb R^{n\times d} Q∈Rn×d、键 K ∈ R m × d \mathbf K\in\mathbb R^{m\times d} K∈Rm×d和值 V ∈ R m × v \mathbf V\in\mathbb R^{m\times v} V∈Rm×v的缩放点积注意力是:
s o f t m a x ( Q K ⊤ d ) V ∈ R n × v \mathrm{softmax}\left(\frac{\mathbf Q \mathbf K^\top }{\sqrt{d}}\right) \mathbf V \in \mathbb{R}^{n\times v} softmax(dQK⊤)V∈Rn×v
class DotProductAttention(nn.Module):
"""缩放点积注意力"""
def __init__(self, dropout, **kwargs):
super(DotProductAttention, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout)
# queries的形状:(batch_size,查询的个数,d)
# keys的形状:(batch_size,“键-值”对的个数,d)
# values的形状:(batch_size,“键-值”对的个数,值的维度)
# valid_lens的形状:(batch_size,)或者(batch_size,查询的个数)
def forward(self, queries, keys, values, valid_lens=None):
d = queries.shape[-1]
scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
self.attention_weights = masked_softmax(scores, valid_lens)
return torch.bmm(self.dropout(self.attention_weights), values)
queries = torch.normal(0, 1, (2, 1, 2))
attention = DotProductAttention(dropout=0.5)
attention.eval()
print(attention(queries, keys, values, valid_lens))
d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
xlabel='Keys', ylabel='Queries')
二、使用注意力机制的Seq2Seq
在基于两个循环神经网络的编码器-解码器架构中,循环神经网络编码器将⻓度可变的序列转换为固定形状的上下文变量,然后循环神经网络解码器根据生成的词元和上下文变量按词元生成输出(目标)序列词元。在这个模型中,每个解码时间步都是使用编码相同的上下文变量,然而并非所有输入词元对解码某个词元都是有用的,为了解决这个问题可以考虑将注意力机制加入到模型解码过程中。
1.重新定义上下文向量

加入了注意力机制后,在任何解码时间步 t ′ t' t′, c t ′ \mathbf{c}_{t'} ct′都会替换 c \mathbf{c} c,也就是说,每个解码时间步的上下文向量将会动态改变,不再是一个固定的向量。
假设输入序列中有 T T T个token,解码时间步 t ′ t' t′的上下文变量是注意力的输出:
c t ′ = ∑ t = 1 T α ( s t ′ − 1 , h t ) h t \mathbf{c}_{t'} = \sum_{t=1}^T \alpha(\mathbf{s}_{t' - 1}, \mathbf{h}_t) \mathbf{h}_t ct′=t=1∑Tα(st′−1,ht)ht
其中,query是时间步 t ′ − 1 t' - 1 t′−1时的解码器隐状态 s t ′ − 1 \mathbf{s}_{t' - 1} st′−1,key和value相同,是编码器t时刻的隐状态 h t \mathbf{h}_t ht,注意力权重 α \alpha α是通过注意力打分函数计算的。
2.定义注意力解码器
class AttentionDecoder(d2l.Decoder):
"""带有注意力机制解码器的基本接口"""
def __init__(self, **kwargs):
super(AttentionDecoder, self).__init__(**kwargs)
@property
def attention_weights(self):
raise NotImplementedError
class Seq2SeqAttentionDecoder(AttentionDecoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqAttentionDecoder, self).__init__(**kwargs)
self.attention = d2l.AdditiveAttention(num_hiddens,
num_hiddens, num_hiddens, dropout)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.GRU(embed_size + num_hiddens, num_hiddens,
num_layers,dropout=dropout)
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, enc_valid_lens, *args):
# outputs的形状为(batch_size,num_steps,num_hiddens)
# hidden_state的形状为(num_layers,batch_size,num_hiddens)
outputs, hidden_state = enc_outputs
return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)
def forward(self, X, state):
# enc_outputs的形状为(batch_size,num_steps,num_hiddens)
# hidden_state的形状为(num_layers,batch_size,num_hiddens)
enc_outputs, hidden_state, enc_valid_lens = state
# 输出X的形状为(num_steps,batch_size,embed_size)
X = self.embedding(X).permute(1, 0, 2)
outputs, self._attention_weights = [], []
for x in X:
# query的形状为(batch_size,1,num_hiddens)
query = torch.unsqueeze(hidden_state[-1], dim=1)
# context的形状为(batch_size,1,num_hiddens)
context = self.attention(
query, enc_outputs, enc_outputs, enc_valid_lens)
# 在特征维度上连结
x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)
# 将x变形为(1,batch_size,embed_size+num_hiddens)
out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)
outputs.append(out)
self._attention_weights.append(self.attention.attention_weights)
# 全连接层变换后,outputs的形状为
# (num_steps,batch_size,vocab_size)
outputs = self.dense(torch.cat(outputs, dim=0))
return outputs.permute(1, 0, 2), [enc_outputs, hidden_state,
enc_valid_lens]
@property
def attention_weights(self):
return self._attention_weights
- 训练
embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1
batch_size, num_steps = 64, 10
lr, num_epochs, device = 0.005, 250, d2l.try_gpu()
train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = d2l.Seq2SeqEncoder(
len(src_vocab), embed_size, num_hiddens, num_layers, dropout)
decoder = Seq2SeqAttentionDecoder(
len(tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
net = d2l.EncoderDecoder(encoder, decoder)
d2l.train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)

- 用训练好的模型将几个英语句子翻译成法语,并计算BLEU分数。
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
translation, dec_attention_weight_seq = d2l.predict_seq2seq(
net, eng, src_vocab, tgt_vocab, num_steps, device, True)
print(f'{eng} => {translation}, ',
f'bleu {d2l.bleu(translation, fra, k=2):.3f}')
- 可视化注意力权重
attention_weights = torch.cat([step[0][0][0] for step in dec_attention_weight_seq],
0).reshape((1, 1, -1, num_steps))
# 加上一个包含序列结束词元
d2l.show_heatmaps(attention_weights[:, :, :, :len(engs[-1].split()) + 1].cpu(),
xlabel='Key positions', ylabel='Query positions')
三、多头注意力
有时我们希望模型可以基于相同的注意力机制学习到不同的行为,然后将不同的行为作为知识组合起来,捕获序列内各种范围的依赖关系(例如,短距离依赖和⻓距离依赖关系)。通过学习得到不同的投影矩阵来变换查询、键和值,然后将变换后的查询、键和值将并行地送到注意力汇聚层中。最后,将注意力汇聚的输出拼接在一起,并且通过另一个可以学习的线性投影进行变换,以产生最终输出。
说白了,就是一组Q、K和V,经过不同的全连接层,再经过注意力层,拼接注意力层的输出,再经过一个全连接层。
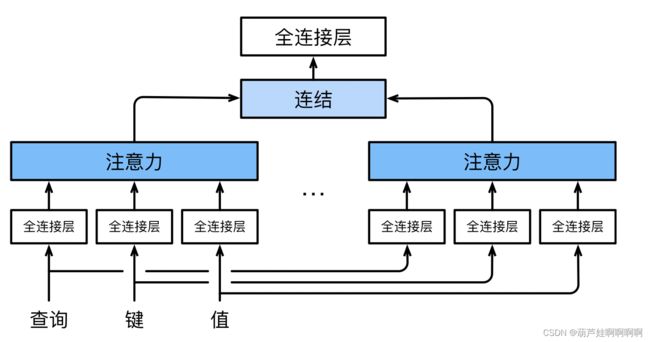
1.模型
给定查询 q ∈ R d q \mathbf{q} \in \mathbb{R}^{d_q} q∈Rdq、键 k ∈ R d k \mathbf{k} \in \mathbb{R}^{d_k} k∈Rdk和值 v ∈ R d v \mathbf{v} \in \mathbb{R}^{d_v} v∈Rdv,每个注意力头 h i \mathbf{h}_i hi( i = 1 , … , h i = 1, \ldots, h i=1,…,h)的计算方法为:
h i = f ( W i ( q ) q , W i ( k ) k , W i ( v ) v ) ∈ R p v \mathbf{h}_i = f(\mathbf W_i^{(q)}\mathbf q, \mathbf W_i^{(k)}\mathbf k,\mathbf W_i^{(v)}\mathbf v) \in \mathbb R^{p_v} hi=f(Wi(q)q,Wi(k)k,Wi(v)v)∈Rpv
其中, W i ( q ) ∈ R p q × d q \mathbf W_i^{(q)}\in\mathbb R^{p_q\times d_q} Wi(q)∈Rpq×dq、 W i ( k ) ∈ R p k × d k \mathbf W_i^{(k)}\in\mathbb R^{p_k\times d_k} Wi(k)∈Rpk×dk和 W i ( v ) ∈ R p v × d v \mathbf W_i^{(v)}\in\mathbb R^{p_v\times d_v} Wi(v)∈Rpv×dv是可学习的矩阵, f f f表示注意力汇聚的函数( f f f可以是加性注意力和缩放点积注意力)。
如上图所示,多头注意力的输出拼接后再经过一个线性转换:
W o [ h 1 ⋮ h h ] ∈ R p o \mathbf W_o \begin{bmatrix}\mathbf h_1\\\vdots\\\mathbf h_h\end{bmatrix} \in \mathbb{R}^{p_o} Wo⎣⎢⎡h1⋮hh⎦⎥⎤∈Rpo
其中 W o ∈ R p o × h p v \mathbf W_o\in\mathbb R^{p_o\times h p_v} Wo∈Rpo×hpv是可学习参数。
总结:
多头注意力融合了来自于多个注意力汇聚的不同知识,这些知识的不同来源于相同的查询、键和值的不同的子空间表示。
2.代码实现
令 p q = p k = p v = p o / h p_q = p_k = p_v = p_o / h pq=pk=pv=po/h,将查询、键和值的线性变换的输出数量设置为 p q h = p k h = p v h = p o p_q h = p_k h = p_v h = p_o pqh=pkh=pvh=po,则可以并行计算 h h h个头, p o p_o po是通过参数num_hiddens指定的。
class MultiHeadAttention(nn.Module):
"""多头注意力"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
num_heads, dropout, bias=False, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.num_heads = num_heads
self.attention = d2l.DotProductAttention(dropout)
self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)
def forward(self, queries, keys, values, valid_lens):
# q,k,v的形状:(batch_size,查询或者“键-值”对的个数,num_hiddens)
# valid_lens的形状:(batch_size,)或(batch_size,查询的个数)
# 变换后,输出的q,k,v的形状:
# (batch_size*num_heads,查询或者“键-值”对的个数,num_hiddens/num_heads)
queries = transpose_qkv(self.W_q(queries), self.num_heads)
keys = transpose_qkv(self.W_k(keys), self.num_heads)
values = transpose_qkv(self.W_v(values), self.num_heads)
if valid_lens is not None:
# 在轴0,将第一项(标量或者矢量)复制num_heads次,
# 然后如此复制第二项,然后诸如此类。
valid_lens = torch.repeat_interleave(
valid_lens, repeats=self.num_heads, dim=0)
# output:(batch_size*num_heads,查询的个数,num_hiddens/num_heads)
output = self.attention(queries, keys, values, valid_lens)
# output_concat:(batch_size,查询的个数,num_hiddens)
output_concat = transpose_output(output, self.num_heads)
return self.W_o(output_concat)
def transpose_qkv(X, num_heads):
"""为了多注意力头的并行计算而变换形状"""
# 输入X:(batch_size,查询或者“键-值”对的个数,num_hiddens)
X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
# 输出X:(batch_size,num_heads,查询或者“键-值”对的个数,num_hiddens/num_heads)
X = X.permute(0, 2, 1, 3)
# 输出形状:(batch_size*num_heads,查询或者“键-值”对的个数,num_hiddens/num_heads)
return X.reshape(-1, X.shape[2], X.shape[3])
def transpose_output(X, num_heads):
"""逆转transpose_qkv函数的操作"""
X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
X = X.permute(0, 2, 1, 3)
return X.reshape(X.shape[0], X.shape[1], -1)
四、自注意力和位置编码
1.自注意力
给定一个由词元组成的输入序列 x 1 , … , x n \mathbf{x}_1, \ldots, \mathbf{x}_n x1,…,xn,其中任意 x i ∈ R d \mathbf{x}_i \in \mathbb{R}^d xi∈Rd( 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n)。该序列的自注意力输出为一个长度相同的序列 y 1 , … , y n \mathbf{y}_1, \ldots, \mathbf{y}_n y1,…,yn,其中:
y i = f ( x i , ( x 1 , x 1 ) , … , ( x n , x n ) ) ∈ R d \mathbf{y}_i = f(\mathbf{x}_i, (\mathbf{x}_1, \mathbf{x}_1), \ldots, (\mathbf{x}_n, \mathbf{x}_n)) \in \mathbb{R}^d yi=f(xi,(x1,x1),…,(xn,xn))∈Rd也就是说,每个查询都会关注所有的键-值对并生成一个注意力输出。
由于查询、键和值来自同一组输入,因此被称为自注意力(self-attention)。
num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
num_hiddens, num_heads, 0.5)
attention.eval()
batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
attention(X, X, X, valid_lens).shape
2.位置编码
假设输入表示 X ∈ R n × d \mathbf{X} \in \mathbb{R}^{n \times d} X∈Rn×d包含一个序列中 n n n个词元的 d d d维嵌入表示。位置编码使用相同形状的位置嵌入矩阵 P ∈ R n × d \mathbf{P} \in \mathbb{R}^{n \times d} P∈Rn×d,输出 X + P \mathbf{X} + \mathbf{P} X+P,矩阵第 i i i行、第 2 j 2j 2j列和 2 j + 1 2j+1 2j+1列上的元素为:
p i , 2 j = sin ( i 1000 0 2 j / d ) , p i , 2 j + 1 = cos ( i 1000 0 2 j / d ) . \begin{aligned} p_{i, 2j} &= \sin\left(\frac{i}{10000^{2j/d}}\right),\\p_{i, 2j+1} &= \cos\left(\frac{i}{10000^{2j/d}}\right).\end{aligned} pi,2jpi,2j+1=sin(100002j/di),=cos(100002j/di).
class PositionalEncoding(nn.Module):
"""位置编码"""
def __init__(self, num_hiddens, dropout, max_len=1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
# 创建一个足够长的P
self.P = torch.zeros((1, max_len, num_hiddens))
X = torch.arange(max_len, dtype=torch.float32).reshape(
-1, 1) / torch.pow(10000, torch.arange(
0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
self.P[:, :, 0::2] = torch.sin(X)
self.P[:, :, 1::2] = torch.cos(X)
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
return self.dropout(X)
在位置嵌入矩阵 P \mathbf{P} P中,行代表词元在序列中的位置,列代表位置编码的不同维度。通过下图可以看出,不同行(词元)不同维度的值是不同的,也就是说可以代表不同的位置信息。
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])
