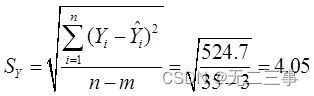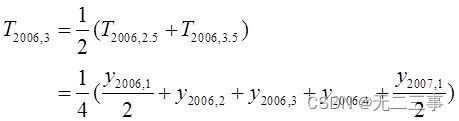贾俊平《统计学》第十三章时间序列分析和预测知识点总结及课后习题答案

目录

一、知识框架

二、练习题

---

一、知识框架

二、练习题

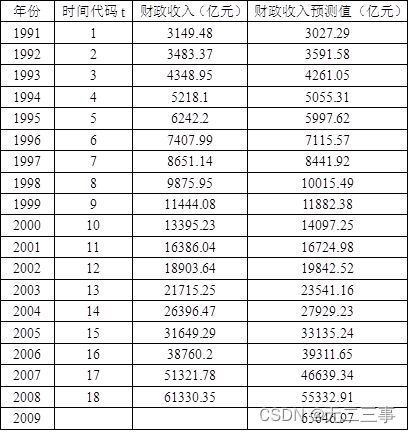
1是1991～2008年我国财政收入数据。采用指数曲线预测2009年的财政收入，并将实际值和预测值绘图进行比较。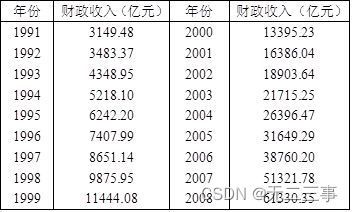

解：设指数曲线的趋势方程为Yt＝b0b1t，两端取对数得ln（Yt）＝ln（b0）＋tln（b1）。根据最小二乘法原理，求得ln（b1）＝0.1709，ln（b0）＝7.8445，对应指数曲线方程为Yt＝2551.6615×1.1864t。
将t＝1，2，…，18代入趋势方程得到各期的预测值，将t＝19代入趋势方程即可得到2009年财政收入的预测值。计算结果见

2表13-6是一家旅馆过去18个月的营业额数据。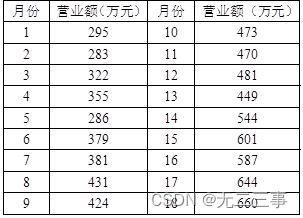

要求：
（1）用3期移动平均法预测第19个月的营业额。
（2）采用指数平滑法，分别用平滑系数α＝0.3，α＝0.4和α＝0.5预测各月的营业额，分析预测误差，说明用哪一个平滑系数预测更合适。
（3）建立一个趋势方程预测各月的营业额，计算出估计标准误差。

解：（1）第19个月的3期移动平均预测值为：
F19＝（587＋644＋660）/3＝630.33
（2）由Excel输出的指数平滑预测值，如表所示。

α＝0.3时的预测值为：F19＝0.3×660＋（1－0.3）×567.9＝595.5，误差平方＝87524.82
α＝0.4时的预测值为：F19＝0.4×660＋（1－0.4）×591.1＝618.7，误差平方＝50952.1
α＝0.5时的预测值为：F19＝0.5×660＋（1－0.5）×606.5＝633.3，误差平方＝50235.49比较各误差平方可知，α＝0.5更合适。
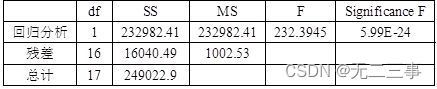
（3）根据最小二乘法，利用Excel输出的回归结果如表所示。

所以线性趋势方程为：Yt＝239.73＋21.9288t；估计标准误差SY＝31.6628。

3我国1964～1999年的纱产量数据，如表13-11所示（单位：万吨）。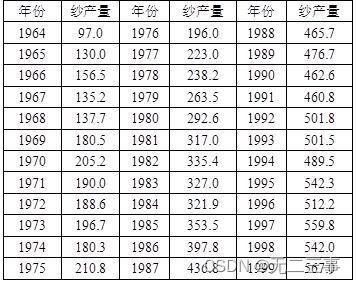

（1）绘制时间序列图描述其趋势。
（2）选择一条适合的趋势线拟合数据，并根据趋势线预测2000年的产量。

解：（1）绘制时间序列图，如图所示。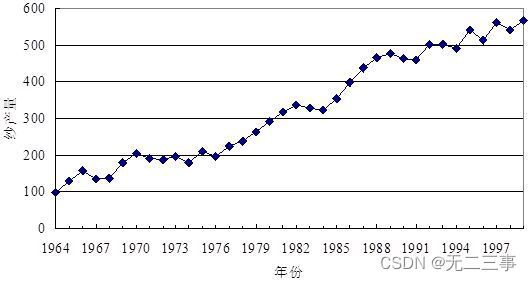

（2）从图中可以看出，纱产量具有明显的线性趋势。用Excel求得的线性趋势方程为：Yt＝69.5202＋13.9495t
所以2000年预测值为：Y37＝69.5202＋13.9495×37＝585.65（万吨）

4对表13-12的数据分别拟合线性趋势线Yt＝b0＋b1t、二阶曲线Yt＝b0＋b1t＋b2t2和三阶曲线Yt＝b0＋b1t＋b2t2＋b3t3，并对结果进行比较。

解：在求二阶曲线和三阶曲线时，首先将其线性化，然后用最小二乘法按线性回归进行求解。用Excel求得的趋势直线、二阶曲线和三阶曲线的系数，如表所示。

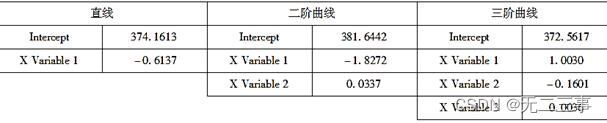
所以各趋势方程为：
线性趋势：Yt＝374.1613－0.6137t
二阶曲线：Yt＝381.6442－1.8272t＋0.0337t2三阶曲线：Yt＝372.5617＋1.0030t－0.1601t2＋0.0036t3
根据趋势方程求得的预测值和预测误差，如表所示。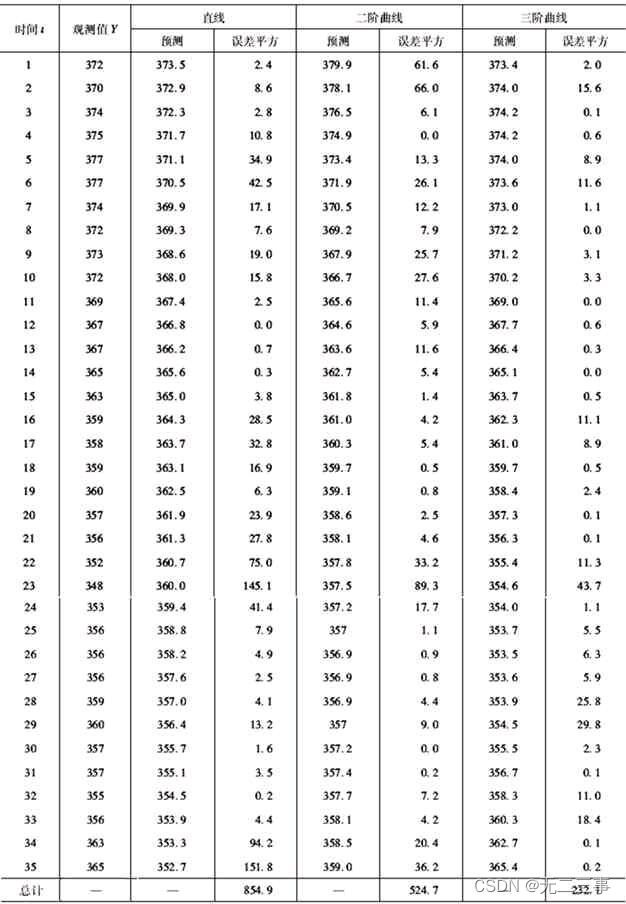

不同趋势线预测的标准误差分别为：
直线：

二阶曲线：

三阶曲线：

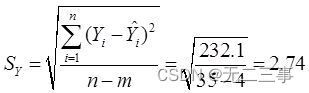
比较各预测误差可知，直线的误差最大，三阶曲线的误差最小。
从不同趋势方程的预测图（如图所示）也可以看出，三阶曲线与原序列的拟合最好。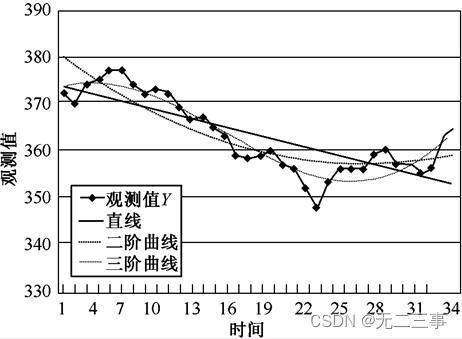

5一家贸易公司主要经营产品的外销业务，为了合理地组织货源，需要了解外销订单的变化状况。表是2011～2015年各月份的外销订单金额（单位：万元）。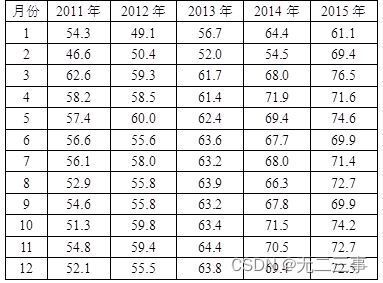

要求：
（1）根据各年的月份数据绘制趋势图，说明该时间序列的特点。
（2）要计算各月份的预测值，你认为应该采取什么方法？
（3）选择你认为合适的方法预测2016年1月份的外销订单金额。

解：（1）绘制趋势图，如图所示。

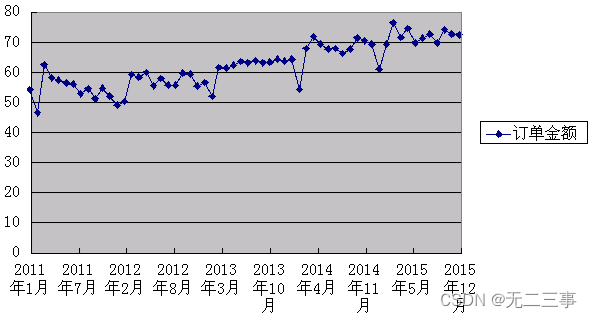
从趋势图可以看出，每一年的各月份数据没有趋势存在，但从2011～2015年的变化看，订单金额存在一定的线性趋势。
（2）由于是预测各月份的订单金额，因此采用移动平均法或指数平滑法比较合适。
（3）用Excel采用12项移动平均法预测的结果为：F2016/1＝71.4（万元）。
用Excel采用指数平滑法（α＝0.4）预测的预测结果为：F2016/1＝72.5（万元）。

6表13-16是一家大型百货公司最近几年各季度的销售额数据（单位：万元）。对这一时间序列的构成要素进行分解，计算季节指数，剔除季节变动，计算剔除季节变动后的趋势方程。

解：按季平均法计算季节指数，取移动平均项数等于周期长度，即k＝4，由于移动项数是偶数，所以要做两次移动平均。
例如：2006年第一次移动平均的结果为：
T2006，2.5＝（y2006，1＋y2006，2＋y2006，3＋y2006，4）/4
T2006，3.5＝（y2006，2＋y2006，3＋y2006，4＋y2006，1）/4
……
则第二次移动平均的结果为：

……
即2006年第3季度的移动平均数为：

故2006年第3季度的季节比率为：
y2006，3/T2006，3＝2264.1/1627.9875＝1.3907
同理2006年第4季度的移动平均数为：

故2006年第4季度的季节比率为：
y2006，4/T2006，4＝1943.3/1833.0875＝1.0601
同理可得其他月份的移动平均数，进而可得相应的季节比率，最后即可求得季节指数。计算出季节指数后，将各实际观察值分别处除以相应的季节指数，从而剔除季节变动，计算公式为：y/S＝（T×S×I）/S＝T×I。计算结果如表所示。

绘制季节变动图，如图所示，从图中可以看出旺季是第3季度，淡季是第1季度。

绘制剔除季节变动后销售额及其趋势图，如图所示。

由图可知，可以用一元线性模型来预测各季度的销售额，设趋势方程为：Yt＝b0＋b1t，由Excel可得：b0＝2043.92，b1＝163.7064。所以剔除季节变动后销售额的趋势方程为：Yt＝2043.92＋163.7064t