初等模型练习题
一、初等模型
- 1.1 牙膏包装
-
- 1.1.1题目描述
- 1.1.2 问题分析
- 1.1.3 问题建设
- 1.1.4 模型
- 1.2 鲈鱼质量
-
- 1.2.1 题目描述
- 1.2.2 问题分析
- 1.2.3 问题假设
- 1.2.4 模型
- 1.3 圆盘加工
-
- 1.3.1 问题描述
- 1.3.2 思路
- 1.4 动物尺寸
- 1.5 体重&心率
-
- 1.5.1 问题描述
- 1.5.2 符号说明
- 1.5.3 模型
1.1 牙膏包装
题目来源:《数学模型》(第五版)–姜启源、谢金星、叶俊
1.1.1题目描述
在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗?比如佳洁士牙膏120g装的每支10.80元,200g装的每支15.80元,二者单位质量的价格比是1.14:1。使用比例方法构造模型解释这个现象。
(1)分析商品价格 C C C与商品质量 w w w的关系。价格由生产成本、包装成本和其他成本等决定,这些成本中有的与质量 w w w成正比,有的与表面积成正比,还有与 w w w无关的因素。
(2)给出单位质量价格 c c c与 w w w的关系,画出它的简图,说明 w w w越大 c c c越小,但随着 w w w的增加 c c c减小的程度变小,解释其实际意义。
1.1.2 问题分析
(1)价格由生产成本、包装成本和其他成本等决定。一般情况下生产成本与商品质量 w w w成正比;商品质量 w w w与包装容积 v v v成正比;包装成本与包装表面积 s s s成正比,其他与 w w w无关的成本我们假设其为常数。
1.1.3 问题建设
- 与 w w w无关的成本我们假设其为常数,且大包装小包装的其他成本相同。
- 存在一个特征尺寸 r r r满足 r 2 ∝ s r^2\propto s r2∝s则有 r 3 ∝ v r^3\propto v r3∝v。
- 商品价格与商品成本成正比。
1.1.4 模型
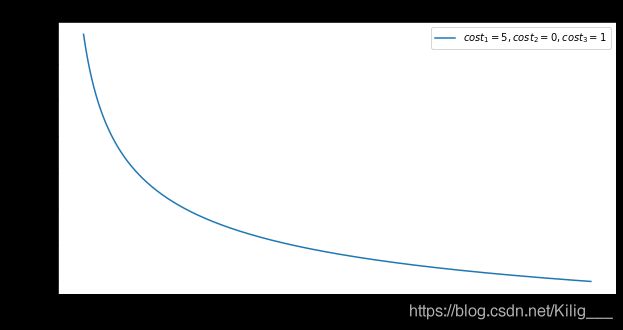
我们已知商品质量 w w w与包装容积 v v v成正比。由假设2我们可推出 s ∝ v 2 3 s\propto v^{\frac{2}{3}} s∝v32那么则有 s ∝ w 2 3 s\propto w^{\frac{2}{3}} s∝w32我们即可写出 s s s与 w w w的关系式 s = k 1 ∗ w 2 3 s = k_1*w^{\frac{2}{3}} s=k1∗w32,我们假设单位质量成本为 c o s t 1 cost_1 cost1;单位包装成本为 c o s t 2 cost_2 cost2;其余成本 c o s t 3 cost_3 cost3为恒定的常数。那么由假设3我们可有以下式子 C ∝ ( c o s t 1 ∗ w + c o s t 2 ∗ s + c o s t 3 ) 且 s = k 1 ∗ w 2 3 C \propto (cost_1*w+cost_2*s+cost_3) 且s = k_1*w^{\frac{2}{3}} C∝(cost1∗w+cost2∗s+cost3)且s=k1∗w32 C = K ∗ ( c o s t 1 ∗ w + c o s t 2 ∗ k 1 ∗ w 2 3 + c o s t 3 ) C = K*(cost_1*w+cost_2* k_1*w^{\frac{2}{3}}+cost_3) C=K∗(cost1∗w+cost2∗k1∗w32+cost3)对上式进行简化( K = 1 , c o s t 2 ∗ k 1 取 为 c o s t 2 K=1,cost_2*k_1取为cost_2 K=1,cost2∗k1取为cost2)则上式变为 C = c o s t 1 ∗ w + c o s t 2 ∗ w 2 3 + c o s t 3 C = cost_1*w+cost_2*w^{\frac{2}{3}}+cost_3 C=cost1∗w+cost2∗w32+cost3那么则有单位质量的售价 c = C w = c o s t 1 + c o s t 2 ∗ w − 1 3 + c o s t 3 ∗ w − 1 c = \frac{C}{w}=cost_1+cost_2*w^{-\frac{1}{3}}+cost_3*w^{-1} c=wC=cost1+cost2∗w−31+cost3∗w−1我们对其可视化如下图:
import numpy as np
import matplotlib.pylab as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 步骤一(替换sans-serif字体)
plt.rcParams['axes.unicode_minus'] = False # 步骤二(解决坐标轴负数的负号显示问题)
w = np.array([i for i in range(100,2500)])
cost_1 = 10
cost_2 = 1
cost_3 = 3
C = cost_1+cost_2*(w**(-1/3))+cost_3*(w**(-1.0))
plt.figure(figsize=(10,5));
plt.title("单位质量的售价随质量的变化")
plt.xlabel("$w$")
plt.ylabel("$c$")
plt.plot(w,C,'-',label="$cost_1 = 5,cost_2 = 0,cost_3 = 1$")
plt.legend()
plt.show()
我们从图中可以看出,单位质量的售价会随着质量的增加而变少。但是单位售价的减少值也会随着质量的增加而变少(曲线逐渐趋于平缓)因此不要过于贪图大包装的商品。
1.2 鲈鱼质量
1.2.1 题目描述
一垂钓俱乐部鼓励垂钓者将钓上的鱼放生,打算按照放生的鱼的质量给予奖励,俱乐部只准备了一把软尺进行测量,请你设计按照测量长度估计鱼的质量的方法。假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长)

1.2.2 问题分析
由于都是鲈鱼,我们可以假设其平均密度都是一样的,那么鱼的质量与其体积成正比。根据所给出身长与胸围建立模型求得鱼的体积即可。
1.2.3 问题假设
- 各条鲈鱼的平均密度都一样
- 各条鲈鱼的基本形状无过大差别
1.2.4 模型
我们假设鲈鱼存在一个特征半径 r r r满足鲈鱼的胸围 l = 2 π r l = 2\pi r l=2πr那么则有鲈鱼特征截面积 s = π r 2 s = \pi r^2 s=πr2即可推导出鲈鱼的体积 v = s ∗ h = π r 2 ∗ h v = s*h = \pi r^2*h v=s∗h=πr2∗h, h h h为鲈鱼的身长。而鱼的体重 m = ρ v m = \rho v m=ρv我们即可假定一个参数 k 1 = ρ π k_1=\rho \pi k1=ρπ满足 m = k 1 r 2 h m = k_1r^2h m=k1r2h.
我们也可以假设鱼的体积 v ∝ h 3 v \propto h^3 v∝h3得到 m = k 2 h 3 m = k_2h^3 m=k2h3根据已给数据最小二乘拟合得到 k 1 = 0.03224772 , k 2 = 0.01459115 k_1=0.03224772,k_2=0.01459115 k1=0.03224772,k2=0.01459115
import numpy as np
import matplotlib.pylab as plt
h = np.array([36.8,31.8,43.8,36.8,32.1,45.1,35.9,32.1])
l = np.array([24.8,21.3,27.9,24.8,21.6,31.8,22.9,21.6])
m = np.array([765,482,1162,737,482,1389,652,454])
def Pfun1(t,k1):#第一个函数的拟合
return k1*(t[0]**2)*t[1]
def Pfun2(t,k2):#第二个函数的拟合
return k2*(t[1]**3)
lh = np.vstack((l, h))
popt1, pcov1=curve_fit(Pfun1, lh, m)
popt2, pcov2=curve_fit(Pfun2, lh, m)
print("k1的拟合值为:", popt1)
print("k2的拟合值为:", popt2)
'''
输出结果:
k1的拟合值为: [0.03224772]
k2的拟合值为: [0.01459115]
'''
1.3 圆盘加工
1.3.1 问题描述
用已知尺寸的矩形板材加工半径一定的圆盘,给出几种简便、有效的排列方法,使加工出尽可能多的圆盘
1.3.2 思路
用正方形、六边形代替圆盘
1.4 动物尺寸
动物园里的成年热血动物靠饲养的食物维持体温基本不变,在一些合理、简化的假设下建立动物的饲养量与动物的某个尺寸的关系。
假设动物的特征尺寸为 l l l满足表面积 S ∝ l 2 S\propto l^2 S∝l2。由于体温基本不变,且动物体内的热量主要由表面散失。所以可以有进食量 w ∝ S ∝ l 2 w\propto S \propto l^2 w∝S∝l2
1.5 体重&心率
1.5.1 问题描述
生物学家认为,对于休息状态的热血动物,消耗的能量主要用于维持体温,能量与从心脏到全身的血流量成正比,而体温主要通过身体表面散失,建立一个动物体重(单位:g)与心率(单位:次/min)之间关系的模型,并用下面的数据加以检验。

1.5.2 符号说明
| 符号 | 意义 |
|---|---|
| Q Q Q | 热量 |
| q q q | 每次泵出的血流量 |
| v v v | 心率 |
| S S S | 动物表面积 |
| m m m | 动物质量 |
| l l l | 动物特征尺寸 |
| V V V | 动物体积 |
1.5.3 模型
热量 Q Q Q与动物表面积 S S S成正比,我们可以知道 l 2 ∝ S , l 3 ∝ V l^2\propto S,l^3\propto V l2∝S,l3∝V因此有 S ∝ V 2 3 S \propto V^{\frac{2}{3}} S∝V32而 V V V与动物质量 m m m成正比。通过常识我们可以知道 q ∝ m q\propto m q∝m而 Q = q v Q = qv Q=qv
由上述描述我们可以建立式子
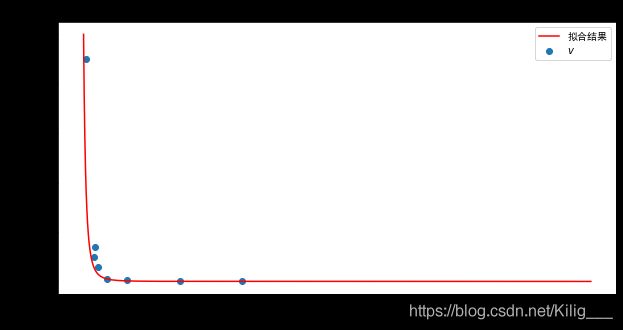
Q = k 1 m 2 3 = k 2 m v Q = k_1m^{\frac{2}{3}} = k_2mv Q=k1m32=k2mv k 1 , k 2 k_1,k_2 k1,k2均为常数。化简我们可以得到 v = k m − 1 3 v = km^{-\frac{1}{3}} v=km−31利用最小二乘拟合得到 k = 2089.73532836 k =2089.73532836 k=2089.73532836
import numpy as np
import matplotlib.pylab as plt
from scipy.optimize import curve_fit
plt.rcParams['font.sans-serif'] = ['SimHei'] # 步骤一(替换sans-serif字体)
plt.rcParams['axes.unicode_minus'] = False # 步骤二(解决坐标轴负数的负号显示问题)
m = np.array([25,200,2000,5000,30000,50000,70000,450000])
v = np.array([670,420,205,120,85,70,72,38])
def Pfun1(t,k):#第一个函数的拟合
return k*(t**(-1/3))
popt1, pcov1=curve_fit(Pfun1, m,v)
print("k的拟合值为:", popt1)
def P(m):
return 2089.73532836*(m**(-1/3))
x = np.array([i for i in range(500000)])
y = P(x)
plt.figure(figsize=(10,5));
plt.title("m随v的变化")
plt.xlabel("$m$")
plt.ylabel("$v$")
plt.scatter(v,m,label="$v$")
plt.plot(y,x,'r',label = "拟合结果")
plt.legend()
plt.show()
'''
k的拟合值为: [2089.73532836]
'''