机器学习常见评价指标
机器学习常见评价指标
0 引言
\qquad 在建模的时候,不论是一般机器学习还是深度学习,都要有评价指标进行模型效果的衡量,评价指标是对于一个模型效果的数值型量化。一般来说,评价指标分为分类问题和回归问题,下面就分别介绍两类问题的评价指标。
1 分类问题常见评价指标
1.1 基础知识
分类问题中,又可以分为二分类和多分类问题:
- 二分类问题:accuracy、precision、recall、F1-score、AUC、ROC曲线
- 多分类问题:accuracy、宏平均、微平均、F1-score
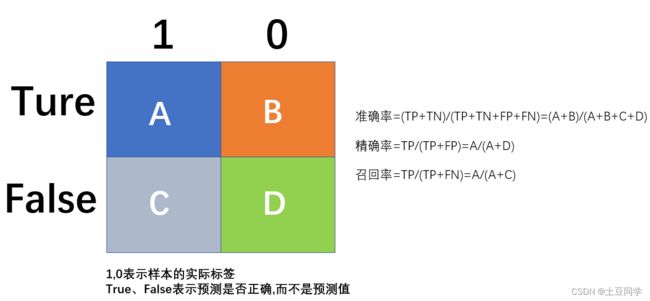
在介绍各评价指标的计算方法之前,还要介绍一下TP(True Positive, 真阳性)、TN(True Negative, 真阴性)、FP(False Positive, 假阳性)、FN(False Negative, 假阴性)
 TP 表示将实际标签为正的样本判断为正的样本数量或者比例;
TP 表示将实际标签为正的样本判断为正的样本数量或者比例;
FP 表示将实际标签为负的样本判断为正的样本数量或者比例;
FN 表示将实际标签为正的样本判断为负的样本数量或者比例;
TN 表示将实际标签为负的样本判断为负的样本数量或者比例。
有时候很容易记混,所以我自己有个记忆方法:第一个字母代表是否判断正确,第二个字母代表样本的预测值。
1.2 各指标计算方法
现在网上很多人把precision和accuracy、精确率和准确率混为一谈,这是不对的,如图所示:
1.2.1 准确率(Accuracy)
准确率(Accuracy)表示所有的预测样本中,预测正确的比例,计算方法如下:
A c c u r a c y ( 准 确 率 ) = T P + T N T P + F P + F N + T N Accuracy(准确率)={TP+TN\over{TP+FP+FN+TN}} Accuracy(准确率)=TP+FP+FN+TNTP+TN
1.2.2 精确率(Precision)
精确率(Precision)表示预测为正样本的样本中,实际为正样本的比例。精确率考虑的是正样本被预测正确的比例。计算方法如下:
P r e c i s i o n ( 精 确 率 ) = T P T P + F P Precision(精确率)={TP\over{TP+FP}} Precision(精确率)=TP+FPTP
1.2.3 召回率(Recall)
召回率(Recall)表示实际为正样本的样本中,预测为正样本的比例。召回率考虑的是正样本的召回的比例。计算方法如下:
R e c a l l ( 召 回 率 ) = T P T P + F N Recall(召回率)={TP\over{TP+FN}} Recall(召回率)=TP+FNTP
1.2.4 F1-socre
其实精确率和召回率之间是存在矛盾的,很多场景下,模型最终结果往往实在精确率和召回率之间找到平衡点。F1-socre是兼顾精确率和召回率的参数,之所以使用调和平均而不是算术平均,是因为在算术平均中,任何一方对数值增长的贡献相当,任何一方对数值下降的责任也相当;而调和平均在增长的时候会偏袒较小值,也会惩罚精确率和召回率相差巨大的极端情况,很好地兼顾了精确率和召回率。F1-socre计算方法如下:
F 1 = 2 ∗ P r e c i s i o n ∗ R e c a l l P r e c i s i o n + R e c a l l F1={2*Precision*Recall\over{Precision+Recall}} F1=Precision+Recall2∗Precision∗Recall
1.2.5 AUC值以及ROC 曲线
AUC(Area Under ROC Curve)值为ROC 曲线下面积,表示模型或预测结果的可靠性,越接近1,可靠性越高。
1.2.6 Macro avg(宏平均)
Macro avg(宏平均)在为每一指标计算时,会对每一类别赋予相同的权重,即每个类别的指标的算术平均值。可能理解起来比较抽象,看以下例子:
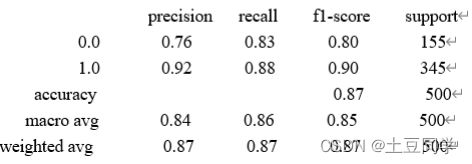
比如macro avg of precision = p r e c i s i o n ( C = 0 ) + p r e c i s i o n ( C = 1 ) 2 = ( 0.76 + 0.92 ) 2 = 0.84 = {precision(C=0)+precision(C=1) \over 2} = {(0.76+0.92) \over 2}=0.84 =2precision(C=0)+precision(C=1)=2(0.76+0.92)=0.84
1.2.7 Micro avg(微平均)
Micro avg(微平均)为所有类别的准确率,即所有预测正确的样本数量的比例:
M i c r o − a v g = ( T P + T N ) / ( T P + F P + T N + F N ) Micro-avg =(TP + TN) / (TP + FP + TN + FN) Micro−avg=(TP+TN)/(TP+FP+TN+FN)
TP实际标签为正的样本判断为正的样本数量;TN 表示将实际标签为负的样本判断为负的样本数量
TP + FP + TN + FN表示所有样本数量
上图中并没有micro-avg,但并不妨碍我们计算:
预测对的正样本TP=345*0.88
预测对的负样本TN=155*0.83
m i c r o − a v g = 345 ∗ 0.88 + 155 ∗ 0.83 ( 155 + 345 ) = 0.8645 micro-avg={345 * 0.88+155 * 0.83 \over (155+345) }= 0.8645 micro−avg=(155+345)345∗0.88+155∗0.83=0.8645
1.2.8 weighted-avg(权重平均)
weighted-avg(权重平均)是因为宏平均在计算的时候,每个类别赋予的权重相同,但如果存在样本不平衡的情况,那这种方法就不太公平,所以权重平均便根据每个类别的样本数量,赋予不同的权重。权重平均其实就是所有类别的f1加权平均,主要针对F1值,计算方式如下:
w e i g h t e d a v g = 负 样 本 比 例 ∗ 负 样 本 F 1 + 正 样 本 比 例 ∗ 正 样 本 F 1 = 0.8 ∗ 155 / 500 + 0.9 ∗ 345 / 500 = 0.869 = 0.87 weighted avg = 负样本比例 * 负样本F1 + 正样本比例 * 正样本F1 = 0.8 * 155 / 500 + 0.9 * 345 / 500 = 0.869=0.87 weightedavg=负样本比例∗负样本F1+正样本比例∗正样本F1=0.8∗155/500+0.9∗345/500=0.869=0.87
2 回归(预测)问题常见评价指标
回归或预测问题常见评价指标如下:平均绝对误差(Mean Absolute Error,MAE),均方误差(Mean Squared Error,MSE),均方根误差(Root Mean Square Error, RMSE),均方根误差(Root Mean Squared Error) , R2(R-Square).
2.1 平均绝对误差(Mean Absolute Error,MAE)
平均绝对误差(Mean Absolute Error,MAE)是预测值与真实值之差的绝对值,反映了预测值与真实值误差的实际情况,计算公式为 M A E = 1 N ∑ i = 1 N ∣ y i − y i ^ ∣ MAE={1 \over N} \sum_{i=1}^N|y_i-\hat{y_i}| MAE=N1i=1∑N∣yi−yi^∣
MAE的计算在sklearn中调用代码为:
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(y_true, y_pred) # y_true为真实值,y_pred为预测值
2.2 均方误差(Mean Squared Error, MSE)
均方误差(Mean Squared Error, MSE)是预测值与真实值之差平方的期望值。MSE的值越小,说明预测模型描述实验数据具有越好的精确度。计算公式为 M S E = 1 N ∑ i = 1 N ( y i − y i ^ ) 2 MSE={1 \over N}\sum_{i=1}^N(y_i-\hat{y_i})^2 MSE=N1i=1∑N(yi−yi^)2
MSE的计算在sklearn中调用代码为:
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_true, y_pred) # y_true为真实值,y_pred为预测值
2.3 均方根误差(Root Mean Square Error, RMSE)
均方根误差(Root Mean Square Error, RMSE)是MSE的平方根,为预测值和真实值差异的样本标准差。均⽅根误差为了说明样本的离散程度,拟合时,RMSE越小越好。均方根误差与标准差的研究对象不同,均方根误差用来衡量预测值与真实值之间的偏差,而标准差用于衡量一组数据的离散程度。计算公式为
R M S E = M S E = S S E N = 1 N ∑ i = 1 N ( y i − y i ^ ) 2 RMSE=\sqrt{MSE}=\sqrt{SSE\over N}=\sqrt{{1 \over N}\sum_{i=1}^N(y_i-\hat{y_i})^2} RMSE=MSE=NSSE=N1i=1∑N(yi−yi^)2
其中,SSE(error sum of squares)为残差平方和,具体可见以下博文:
数学建模方法—【03】拟合优度的计算(python计算)
RMSE的计算在sklearn中调用代码为:
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_true, y_pred) # y_true为真实值,y_pred为预测值
rmse = Sqrt(mse)
2.4 R平方值(R-Squared)
R平方值(R-Squared)又称拟合优度,反映了回归模型对数据的拟合程度,取值范围为(0,1], R 2 R^2 R2越接近1,表明用x的变化来解释y值变化的部分就越多,回归的拟合程度就越好。拟合优度的具体计算过程同样见这篇文章:
数学建模方法—【03】拟合优度的计算(python计算)
当然,sklearn中也可以直接调用:
from sklearn.metrics import r2_score
r2 = r2_score(y_true, y_pred) # y_true为真实值,y_pred为预测值
参考:
https://blog.csdn.net/weixin_43922901/article/details/106097774
https://www.jianshu.com/p/9e0caf109e88
https://blog.csdn.net/Bruce_0712/article/details/117778741
https://blog.csdn.net/qq_43403025/article/details/108285275
ps://www.jianshu.com/p/9e0caf109e88
https://blog.csdn.net/Bruce_0712/article/details/117778741
https://blog.csdn.net/qq_43403025/article/details/108285275
https://blog.csdn.net/fanfangyu/article/details/122929133