控制器设计中的传感数据滤波——IIR滤波器的Matlab辅助设计

实际的控制中，传感器的数据总是带有噪声，直接使用容易导致控制器的震荡。
因此，对传感器数据进行滤波是需要特别考虑的。
由于控制器通常由计算机运算，因此无论是传感信号还是控制信号都是数字信号，所以需要设计数字滤波器。
FIR和IIR是两种常用的数字滤波器实现方法，这篇博客将会介绍如何设计一个经典的IIR数字滤波器。

1 IIR滤波器

IIR滤波器的形式为（离散域形式）：
$$H(z)=\frac{Y(z)}{X(z)}=\frac{{\sum }_{p=0}^M{a}_p{z}^{-p}}{{\sum }_{p=0}^N{b}_p{z}^{-p}}$$
通常，$b_0=1$。$x$代表输入，$y$代表输出。
改写成差分方程形式就是：
$$y(k)+b_{1}y(k-1)+b_{2}y(k-2)+...=a_{0}x(k)+a_{1}x(k-1)+a_{2}x(k-2)+...$$
即：
$$y(k)=-\sum _{p=1}^N{b}_{p}y(k-p)+\sum _{p=0}^M{a}_{p}x(k-p)$$
这里可以看到，IIR滤波器是既和输入有关，也和输出有关的，也就是说这个滤波器是具有反馈的。
与之相对应的FIR滤波器的形式如下：
$$H(z)=\frac{Y(z)}{X(z)}=\sum _{n=0}^{N-1}h(n)z^{-n}$$
即：
$$y(k)=\sum _{n=0}^{N-1}h(n)x(k-n)$$
即FIR是单纯和输入有关的，没有反馈。

2 滤波器设计

实际上，数字滤波器的结构非常简单，代码实现上也非常容易。
数字滤波器的核心在于如何确定滤波器中的各项系数，这是滤波器设计的重中之中。我们学习的庞大复杂的数字滤波器的相关理论也是为其服务的。
所幸，如今要设计滤波器，使用MATLAB就可以了，不需要自己去进行复杂的计算。

一般来说，IIR滤波器的设计可以分为四个步骤：

1. 选择一种模拟滤波器（这里通常可以是巴特沃斯、切比雪夫滤波器等）
2. 确定数字滤波器的截止频率（数字滤波器和模拟滤波器截止频率存在对应关系）
3. 计算模拟滤波器截止频率，并计算模拟滤波器中各个参数的值
4. 利用双线性变换，将模拟滤波器中的s用z代替，得到最终的数字滤波器

如今，我们拥有了MATLAB的工具，设计一个IIR滤波器只需要一句代码就可以了。
选取一阶低通巴特沃斯滤波器为例，其IIR数字滤波器的系数可由下面的语句计算：

[a,b]=butter(1, 0.1,'low');
% 其中：
% butter代表巴特沃斯滤波器
% 1代表1阶
% 0.1代表数字滤波器的截止频率占采样频率的比值，例如传感器采样频率是100hz，期望截止频率是10hz，那么这个比值就是：10hz/100hz=0.1
% 'low'代表低通滤波器
% a和b代表滤波器系数

当然，想要选择哪种模拟滤波器进行IIR的实现，大家可以自由选择，MATLAB中都有对应工具。

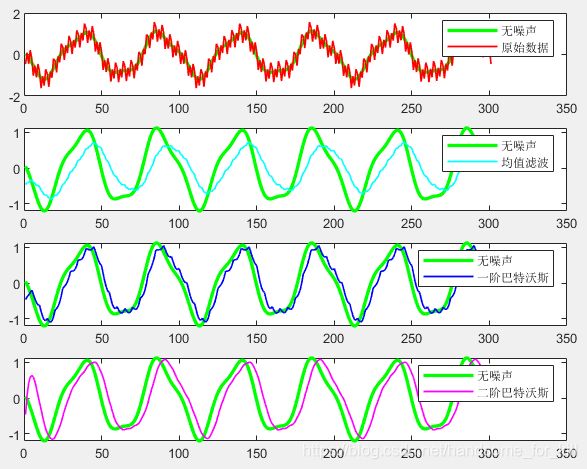
3 MATLAB示例

为了更好的说明，如何利用MATLAB实现数字滤波，我写了一个程序：

clc;
clear all;
close all;
% 生成有噪声数据
dt = 0.01; % 采样频率: 100hz
f1 = 2;  % 频率成分1
f2 = 5;  % 频率成分2
f3 = 20; % 频率成分3
f4 = 40; % 频率成分4
X = [];
G = [];
for t = 0:dt:3
    g = -sin(f1*2*pi*t+0.1) + 0.2*sin(f2*2*pi*t+0.8);
    x = g - 0.3*sin(f3*2*pi*t+0.8) + 0.4*sin(f4*2*pi*t-0.8);
    G = [G;g];
    X = [X;x]; 
end
% 展示结果
% 原始数据
subplot(4,1,1)
plot(G, 'g-', 'LineWidth', 2)
hold on
plot(X,'r-', 'LineWidth', 1)
hold on
legend('无噪声', '原始数据')
% 低通滤波
sX0 = X;
alpha = 0.1;
for ii=2:length(X)
    sX0(ii) = (1-alpha)*sX0(ii-1) + alpha*X(ii);
end
subplot(4,1,2)
plot(G, 'g-', 'LineWidth', 2)
hold on
plot(sX0,'c-', 'LineWidth', 1)
hold on
legend('无噪声', '一阶低通滤波')
% IIR     
% b0*Y(k)-b1*Y(k-1)-b2*Y(k-2)-...=a0*X(k)+a1*X(k-1)+a2*X(k-2)+...
% Y(k)=(b1*Y(k-1)+b2*Y(k-2)+...+a0*X(k)+a1*X(k-1)+a2*X(k-2)+...)/b0
% 一阶巴特沃斯滤波器
[a,b]=butter(1,0.1,'low'); % 10hz/100hz=0.1
sX1 = butterworth_filter(X, a, b, 1);
subplot(4,1,3)
plot(G, 'g-', 'LineWidth', 2)
hold on
plot(sX1,'b-', 'LineWidth', 1)
hold on
legend('无噪声', '一阶巴特沃斯')
% 二阶巴特沃斯滤波器
[a,b]=butter(2,0.1,'low'); % 10hz/100hz=0.1
sX2 = butterworth_filter(X, a, b, 2);
subplot(4,1,4)
plot(G, 'g-', 'LineWidth', 2)
hold on
plot(sX2,'m-', 'LineWidth', 1)
hold on
legend('无噪声', '二阶巴特沃斯')
function smooth_data = butterworth_filter(data, a, b, order)
    smooth_data = data;
    for ii = order+1:length(data)
        parta = 0;
        for jj = 1:order+1
        	parta = parta + a(jj)*data(ii-jj+1);
        end
        partb = 0;
        for kk = 2:order+1
        	partb = partb - b(kk)*smooth_data(ii-kk+1);
        end
        smooth_data(ii) = parta + partb;
    end
end

运行结果如下：

4 参考资料

• 如何快速设计一个IIR滤波器