机器学习（4）——无监督学习

目录

1无监督学习

1.1 k-均值聚类算法

1.2 新型传染病聚类分析

1.3 机器学习模型保存

1.4 高斯混合模型

1.5 层次聚类

2 分类模型泛化

2.1 数据划分有效性

2.2 更有效数据划分

2.2.1 交叉验证分离器

2.2.2 打乱交叉验证

2.3 模型参数优化

2.3.1 网络搜索

2.3.2 交叉验证网络搜索

2.3.3 管道使用

2.4 主成分分析

2.5 流形学习

---

1无监督学习

1.1 k-均值聚类算法

无监督学习是指事先并不知道实际的输出和分类结果，要做的就是从一堆数据中心尝试找到新的知识。最基本的算法有k-均值聚类算法（k-means clustering algorithm）。k-均值聚类思路是将每个数据点分配给最近的簇中心，然后将每个簇中心设置为所分配的所有数据点的平均值，当簇的分配不再变化时，算法则结束。

k-均值聚类算法具体可以描述如下：

（1）任意选择k个点，作为初始的聚类中心。

（2）遍历每个对象，分别对每个对象求与k个中心点的距离，把对象划分到与最近的中心所代表的类别中去。

（3）对于每一个中心点，遍历他们所包含的对象，计算这些对象所有维度的和的中值，获得新的中心点。

（4）计算当前状态下的损失，如果当前损失比上一次迭代的损失相差大于某一值（如1），则继续执行第（2）、（3）步，直到连续两次的损失差为某一设定值为止（达到最优，通常设置为1）。

聚类是将数据划分为组，这些组称为簇。聚类的目的就是从数据中发现可能的新的规律。

单相接地故障k-均值聚类算法实例：

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
from sklearn.cluster import KMeans
df1 = pd.read_csv('E:\PYTHON\ground_feature0.csv') #读取特征向量
data = df1.values
X = data[:,0:2] #构建要分割的数据,前两列
y = data[:,2] #构建分类目标
#分割数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=10)
def plot_decision_regions(X,y,classifier,test_idx=None,resolution=0.02):#两类分类曲线绘图函数定义
    #setup marker generator and color map
    markers = ('s','x','o','^','v')
    colors = ('red','blue','lightgreen','gray','cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    #plot the decision surface
    x1_min,x1_max = X[:,0].min()-1,X[:,0].max()+1
    x2_min,x2_max = X[:,1].min()-1,X[:,1].max()+1
    xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),np.arange(x2_min,x2_max,resolution))
    Z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1,xx2,Z,alpha=0.4,cmap=cmap)
    plt.xlim(xx1.min(),xx1.max())
    plt.ylim(xx2.min(),xx2.max())
    #plot all sample
    X_test,y_test = X[test_idx,:],y[test_idx]
    for idx,cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y==cl,0],y=X[y==cl,1],alpha=0.8,c=cmap(idx),marker=markers[idx],label=cl)
gf_kmeans = KMeans(n_clusters=2)
gf_kmeans.fit(X_train)
plot_decision_regions(X,y,classifier=gf_kmeans,test_idx=range(16,22))
plt.xlabel("Drop percentage KMeans")
plt.ylabel("Ascending mutation value")
plt.legend(loc='upper right')
plt.title('One-phase ground')
plt.show()
gf_new = np.array([[0.590,1.9]])
print('KMeans Training set scores: {:.2f}'.format(gf_kmeans.score(X_train, y_train)))
print('KMeans Test set scores: {:.2f}'.format(gf_kmeans.score(X_test, y_test)))
print('KMeans New array Prediction: {}'.format(gf_kmeans.predict(gf_new)))

运行结果如下：

KMeans Training set scores: -68.07
KMeans Test set scores: -14.40
KMeans New array Prediction: [1]

k-均值聚类分类曲线

这种聚类分类曲线，在解决单相接地故障分类上效果并不好。

1.2 新型传染病聚类分析

判断一种新型病是否能构成新的传染病类型，其实可以根据医学经验构建出该病前期阶段病例特征向量，一种可能的特征向量构造如下：

[同一地方，体温，肺CT，三天治疗效果，七天治疗效果，14天增加人数比例，病理相似性，异常级别]

该向量由8个分量组成，各自的含义如下：

同一地方：表示病人是否到过同一区域。1~0的数据，1到过核心地带，0没有。中间数据表示接近核心地带的边缘强度，如0.7表示病人接近核心地带的边缘。

体温：表示人的体温是否正常。1~0的数据，1代表高烧，0代表正常。中间数据表示低烧。

肺CT：表示病人肺部病理类似度。1~0的数据，1代表完全相似，0代表不相似。中间数据表示相似大小。

三天治疗效果：1~0的数据，1代表恶化，0代表治愈。中间数据代表病情的轻重分级。

七天治疗效果：1~0的数据，1代表恶化，0代表治愈。中间数据代表病情的轻重分级。

14天增加人数比例：按净增加人数除以总人数计算，总人数为历史人数+净增人数，将此数据限制在1~0。

病理相似性：1~0的数据，表示病理之间是否有相似性，1代表完全相似，0代表不相似。中间数据表示相似程度。

异常级别：表示医生认为此病比传统疾病异常与否。1~0的数据，1代表异常最大，0代表不异常。中间数据代表异常强度。

模拟数据desease_1.csv文件：

desease_1.csv文件获取：

链接：https://pan.baidu.com/s/1rtNYuTNjmZjmEWK5fTczdw 
提取码：whj6

下面对一种传染病前期病情k-均值聚类分析，机器识别程序如下：

import pandas as pd
from sklearn.cluster import KMeans
da = pd.read_csv('E:\PYTHON\desease_1.csv')
data1 = da.values
estimator = KMeans(n_clusters=2) #n_clusters为簇的个数，分类数目
estimator.fit(data1)
label_pred = estimator.labels_
print(label_pred)

运行结果如下：

[1 0 1 1 0 1 1 0 0]

由运行结果可以看出，通过两类聚类划分，第一、三、四、六、七条数据划分为了一类，说明这些数据有共同特点，具有新型传染病共同特征。

1.3 机器学习模型保存

分类模型参数保存后，下次使用时调用即可。保存Python分类模型需要用到joblib包。

例如，将上述分类模型保存到desease_cluster.pkl文件中。

import pandas as pd
from sklearn.cluster import KMeans
import joblib
da = pd.read_csv('E:\PYTHON\desease_1.csv')
data1 = da.values
estimator = KMeans(n_clusters=2) #n_clusters为簇的个数，分类数目
estimator.fit(data1)
label_pred = estimator.labels_
#print(label_pred)
joblib.dump(estimator,'desease_cluster.pkl') #将estimator模型保存到desease_cluster.pkl中
des = joblib.load('desease_cluster.pkl') #读取模型分类数据
print(des.labels_) #显示分类目标

运行结果如下：

[0 1 0 0 1 0 0 1 1]

当通过聚类分析构建出新的分类模型后，就可以对新病例分类预测。

import pandas as pd
from sklearn.cluster import KMeans
import joblib
da = pd.read_csv('E:\PYTHON\desease_1.csv')
data1 = da.values
estimator = KMeans(n_clusters=2) #n_clusters为簇的个数，分类数目
estimator.fit(data1)
label_pred = estimator.labels_
#print(label_pred)
joblib.dump(estimator,'desease_cluster.pkl') #将estimator模型保存到desease_cluster.pkl中
des = joblib.load('desease_cluster.pkl') #读取模型分类数据
#print(des.labels_) #显示分类目标

x = [1,1,1,1,1,1,1,1] #新病例向量
zz = [x]
print(des.predict(zz)) #新病例预测归类

运行结果如下：

[0]

由运行结果可知，使用dump()函数将分类模型保存在当前目录下的desease_cluster.pkl文件中。使用load()函数将模型参数读出赋值给des，通过类标和预测函数就可以进行相关操作和新向量的识别，这样就不需要重新训练分类器了。

1.4 高斯混合模型

概率论中高斯分布的概率密度函数定义如下：

其中，参数为均值；为标准差，决定分布的幅度。而高斯混合模型（Gaussian Mixture Model, GMM）就是将多个高斯分布进行混合来刻画数据的分布。其公式如下：

其中，K表示有K个高斯分布；和对应第i个高斯分布的参数；为混合系数，且必须为正数，用来表示权重，所有的混合系数之和必须为1。

当使用GMM进行模型训练时，最常用的方法就是期望最大算法（Expectation-Maximization algorithm, EM）。其基本思想是通过模型来计算数据的期望值，并不断更新各个参数使得期望值最大化，通过迭代的方式直到两次迭代中参数变化十分微小为止。GMM的训练过程与k-均值聚类算法有着很大的相似之处。k-均值聚类算法是不断计算与各个簇中心的距离，并选择最小距离作为自己的类，而GMM是不断迭代与每部分之间的概率并选择最大概率作为自己的类。

下面我们利用鸢尾花数据集进行GMM训练：

from sklearn.datasets import load_iris
from sklearn.mixture import GaussianMixture
import numpy as np
#加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target
#构建高斯混合模型
gmm = GaussianMixture(n_components=3)
gmm.fit(X)
#分类结果
label_pred = gmm.predict(X)
#GMM分类结果与原始分类结果比较
print('GMM分类结果:\n{}'.format(label_pred))
print('原始分类结果:\n{}'.format(y))
print('GMM set score:{}'.format(np.mean(y==label_pred)))

运行结果如下：

GMM分类结果:
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 0 2 0
 0 0 0 2 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
原始分类结果:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
GMM set score:0.3333333333333333
#注意：运行次数不同最后结果不同，可多次运行比较结果

最后得分情况不理想。但进一步观察输出的分类标签可以发现，GMM分类结果中标签为“1”的类与原始分类标签为“0”的类的个数相同，GMM分类结果中标签为“0”的类与原始分类标签为“1”的类的个数相同，从标签相对数量上来看，GMM训练后的分类效果是十分理想的。由于对标签的设置无法和原始数据完全相同，从而造成了这种表面上的不理想效果。其实可以修改代码，将GMM分类结果的标签类别表示含义修改为和原始标签相同，再看得分情况。

将GMM分类结果的标签类别表示含义修改为和原始标签相同后的改进程序：

from sklearn.datasets import load_iris
from sklearn.mixture import GaussianMixture
import numpy as np
#加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target
#构建高斯混合模型
gmm = GaussianMixture(n_components=3)
gmm.fit(X)
#分类结果
label_pred = gmm.predict(X)

#定义欧氏距离函数
def distances(a,b):
    dist = np.sqrt(np.sum(np.square(a-b)))
    return dist
#原始均值矩阵
mean = np.array([np.mean(X[y==i],axis=0) for i in range(3)])
#GMM均值矩阵
gmm_mean = gmm.means_
#调整标签以适应数据集中的标签
label_pred_new = np.zeros(len(y))
for change in range(3):
    dist_min = 100
    for j in range(3):
        #求均值矩阵gmm_mean第i行与均值矩阵mean的每一行的距离
        dist = distances(np.array(gmm_mean[change]),np.array(mean[j]))
        #找到距离最小的一行进行标记
        if dist

运行结果如下：

GMM分类结果:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 2 1
 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
原始分类结果:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
GMM set score:0.9666666666666667
#注意：运行次数不同最后结果不同，可多次运行比较结果

由运行结果可以发现，使用GMM进行分类后的结果基本与原分类结果相同。

1.5 层次聚类

层次聚类也是聚类算法中的一种，层次聚类分为“自上而下”和“自下而上”两种聚类方法。“合成聚类算法”就是一种“自下而上”的聚类算法，该算法的基本思路如下：

（1）将每个对象都看成一个聚类；

（2）计算每个聚类之间的距离，找出距离最小的两个聚类将其归为一类；

（3）重复步骤（2），直到将所有聚类归为一类，生成一棵有层次的聚类树。同时需设置类别个数作为迭代终止条件。

利用层次聚类对鸢尾花数据集进行聚类分析：

from sklearn.datasets import load_iris
from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt

#加载鸢尾花数据集
iris = load_iris()
X = iris.data

#使用合成聚类算法进行分类
iris_ac = AgglomerativeClustering(n_clusters=3)
iris_ac.fit(X)

#将分类结果可视化
plt.scatter(X[:,0],X[:,1],c=iris_ac.labels_)
plt.title('AHC Training Result')
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.show()

运行结果如下：

由运行结果可以发现，该算法在分类上具有较高的可靠性，基本上把3种鸢尾花做出了正确的分类。

2 分类模型泛化

2.1 数据划分有效性

Python语言编写有监督学习算法的思路：

（1）构建训练数据集，数据集可以保存CSV文件格式；

（2）使用train_test_split()分割数据集，将数据划分为训练数据集和测试数据集两部分；

（3）利用fit()函数在训练数据集上构建模型；

（4）利用score()函数在测试数据集上评判分类模型好坏。

使用train_test_split()函数单次分割数据集，有一个潜在的问题存在，就是某一次分割的数据结果可能对训练模型有利，也可能不利。为了提高数据使用的效率，可以使用交叉验证方式。这种方法比单次划分训练数据集和测试数据集方法更加全面有效。

交叉验证思路是将数据多次划分，并训练多个模型。例如，5折交叉验证思路是将数据大致分为5个部分，将1/5数据用于测试，4/5数据用于训练，构建出一个分类模型。然后根据组合的思路，再将另外一组的1/5数据用于测试，4/5数据用于训练，构建出另一个分类模型。如此反复，构建出5个分类模型。通过使用交叉验证技术，可以最大化利用数据和提高模型的泛化能力。

对比一下单次划分数据的决策树模型分类与5折交叉验证所训练模型的得分差异。

首先，决策树模型分类程序如下：

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
from sklearn.tree import DecisionTreeClassifier
df1 = pd.read_csv('E:\PYTHON\ground_feature0.csv') #读取特征向量
data = df1.values
X = data[:,0:2] #构建要分割的数据,前两列
y = data[:,2] #构建分类目标
#分割数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=10)
gf_tree = DecisionTreeClassifier(criterion='entropy',max_depth=3,random_state=0)
gf_tree.fit(X_train,y_train)
print('Tree Training set scores: {:.2f}'.format(gf_tree.score(X_train, y_train)))
print('Tree Test set scores: {:.2f}'.format(gf_tree.score(X_test, y_test)))
gf_new =np.array([[0.490,1.1]]) #设置新特征向量
print('Tree New array Prediction: {}'.format(gf_tree.predict(gf_new)))

运行结果如下：

Tree Training set scores: 1.00
Tree Test set scores: 1.00
Tree New array Prediction: [0.]

其次，交叉验证程序如下:

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score
df1 = pd.read_csv('E:\PYTHON\ground_feature0.csv') #读取特征向量
data = df1.values
X = data[:,0:2] #构建要分割的数据,前两列
y = data[:,2] #构建分类目标
#分割数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=10)
gf_tree = DecisionTreeClassifier(criterion='entropy',max_depth=3,random_state=0)
gf_tree.fit(X_train,y_train)
# print('Tree Training set scores: {:.2f}'.format(gf_tree.score(X_train, y_train)))
# print('Tree Test set scores: {:.2f}'.format(gf_tree.score(X_test, y_test)))
# gf_new =np.array([[0.490,1.1]]) #设置新特征向量
# print('Tree New array Prediction: {}'.format(gf_tree.predict(gf_new)))
scores = cross_val_score(gf_tree,X_train,y_train,cv=5)
#scores = cross_val_score(gf_tree,X,y,cv=5)
print('Cross-validation scores:{}'.format(scores))
print('Average Cross-validation score:{:.2f}'.format(scores.mean()))

运行结果如下：

Cross-validation scores:[1.         1.         1.         1.         0.66666667]
Average Cross-validation score:0.93

采用交叉验证后，可以看到不同模型得分不一样，平均精度在93%。也就是说，有93%的把握可以认为分类器给出的分类结果是正确的，这点与一个模型得分有较大差异。通过该种办法提高了数据使用效能，提高了模型泛化的能力。

2.2 更有效数据划分

2.2.1 交叉验证分离器

如果想对数据划分进行更细微的控制，可以使用交叉验证分离器对cv参数进行设置。通过设置参数后，模型训练得分会大不相同。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
df1 = pd.read_csv('E:\PYTHON\ground_feature0.csv') #读取特征向量
data = df1.values
X = data[:,0:2] #构建要分割的数据,前两列
y = data[:,2] #构建分类目标
#分割数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=10)
gf_tree = DecisionTreeClassifier(criterion='entropy',max_depth=3,random_state=0)
gf_tree.fit(X_train,y_train)

kfold = KFold(n_splits=5)
score_1 = cross_val_score(gf_tree,X_train,y_train,cv=kfold) #设置cv参数
print('Cross-validation scores:{}'.format(score_1))
print('Average Cross-validation score:{:.2f}'.format(score_1.mean()))

运行结果如下：

Cross-validation scores:[0.25       1.         0.66666667 1.         0.66666667]
Average Cross-validation score:0.72

由运行结果可知，最差的模型得分为0.25,5个模型的平均得分为0.72。

2.2.2 打乱交叉验证

在指定求取一个分类模型时，在样本空间设定训练数据集和测试数据集比例，训练一次，然后指定重复模型建立的次数。这种方法与K折交叉验证方法在数据划分上有很大区别。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.model_selection import ShuffleSplit
df1 = pd.read_csv('E:\PYTHON\ground_feature0.csv') #读取特征向量
data = df1.values
X = data[:,0:2] #构建要分割的数据,前两列
y = data[:,2] #构建分类目标
#分割数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=10)
gf_tree = DecisionTreeClassifier(criterion='entropy',max_depth=3,random_state=0)
gf_tree.fit(X_train,y_train)
shuffle_split = ShuffleSplit(test_size=.3,train_size=.7,n_splits=5)
#score_2 = cross_val_score(gf_tree,X_train,y_train,cv=shuffle_split)
score_2 = cross_val_score(gf_tree,X,y,cv=shuffle_split)
print('Cross-validation scores:{}'.format(score_2))
print('Average Cross-validation score:{:.2f}'.format(score_2.mean()))

运行结果如下：

Cross-validation scores:[1.         1.         0.85714286 0.57142857 1.        ]
Average Cross-validation score:0.89

2.3 模型参数优化

2.3.1 网络搜索

参数寻优是算法设计中必须要有的环节。sklearn包中提供网络搜索方法，基本可以解决参数最优化问题。该方法将可能的参数进行组合，以查询不同组合参数下的分类器性能。

例如，单相接地故障核——SVM参数网格搜索程序如下:

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
df1 = pd.read_csv('E:\PYTHON\ground_feature0.csv') #读取特征向量
data = df1.values
X = data[:,0:2] #构建要分割的数据,前两列
y = data[:,2] #构建分类目标
#分割数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=10)
print('Size of training set: {} size of test set: {}'.format(X_train.shape[0],X_test.shape[0]))
best_score=0
for gamma in [0.001,0.01,0.1,1,10,100,500]:
    for C in [0.001,0.01,0.1,1,10,100,500]:
        #gamma和C参数影响大，对每种参数组合都训练一个模型
        gf_svm = SVC(kernel='rbf',random_state=0,gamma=gamma,C=C)
        gf_svm.fit(X_train,y_train)
        #测试集评估SVC
        score = gf_svm.score(X_test,y_test)
        if score>best_score:
            best_score=score
            parameters = {'C':C,'gamma':gamma}
print('Best score :{:.2f}'.format(best_score))
print('Best parameters :{}'.format(parameters))

运行结果如下：

Size of training set: 16 size of test set: 6
Best score :1.00
Best parameters :{'C': 100, 'gamma': 0.1}

这样，通过组合搜索，可以知道gf_svm=SVC(kernel='rbf',random_state=0,gamma=0.1,C=100)能够创建更好的分类模型。

2.3.2 交叉验证网络搜索

为了提高数据使用效率，提高分类模型泛化能力，并能够得到最优的参数性能，可以联合网络搜索和交叉验证两个技术一起使用。

交叉验证网络搜索：

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score
df1 = pd.read_csv('E:\PYTHON\ground_feature0.csv') #读取特征向量
data = df1.values
X = data[:,0:2] #构建要分割的数据,前两列
y = data[:,2] #构建分类目标
#分割数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=10)
print('Size of training set: {} size of test set: {}'.format(X_train.shape[0],X_test.shape[0]))
best_score=0
for gamma in [0.001,0.01,0.1,1,10,100,500]:
    for C in [0.001,0.01,0.1,1,10,100,500]:
        #gamma和C参数影响大，对每种参数组合都训练一个模型
        gf_svm = SVC(kernel='rbf',random_state=0,gamma=gamma,C=C)
        #执行交叉验证，求取5个模型的得分
        scores = cross_val_score(gf_svm, X, y, cv=5)
        #求平均分
        score = np.mean(scores)
        if score>best_score:
            best_score=score
            parameters = {'C':C,'gamma':gamma}
#用最优参数构建模型，并训练模型，求取最后模型泛化得分
svm = SVC(**parameters)
svm.fit(X_train,y_train)
print('Best_Model score :{:.2f}'.format(svm.score(X_test,y_test)))

运行结果如下：

Size of training set: 16 size of test set: 6
Best_Model score :1.00

在建立分类模型之前，数据一般还需要预处理，预处理后可以提高模型的性能。MinMaxScaler类可以实现数据缩放。

利用MinMaxScaler类的数据缩放预处理：

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.preprocessing import MinMaxScaler
df1 = pd.read_csv('E:\PYTHON\ground_feature0.csv') #读取特征向量
data = df1.values
X = data[:,0:2] #构建要分割的数据,前两列
y = data[:,2] #构建分类目标
#分割数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=10)
#计算数据的最小最大值
scaler = MinMaxScaler().fit(X_train)
#对训练数据进行缩放
X_train_scaled = scaler.transform(X_train)
gf_svm = SVC()
gf_svm.fit(X_train_scaled,y_train)
X_test_scaled = scaler.transform(X_test)
print('Test_Model score :{:.2f}'.format(gf_svm.score(X_test_scaled,y_test)))

运行结果如下：

Test_Model score :0.83

此模型效果尚不算佳，一般情况下，数据集过小会导致这种情况出现。

2.3.3 管道使用

可以构建管道，将数据集缩放与训练模型连接起来，形成一个新的整体。

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import Pipeline
df1 = pd.read_csv('E:\PYTHON\ground_feature0.csv') #读取特征向量
data = df1.values
X = data[:,0:2] #构建要分割的数据,前两列
y = data[:,2] #构建分类目标
#分割数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=10)
#计算数据的最小最大值
scaler = MinMaxScaler().fit(X_train)
#对训练数据进行缩放
X_train_scaled = scaler.transform(X_train)
pipe = Pipeline([("scaled",MinMaxScaler()),("gf_svm",SVC())])
pipe.fit(X_train,y_train)
print('Pipe_Model score :{:.2f}'.format(pipe.score(X_test,y_test)))

运行结果如下：

Pipe_Model score :0.83

2.4 主成分分析

主成分分析（principal components analysis,PCA）是一种无监督算法，常用来对数据进行可视化、压缩处理。Python中使用“from sklearn.decomposition import PCA”语句导入PCA模块进行主成分分析，主要参数解释如下：

（1）n_components：指定PCA降维后的特征维度数目；

（2）whiten：指定是否进行白化；

（3）svd_solver指定奇异值分解的方法，可选值有4个，{'auto','full','arpack','randomized'}

例2.4.1，使用自带数据集葡萄酒数据集进行主成分分析并将数据集可视化：

from sklearn.datasets import load_wine
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

#加载葡萄酒数据集
wine_data = load_wine()
X = wine_data['data']
y = wine_data['target']

#利用StandardScaler缩放数据集，使特征方差均为1
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)

#主成分分析
#保留前两个主成分
pca = PCA(n_components=2)

#将数据拟合PCA模型
pca.fit(X_scaled)

#将数据变化到前两个主成分的方向
X_pca = pca.transform(X_scaled)
print('Original shape: {}'.format(str(X.shape)))
print('Reduced shape: {}'.format(str(X_pca.shape)))

#主成分分析前数据集的二维散点图
for c,i,target_name in zip("rgb",[0,1,2],wine_data.target_names):
    plt.scatter(X[y==i,0],X[y==i,1],c=c,label = target_name)
plt.xlabel(wine_data.feature_names[0])
plt.ylabel(wine_data.feature_names[1])
plt.legend(loc='best')
plt.show()

#利用前两个主成分绘制数据集的二维散点图
for c,i,target_name in zip("rgb",[0,1,2],wine_data.target_names):
    plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], c=c, label=target_name)
plt.xlabel('First principal component')
plt.ylabel('Second principal component')
plt.legend(loc='best')
plt.show()

运行结果如下：

Original shape: (178, 13)
Reduced shape: (178, 2)

 主成分分析前数据集的二维散点图

 利用前两个主成分绘制数据集的二维散点图

例2.4.1，使用乳腺癌数据集进行PCA降维处理并调用逻辑回归对数据进行拟合：

from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap

#加载葡萄酒数据集
cancer_data = load_breast_cancer()
X = cancer_data['data']
y = cancer_data['target']

#分割数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=0)
lr = LogisticRegression()
lr.fit(X_train,y_train)

#利用StandardScaler缩放数据集，使特征方差均为1
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.fit_transform(X_test)

#主成分分析
#保留前两个主成分
pca = PCA(n_components=2)

#逻辑回归拟合模型
lr = LogisticRegression()
X_train_pca = pca.fit_transform(X_train_scaled)
X_test_pca = pca.fit_transform(X_test_scaled)
lr.fit(X_train_pca,y_train)

def plot_decision_regions(X,y,classifier,test_idx=None,resolution=0.02):#两类分类曲线绘图函数定义
    #setup marker generator and color map
    markers = ('s','x','o','^','v')
    colors = ('red','blue','lightgreen','gray','cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    #plot the decision surface
    x1_min,x1_max = X[:,0].min()-1,X[:,0].max()+1
    x2_min,x2_max = X[:,1].min()-1,X[:,1].max()+1
    xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),np.arange(x2_min,x2_max,resolution))
    Z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1,xx2,Z,alpha=0.4,cmap=cmap)
    plt.xlim(xx1.min(),xx1.max())
    plt.ylim(xx2.min(),xx2.max())
    #plot all sample
    X_test,y_test = X[test_idx,:],y[test_idx]
    for idx,cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y==cl,0],y=X[y==cl,1],alpha=0.8,c=cmap(idx),marker=markers[idx],label=cl)

#对训练数据集和测试数据集分类结果可视化

plot_decision_regions(X_train_pca,y_train,classifier=lr)
plt.title('Training Result')
plt.xlabel('First principal component')
plt.ylabel('Second principal component')
plt.legend(cancer_data.target_names,loc='best')
plt.show()


plot_decision_regions(X_test_pca,y_test,classifier=lr)
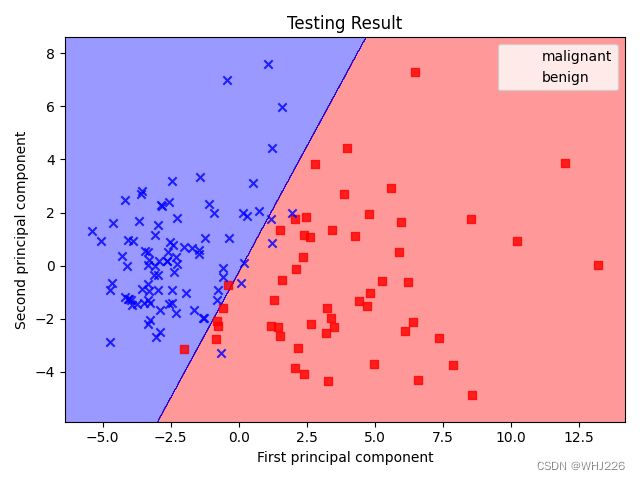
plt.title('Testing Result')
plt.xlabel('First principal component')
plt.ylabel('Second principal component')
plt.legend(cancer_data.target_names,loc='best')
plt.tight_layout()
plt.show()

运行结果如下：

 

 良性用‘×’表示，恶性用红色方框表示，经过PCA分析后，恶性在图中更加分散。

2.5 流形学习

流形学习（manifold learning）也是一种降维算法，一样可以用于变换数据，将数据维数降维或数据可视化。但他和PCA不同，PCA是一种线性算法，不能解释特征之间的复杂的多项式关系，而流形学习的基本思想是将高维度原始空间中的某些特征结构通过非线性降维方法在低维度中仍然能够保持。这里介绍一种比较好的算法——t-分布随机邻域嵌入（t-distributed stochastic neighbr embedding,t-SNE）算法。该算法是基于在邻域图上的随机游走的概率分布来找到数据内部的结构。

t-SNE算法的使用：

from sklearn.datasets import load_digits
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt

#导入手写字体学习数据
digits = load_digits()
X = digits.data
y = digits.target

#使用t-SNE算法构建模型
tsne = TSNE(n_components=2,init='pca',random_state=0)
X_tsne = tsne.fit_transform(X)

#绘制散点图
plt.figure()
c=['red','green','blue','yellow','purple','black']
for i,color in zip(range(len(X)),c):
    p=X[y==i]
    plt.scatter(X_tsne[y==i,0],X_tsne[y==i,1],c=color,label=digits.target_names[i])
plt.legend()
plt.xlabel('t-SNE feature 0')
plt.ylabel('t-SNE feature 1')
plt.show()

运行结果如下：