【图解RSA加密算法】RSA非对称密码算法的Python实现保姆级教程 | 物联网安全 | 信息安全

系列索引：【图解安全加密算法】加密算法系列索引 Python保姆级实现教程 | 物联网安全 | 信息安全

一、什么是RSA加密算法

RSA加密算法是一种非对称加密算法。在公开密钥加密和电子商业中RSA被广泛使用。RSA是1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。RSA就是他们三人姓氏开头字母拼在一起组成的。

对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。假如有人找到一种快速因数分解的算法的话，那么用RSA加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA钥匙才可能被强力方式解破。世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长，用RSA加密的信息实际上是不能被解破的。

RSA公开密钥密码体制。所谓的公开密钥密码体制就是使用不同的加密密钥与解密密钥，是一种“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制。RSA算法是第一个能同时用于加密和数字签名的算法，也易于理解和操作。RSA是被研究得最广泛的公钥算法，从提出到现今的四十多年里，经历了各种攻击的考验，逐渐为人们接受，截止2017年被普遍认为是最优秀的公钥方案之一。

二、RSA算法原理

三、具体要求

1. p、q可由用户输入或系统自动生成，当用户输入时要判断p和q是否为质数
2. e、d根据算法要求由系统自动生成
3. 加密时要注意明文长度M

四、代码实现

1.公钥、私钥生成实现

   def generate(self):
        p, q = int(input("请输入素数p的值：")),  int(input("请输入素数q的值："))
        lambdan = self.lcm(p - 1, q - 1)
        e = 0
        while not self.is_prime(e):
            e = random.randint(2, lambdan - 1)
        d = [0]
        self.ex_gcd(e, lambdan, [0], d, [0])
        d = d[0] % lambdan
        print("公钥PU=[e={},n={}]".format(e, p*q))
        print("私钥PR=[d={},n={}]".format(d, p*q))
        return {
            'n': p * q,
            'e': e,
            'd': d,
        }

2. RSA加解密算法实现

import random

class RSA:
    def is_prime(self, n):
        if n <= 3:
            return n > 1
        elif (n % 2 == 0) or (n % 3 == 0):
            return False
        i = 5
        while i * i <= n:
            if (n % i == 0) or (n % (i + 2) == 0):
                return False
            i += 6
        return True

    def gcd(self, a, b):
        return a if b == 0 else self.gcd(b, a % b)

    def lcm(self, a, b):
        return a // self.gcd(a, b) * b
    def ex_gcd(self, a, b, d, x, y):
        if b == 0:
            d[0], x[0], y[0] = a, 1, 0
        else:
            self.ex_gcd(b, a % b, d, y, x)
            y[0] -= a // b * x[0]

    def quick_power(self, a, b, mod):
        res = 1
        while b != 0:
            if (b & 1) == 1:
                res = (res * a) % mod
            a = a * a % mod
            b >>= 1
        return res

    def generate(self):
        p, q = int(input("请输入素数p的值：")),  int(input("请输入素数q的值："))
        lambdan = self.lcm(p - 1, q - 1)
        e = 0
        while not self.is_prime(e):
            e = random.randint(2, lambdan - 1)
        d = [0]
        self.ex_gcd(e, lambdan, [0], d, [0])
        d = d[0] % lambdan
        print("公钥PU=[e={},n={}]".format(e, p*q))
        print("私钥PR=[d={},n={}]".format(d, p*q))
        return {
            'n': p * q,
            'e': e,
            'd': d,
        }

    def encrypt(self, m, e, n):
        c = self.quick_power(m, e, n)
        return c

    def dencypt(self, c, d, n):
        m = self.quick_power(c, d, n)
        return m

def show():
    print("="*25)
    print(" "*5+"{}".format("欢迎进入RSA算法"))
    print(" "*5+"1--加密")
    print(" "*5+"2--解密")
    print(" "*5+"3--退出")
    print("="*25)
    choose = int(input("请输入要选择的功能号："))
return choose

if __name__ == "__main__":
    msg = input("请输入初始明文：")
    rsa1 = RSA()
    rsa2 = RSA()
    keys = rsa1.generate()
    c, m = [], []
    choose = show()
    while choose != 3:
        if choose == 1:
            for i in range(len(msg)):
                c.append(rsa2.encrypt(m=ord(msg[i]), e=keys['e'], n=keys['n']))
            cc = "".join(str(c))
            print("密文是：{}".format(cc))
        elif choose == 2:
            for i in range(len(msg)):
                m.append(chr(rsa1.dencypt(c[i], d=keys['d'], n=keys['n'])))
            ming = "".join(m)
            print("明文：{}".format(ming))
        choose = show()

五、实验结果与心得体会

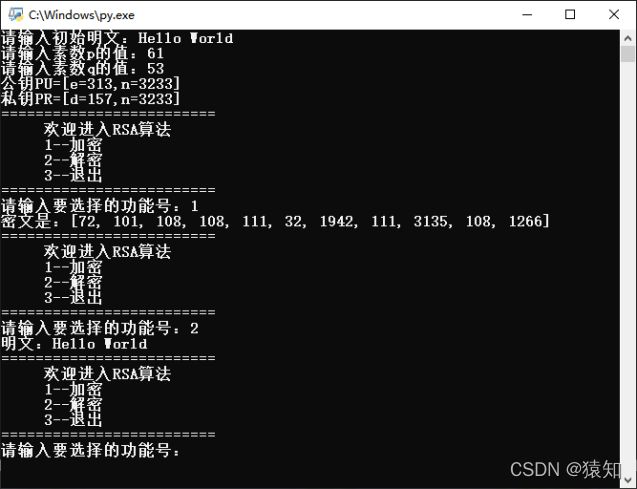
首先这次实验的难度不是特别大，对于RSA加密和解密的过程我依旧使用Python进行实现，有了AES加密算法的处理经验和基础，在实现这次加密过程中几乎很顺利，在这个过程中我也查阅了一些不熟悉的知识点，如字符串和阿斯克码的转化，期初我是想直接把明文一次性转换，但遇到了一些问题，想到老师讲的逐个转换，我于是转变思路顺利完成实验设计，在界面设计上也尽可能向老师给的示例看齐，加油！

图解安全加密算法系列持续更新，欢迎点赞收藏＋关注

上一篇：【图解SHA1杂凑算法】SHA1杂凑算法的Python实现保姆级教程 | 物联网安全 | 信息安全
下一篇：【图解AES加密算法】AES算法的Python实现 | Rijndael-128 | 对称加密 | 物联网安全

本人水平有限，文章中不足之处欢迎下方评论区批评指正~

如果感觉对你有帮助，点个赞 支持一下吧 ~

不定期分享 有趣、有料、有营养内容，欢迎 订阅关注 我的博客 ，期待在这与你相遇 ~