手搭深度推荐模型(四) NFM

本文是笔者参与datawhale组织的深度推荐模型组队学习的分享，学习内容见本链接 ，本文中所指的教程即该链接中的相应文件。

一、概念

为了在稀疏条件下有更好的预测性能，2017年何向南教授等人在SIGIR会议上提出了NFM(Neural Factorization Machines)模型。传统的FM及其改进的FFM本质是一个二阶特征交叉模型，尽管其处理稀疏向量的能力很好，但是由于FM的特征交叉是一种暴力组合，无法扩展到更高阶，因此限制了FM的表达能力。因此作者尝试使用非线性表达能力强的MLP部分代替了原FM中的二阶隐向量内积的部分，使其有更强的表达能力。
FM表达式
$${\hat{y}}_{FM}(x)=w_0+\sum _{i=1}^N{w}_i{x}_i+\sum _{i=1}^N\sum _{j=i+1}^N{v}_i^T{v}_j{x}_i{x}_j$$
NFM表达式
$${\hat{y}}_{NFM}(\mathbf{x})=w_0+\sum _{i=1}^n{w}_i{x}_i+f(\mathbf{x})$$
另外，NFM也借鉴了Wide&Deep模型的思想，分成了wide和deep两部分，NFM对其deep部分作出了改进，整体的网络结构如图所示(图片转自datawhale)。

其中，作者改进了Deep部分，主要是创造了一个Bi-Interaction Pooling层来将FM的M×K的矩阵（M为稀疏特征数量，K为稀疏特征Embedding之后的尺寸）对接到MLP模块，交给MLP模块进行高阶非线性的交叉。改进的Deep部分如图所示。

为了将FM的输出与MLP层相连，使整个网络能够正常前向传播、后向传播，NFM在Bi-Interaction Pooling中使用了如下函数
$$f_{BI}\left({\mathcal{V}}_x\right)=\sum _{i=1}^n\sum _{j=i+1}^n{x}_i{\mathbf{v}}_i\odot x_j{\mathbf{v}}_j$$
其中$\odot$表示两个向量点对点的元素积操作。其他层的操作与其他网络相比没有改变，不做特别说明。

二、NFM相对于其他模型的改进

1. FM视角

FM本身就是处理稀疏特征非常好的模型，但由于计算量的限制不易表达三阶及以上的交叉特征，因此仍有提升空间。从FM视角看NFM的改进，主要在于FM的输出是一个标量，而NFM的Bi-Interaction Pooling层的输出不是标量，因为NFM使用了元素积而没有用点积，因此其输出的矩阵可以继续被MLP层学习。

2. Wide&Deep视角

Wide&Deep模型的提出使推荐系统能够兼顾泛化能力与记忆能力。前面所提到的DeepFM通过在Wide部分结合了FM，加强了浅层网络部分的特征组合的能力。而本文的NFM模型则是将FM应用在了Deep层，使Deep层对于稀疏向量的处理有了更好的表达。

3. Embedding + MLP视角

从DeepCrossing模型开始，embedding+mlp就成了深度推荐系统的标配，但是通常的MLP层的输入都是一阶特征，特征交叉是交给MLP来做的，而NFM则是预先做好了二阶的交叉，再交给MLP，使MLP的输入端有了更高阶的特征，一定程度为MLP减负。不过作者在这里也提到，他们做了实验，MLP为0层（即原始的FM）到4层，可以看出在论文中比对的两个数据集中，单个隐层效果较好，这既说明了NFM可以比FM更有效，也说明不易让MLP对特征进行过于复杂的交叉。

三、代码复现

代码

这里使用了采样了200个样本的Criteo数据集，我没有实现完整的NFM，只实现了Deep部分，因为NFM改进了wide&deep的deep部分。
Bi-Interaction Pooling层的实现借鉴了公式
$$f_{BI}\left({\mathcal{V}}_x\right)=\sum _{i=1}^n\sum _{j=i+1}^n{x}_i{\mathbf{v}}_i\odot x_j{\mathbf{v}}_j=\frac{1}{2}\left[{\left(\sum _{i=1}^n{x}_i{\mathbf{v}}_i\right)}^2-\sum _{i=1}^n{\left(x_i{\mathbf{v}}_i\right)}^2\right]$$

class bi_interaction_pooling(Layer):
    def __init__(self):
        super(bi_interaction_pooling, self).__init__()

    def call(self, inputs):
        x = inputs
        # 和的平方 - 平方的和
        x = 0.5 * (tf.square(tf.reduce_sum(x, axis=1)) - tf.reduce_sum(tf.square(x), axis=1))
        return x

def NFM(sparse_fea,
        embedding_size=32,
        num_hidden_layers=1,
        if_bn=False,
        if_dropout=True,
        dropout_factor=[0.5]):
    inputs_dict = {}
    for fea in sparse_fea:
        inputs_dict[fea] = Input(shape=(1,), name=fea)
    embedded = []
    for fea in inputs_dict:
        embedded.append(Embedding(sparse_fea[fea], embedding_size)(inputs_dict[fea]))
    x = Concatenate(axis=1)(embedded)
    x = bi_interaction_pooling()(x)
    if if_bn:
        x = BatchNormalization()(x)
    for i in range(num_hidden_layers):
        x = Dense(32, activation='relu')(x)
        if if_dropout:
            x = Dropout(dropout_factor[i])(x)
    output = Dense(1, activation='sigmoid')(x)
    return Model(inputs_dict.values(), output)

keras绘制deep部分的模型:

实验

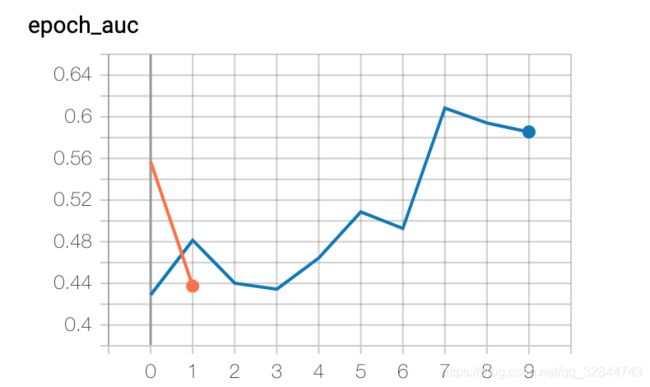
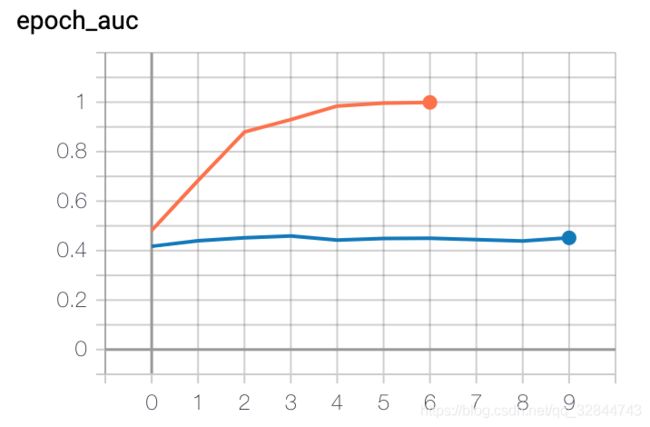
由于样本量只有200，使用BatchNormalization的时候效果不好，实验时发现过拟合情况比较严重，因此设置了较高的Dropout比例(0.5)，分别在hidden unit=0,1,2,3时实验，hidden unit=0时即为FM。下图为TensorBoard的训练过程图，橘色为训练集的AUC，蓝色曲线为验证集的AUC

hidden unit = 0

hidden unit = 1

hidden unit = 2

hidden unit = 3

四、思考

Q1. NFM中的特征交叉与FM中的特征交叉有何异同，分别从原理和代码实现上进行对比分析
原理
相同点: NFM和FM都生成了M×K(M为特征数量，K为矩阵分解的维度，也即单个特征Embedding后的维度）的矩阵，而且生成矩阵都使用了梯度下降来求解。
不同点: FM生成矩阵后对其求和，故其输出是一个标量。而NFM只作元素积，不求和，故其输出是矩阵，继续交给MLP层训练。另外，FM训练时用类似矩阵分解的方法，只训练自己的特征矩阵，是独立的。而NFM的权重随整个网络更新。
代码
这里对比教程中DeepFM模型的FM实现部分和NFM的Bi-Interaction Pooling部分，可以看出NFM相对于FM的区别。
FM的实现如图所示：

class FM_Layer(Layer):
    def __init__(self):
        super(FM_Layer, self).__init__()

    def call(self, inputs):
        # 优化后的公式为： 0.5 * 求和（和的平方-平方的和）  =>> B x 1
        concated_embeds_value = inputs # B x n x k

        square_of_sum = tf.square(tf.reduce_sum(concated_embeds_value, axis=1, keepdims=True)) # B x 1 x k
        sum_of_square = tf.reduce_sum(concated_embeds_value * concated_embeds_value, axis=1, keepdims=True) # B x1 xk
        cross_term = square_of_sum - sum_of_square # B x 1 x k
        cross_term = 0.5 * tf.reduce_sum(cross_term, axis=2, keepdims=False) # B x 1

        return cross_term

    def compute_output_shape(self, input_shape):
        return (None, 1)

NFM的实现如图所示:

class BiInteractionPooling(Layer):
    def __init__(self):
        super(BiInteractionPooling, self).__init__()

    def call(self, inputs):
        # 优化后的公式为： 0.5 * （和的平方-平方的和）  =>> B x k
        concated_embeds_value = inputs # B x n x k

        square_of_sum = tf.square(tf.reduce_sum(concated_embeds_value, axis=1, keepdims=False)) # B x k
        sum_of_square = tf.reduce_sum(concated_embeds_value * concated_embeds_value, axis=1, keepdims=False) # B x k
        cross_term = 0.5 * (square_of_sum - sum_of_square) # B x k

        return cross_term

    def compute_output_shape(self, input_shape):
        return (None, input_shape[2])

可以看出，FM多了如下一行:

cross_term = 0.5 * tf.reduce_sum(cross_term, axis=2, keepdims=False) # B x 1

NFM的Bi-Interaction Pooling层这里的输出是Batchsize × 1，而FM里的输出是Batchsize × K，因此验证了前面所说的，FM会将输出求和，因为求和之后要用梯度更新FM的参数，而NFM则是将输出交给MLP，因此不必求和。

Q2.在学习了NFM之后我还有一个疑惑，我认为NFM的主要改进就是原本MLP层的输入都是一阶特征，而NFM则是给了MLP二阶特征作为输入。我的疑惑是，MLP本身也具有很好的非线性高阶拟合能力，为什么NFM让FM来代替MLP来做二阶特征交叉效果会更好呢，是在通用情况下FM的二阶特征交叉能力都强于MLP，还是说仅在某些情况下？欢迎各位留言为我解惑~

五、参考文献

• NFM论文
• FunRec
• 王喆 - 《深度学习推荐系统》