层次聚类算法_R 无监督聚类算法（1）K-means和层次聚类

首先我们要解决几个问题

聚类算法主要包括哪些算法？

主要包括：K-means、DBSCAN、Density Peaks聚类（局部密度聚类）、层次聚类、谱聚类。

什么是无监督学习？

• 无监督学习也是相对于有监督学习来说的，因为现实中遇到的大部分数据都是未标记的样本，要想通过有监督的学习就需要事先人为标注好样本标签，这个成本消耗、过程用时都很巨大，所以无监督学习就是使用无标签的样本找寻数据规律的一种方法

• 聚类算法就归属于机器学习领域下的无监督学习方法。 无监督学习的目的是什么呢？

• 可以从庞大的样本集合中选出一些具有代表性的样本子集加以标注，再用于有监督学习

• 可以从无类别信息情况下，寻找表达样本集具有的特征

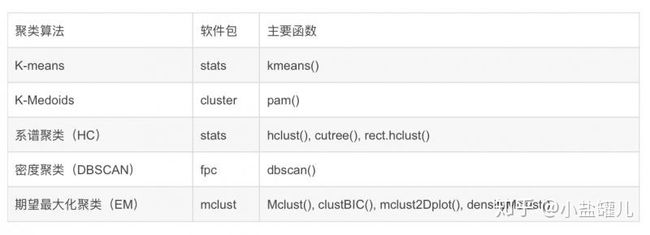
R中有哪些无监督学习的包？

---

# 需要用到的数据集和包
library(readr)
library(dplyr)
library(ggplot2)

我们有的数据集是kaggle中的pokemon dataset

# 简单查看一下数据
pokemon_raw = read_csv('Pokemon.csv')
head(pokemon_raw)
## # A tibble: 6 x 13
##     `#`                  Name `Type 1` `Type 2` Total    HP Attack Defense
##                                   
## 1     1             Bulbasaur    Grass   Poison   318    45     49      49
## 2     2               Ivysaur    Grass   Poison   405    60     62      63
## 3     3              Venusaur    Grass   Poison   525    80     82      83
## 4     3 VenusaurMega Venusaur    Grass   Poison   625    80    100     123
## 5     4            Charmander     Fire        309    39     52      43
## 6     5            Charmeleon     Fire        405    58     64      58
## # ... with 5 more variables: `Sp. Atk` , `Sp. Def` ,
## #   Speed , Generation , Legendary 
# 只选择连续型变数来做聚类
pokemon = pokemon_raw %>% 
  select(6:11)
head(pokemon)
## # A tibble: 6 x 6
##      HP Attack Defense `Sp. Atk` `Sp. Def` Speed
##                   
## 1    45     49      49        65        65    45
## 2    60     62      63        80        80    60
## 3    80     82      83       100       100    80
## 4    80    100     123       122       120    80
## 5    39     52      43        60        50    65
## 6    58     64      58        80        65    80

k-means

k均值聚类算法（k-means clustering algorithm）是一种迭代求解的聚类分析算法，其步骤是随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。

优点：1.有效率且不容易受到初始值的影响。

缺点：1.不能处理非球形簇；2.不能处理不同尺寸，不懂密度的簇；3.离群值会有较大干扰（一定要在预处理时剔除掉

R 内置了一个函数kmeans可以用做聚类分析 kmeans中第一个参数是dataset。centers是中心点选择参数，表示聚成几类。iter.max是迭代次数的参数，即迭代次数，不写的话默认是10次。 algorithm是算法选择的参数，算法有”Hartigan-Wong”, “Lloyd”, “Forgy”,”MacQueen”四种。

# Initialize total within sum of squares error: wss
wss = 0
# 分成1至15个簇的结果
for (i in 1:15) {
  # 先创建一个模型: km.out
  km.out = kmeans(pokemon, centers = i, nstart = 20, iter.max = 50)
  # 保存每个簇的组内距离平方和
  wss[i] = km.out$tot.withinss
}

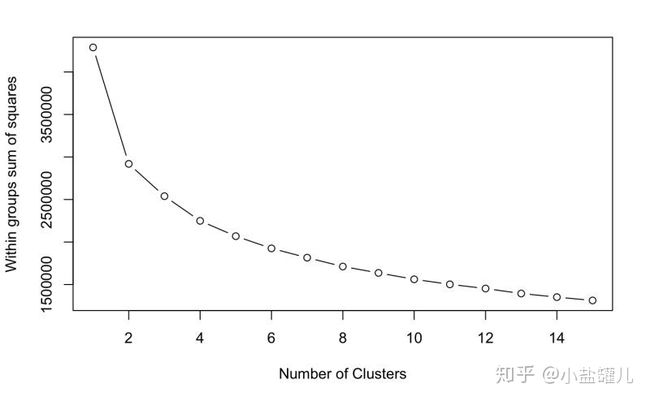
# 结果可视化，x轴是分群数，y轴是wss，每个簇内部的距离平方和，表示该簇的紧密程度。
plot(1:15, wss, type = "b", 
     xlab = "Number of Clusters", 
     ylab = "Within groups sum of squares")

# 根据上图我们选择分四组
k = 4

# 建立一个4个群的模型
km.pokemon <- kmeans(pokemon, centers = k, nstart = 20, iter.max = 50)

# 画出Defense vs. Speed这两个变数的分群结果
# 因为只能画出二维的状态，所以有很多是重叠的部分
plot(pokemon[, c("Defense", "Speed")],
     col = km.pokemon$cluster,
     main = paste("k-means clustering of Pokemon with", k, "clusters"),
     xlab = "Defense", ylab = "Speed")

Hierarchical clustering层次聚类

层次法（Hierarchicalmethods）先计算样本之间的距离。每次将距离最近的点合并到同一个类。然后，再计算类与类之间的距离，将距离最近的类合并为一个大类。不停的合并，直到合成了一个类。其中类与类的距离的计算方法有：最短距离法，最长距离法，中间距离法，类平均法等。比如最短距离法，将类与类的距离定义为类与类之间样本的最短距离。

层次聚类算法根据层次分解的顺序分为：自下底向上和自上向下，即凝聚的层次聚类算法和分裂的层次聚类算法（agglomerative和divisive），也可以理解为自下而上法（bottom-up）和自上而下法（top-down）。自下而上法就是一开始每个个体（object）都是一个类，然后根据linkage寻找同类，最后形成一个“类”。自上而下法就是反过来，一开始所有个体都属于一个“类”，然后根据linkage排除异己，最后每个个体都成为一个“类”。这两种路方法没有孰优孰劣之分，只是在实际应用的时候要根据数据特点以及你想要的“类”的个数，来考虑是自上而下更快还是自下而上更快。

至于根据Linkage判断“类”的方法就是最短距离法、最长距离法、中间距离法、类平均法等等（其中类平均法往往被认为是最常用也最好用的方法，一方面因为其良好的单调性，另一方面因为其空间扩张/浓缩的程度适中）。为弥补分解与合并的不足，层次合并经常要与其它聚类方法相结合，如循环定位。

优点：1.距离和规则的相似度容易定义，限制少；2.不需要预先制定聚类数；3.可以发现类的层次关系；4.可以聚类成其它形状

缺点：1.计算复杂度太高；2.奇异值也能产生很大影响；3.算法很可能聚类成链状

# 查看每列 means
colMeans(pokemon)
##       HP   Attack  Defense  Sp. Atk  Sp. Def    Speed 
## 69.25875 79.00125 73.84250 72.82000 71.90250 68.27750

# 查看每列 standard deviations
apply(pokemon, 2, sd)
##       HP   Attack  Defense  Sp. Atk  Sp. Def    Speed 
## 25.53467 32.45737 31.18350 32.72229 27.82892 29.06047

# 将数据标准化
pokemon.scaled <- scale(pokemon)

聚类集合间的距离method，也就是linkage（连接方法linkage指的是衡量簇与簇之间的远近程度的方法)

最长距离法(complete) 默认；最短距离法(single) ；平均距离法(average)；重心法(centroid)

# 建立 hierarchical clustering 模型: hclust.pokemon
# dist(pokemon.scaled)先需要将数据转化为两点间的距离
hclust.pokemon <- hclust(dist(pokemon.scaled), method = "complete")
# HitPoints         Attack        Defense  SpecialAttack SpecialDefense          Speed 
#  69.25875       79.00125       73.84250       72.82000       71.90250       68.27750 
# HitPoints         Attack        Defense  SpecialAttack SpecialDefense          Speed 
#  25.53467       32.45737       31.18350       32.72229       27.82892       29.06047
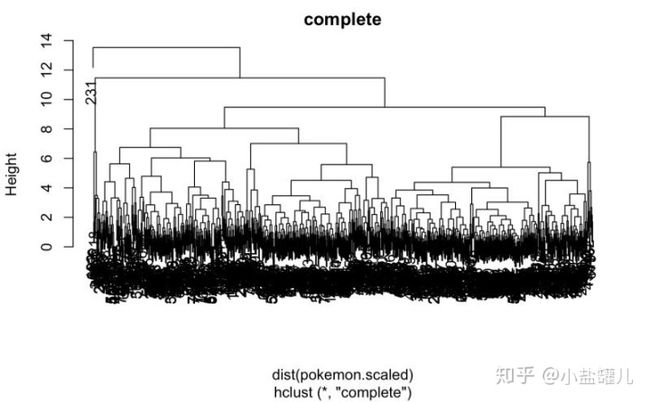
# 可视化 hclust.pokemon
plot(hclust.pokemon, main = "complete")

比较 kmeans() and hclust()

# Apply cutree() to hclust.pokemon: cut.pokemon
cut.pokemon <- cutree(hclust.pokemon, k = 3)

# Compare methods
table(km.pokemon$cluster, cut.pokemon)

# cut.pokemon
#      1   2   3
#  1 283   0   0
#  2 114   0   1
#  3 277  11   0
#  4 114   0   0

这是个令人比较困惑的例子，可以看到kmeans()将观测结果分成了比较明显的四簇，但是hclust()几乎把所有观测结果都放在了一个簇中。我们虽然期待可以分成较多的分散集群，但是不能单单因为这个就得出哪个比较好的结论。

欢迎关注【数据小盐罐儿】一个很“咸”的数据科学公众号，不定期分享一些有趣好玩的项目以及大量的学习资源