马科维茨模型的实例验证与思考（含Python代码）

目录

马科维兹模型简述

一、原理

二、相关公式

实例验证

一、方法选择

二、思路

①假设

②设定

③注意

三、实践

①数据准备

②用蒙特卡洛方法计算组合权重

③把有效前沿组合选出来

④测试时间段股票表现情况

 ⑤有效前沿组合在测试时间段的收益情况

四、思考

---

马科维茨模型简述

一、原理

        马科维茨均值-方差组合模型简单来讲就是想做出在特定收益率水平下方差最小的投资组合。

        隐含条件：①投资多个股票，分散风险；②股票间的相关系数较低。

二、相关公式

       收益向量 

        期望向量

        方差向量

        协方差阵

        权重向量

        组合收益

        组合期望

        组合方差

具体参考：金融数学 第三章 均值方差证券投资组合选择模型 - MBA智库文档

---

实例验证

一、方法选择

        求组合有效前沿可用二次规划求解，本例选用蒙特卡洛模拟，即投放大量随机算子进行模拟。

二、思路

        利用一段时间的数据计算出投资组合有效前沿权重，以此权重计算后续一段时间的收益情况。

①假设

        选取的各股票在计算时间段的收益为正，假设其在后续一段时间有持续上涨的趋势。

②设定

        计算时间段为3个月，测试（预测）时间段为最近（约1个半月）。

③注意

        选取的股票之间需要低相关性，这次才能较好地分散风险。

三、实践

①数据准备

        股票是随意找的，符合假设就ok，不构成投资建议。

如果想要自定义的程序，请私信，谢谢！

# 准备股票代码
stock_list = ['600176.SH',\
              '002594.SZ',\
              '002080.SZ',\
              '000733.SZ',\
              '600373.SH',\
              '300142.SZ',\
              '300498.SZ',\
              '002625.SZ',\
              '000519.SZ',\
              '603290.SH',\
              '300502.SZ']

# 设定准备数据的时间段
# 用作计算的数据时间段
start_date_cal = '20210701'
end_date_cal = '20210930'
# 用作测试的数据时间段
start_date_test = '20211001'
end_date_test = '20211115'

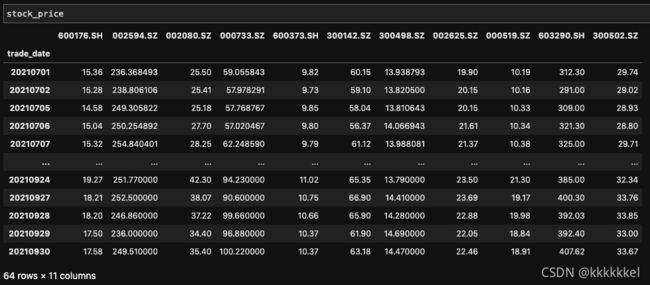
# 获得各股票的价格
stock_price = get_stock_price(stock_list, start_date_cal, end_date_cal) # 用于计算的数据
stock_price_test = get_stock_price(stock_list, start_date_test, end_date_test) # 用于测试的数据

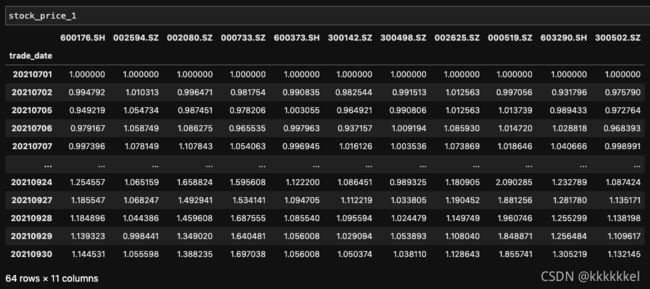
# 各股票净值从1开始，可以更直观地看出区别
stock_price_1 = dfUnification(stock_price) # 用于计算的数据
stock_price_1_test = dfUnification(stock_price_test) # 用于测试的数据

# 计算各股票的日收益率
stock_daily_returns = getDailyReturns(stock_price)
stock_daily_returns_test = getDailyReturns(stock_price_test)

# 计算相关矩阵
correlation_matrix = stock_daily_returns.corr()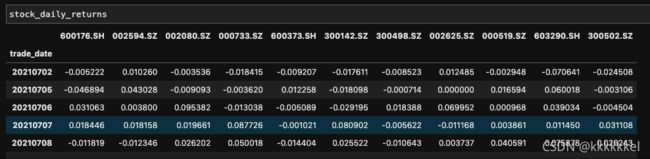

 股票在计算时间段的走势情况如下（初始净值为1，能够更好看清楚走势）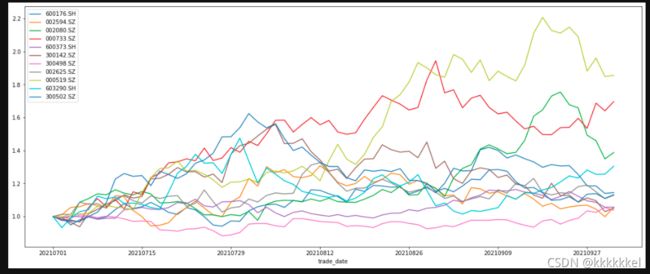

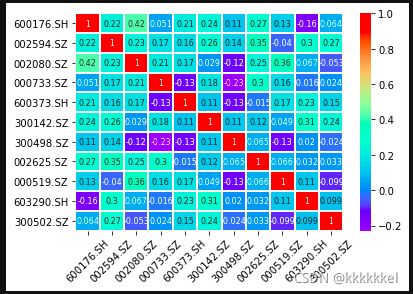
# 股票间相关系数热力图
sns.heatmap(correlation_matrix,annot=True,cmap='rainbow',linewidths=1.0,annot_kws={'size':8})
plt.xticks(rotation=45)
plt.yticks(rotation=0)
plt.show()

②用蒙特卡洛方法计算组合权重

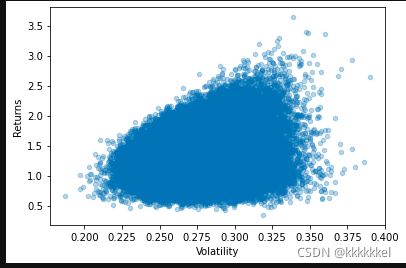
        这里计算的Returns是用日均收益率复合成年化的收益率。

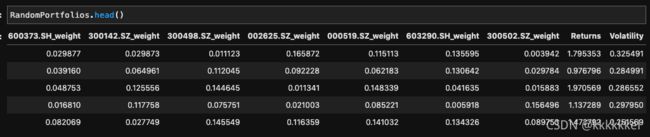
RandomPortfolios = monteCarloTest(stock_daily_returns)

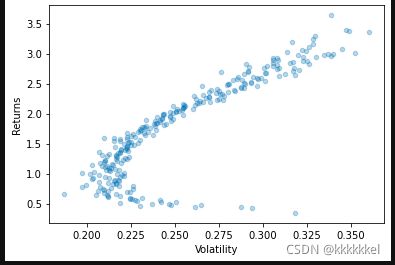
#绘制散点图
RandomPortfolios.plot('Volatility','Returns',kind='scatter',alpha=0.3)
plt.show()

 

③把有效前沿组合选出来

        由于Returns的小数位有点多，如果把小数位变少，那么在Returns值相等的情况下，再纵向选取最小的Volatility，就相当于把有效前沿的组合选出来了 。

RandomPortfolios['ReturnsRound'] = round(RandomPortfolios.Returns, 2)
returns_range = pd.DataFrame(sorted(RandomPortfolios['ReturnsRound'])).drop_duplicates()[0].tolist()
vol_min_idx_l = []
for i in returns_range:
    vol_min = RandomPortfolios[RandomPortfolios['ReturnsRound']==i].Volatility.min()
    vol_min_idx = RandomPortfolios[RandomPortfolios['Volatility']==vol_min].index[0]
    vol_min_idx_l.append(vol_min_idx)

RandomPortfolios.loc[vol_min_idx_l].plot('Volatility','Returns',kind='scatter',alpha=0.3)
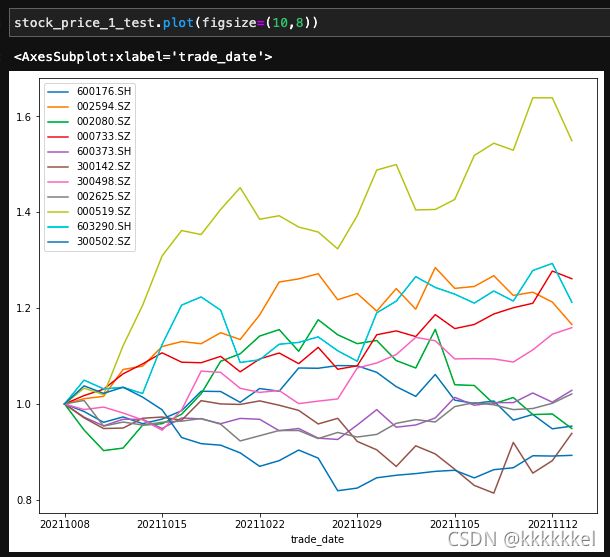
plt.show()

④测试时间段股票表现情况

        有个别股票跌得可以的。

 ⑤有效前沿组合在测试时间段的收益情况

        测试时间段的收益率用Returns_test表示，注意它不是年化收益率。

# 计算随机权重在测试时间段的收益率
Returns_test = []
for i in range(RandomPortfolios.shape[0]):
    Returns_test.append(stock_price_1_test.mul(\
                        np.array(RandomPortfolios.iloc[i,:stock_price_1_test.shape[1]]), axis=1).sum(axis=1).iloc[-1] - 1)

RandomPortfolios['Returns_test'] = Returns_test

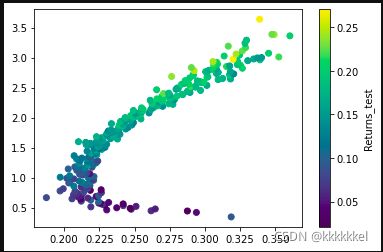
plt.scatter(RandomPortfolios.loc[vol_min_idx_l].Volatility, RandomPortfolios.loc[vol_min_idx_l].Returns, c=RandomPortfolios.loc[vol_min_idx_l].Returns_test)
plt.colorbar(label='Returns_test')
plt.show()

         有效前沿组合在测试时间段的收益还是可以的，并且基本遵循着风险与收益正比的关系。

四、思考

        本例中的结果是个例还是普遍存在，此策略能否复制？与选取的计算和测试的时间段是否有关系？若选取其他时间段是否也会有一致的结果？与选取的股票及组合中股票的数量是否也有关系？

        问题留给自己，也留给大家。

如果想要自定义的程序，请私信，谢谢！