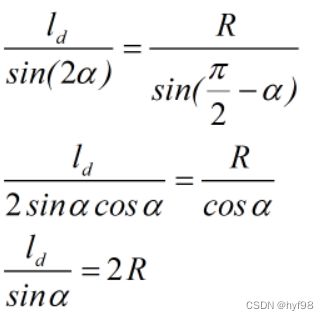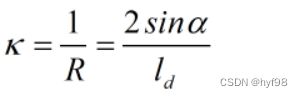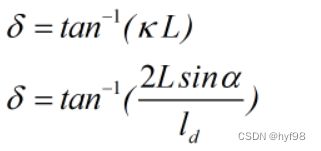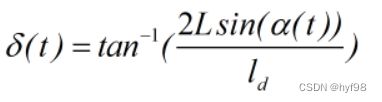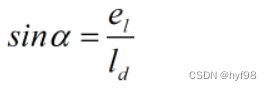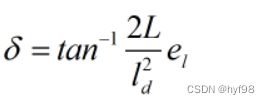园区自动驾驶实车平台决策规划控制系统（一）——基于纯追踪算法的横向控制（C++实现）

总结一下自己这一年的项目经验，由于本人技术水平有限，写作内容难免有错，如果发现还请不吝赐教~

在项目中本人负责的是自动驾驶的决策规划控制算法部分，在研发过程中负责对接上层感知定位模块和下层线控系统，项目实现了在园区场景下的自动驾驶。实现的场景包括单障碍物换道避障，多障碍物换道避障，跟车行驶，停车等待行人等。

接下来准备把项目中用到的横向控制、纵向控制、换道轨迹规划和决策模型分别记录，并附上核心代码，本文是第一篇。先放几个测试场景的视频作为预告。

 

园区自动驾驶（一）——基于Pure Pursuit的横向控制

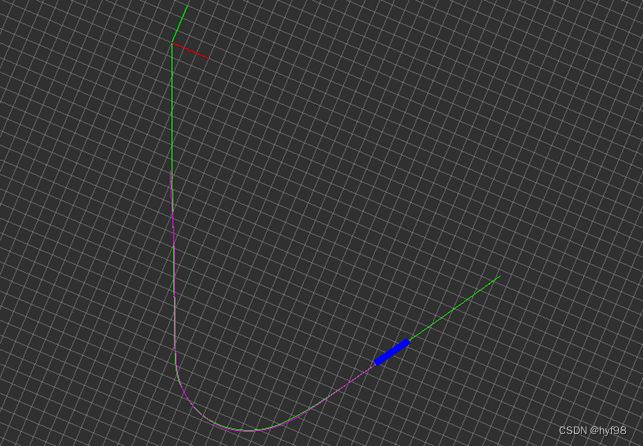
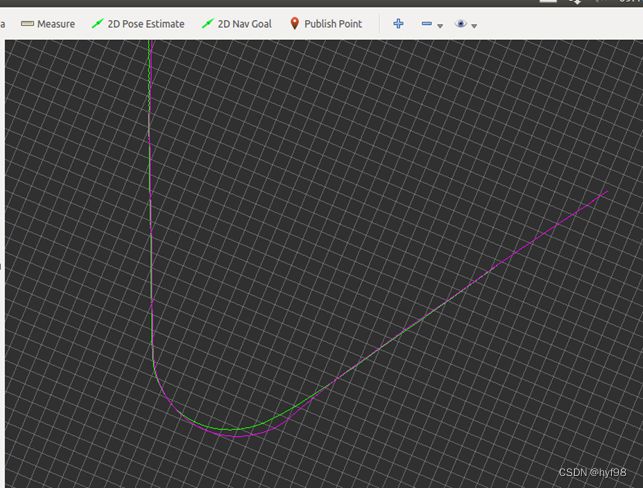
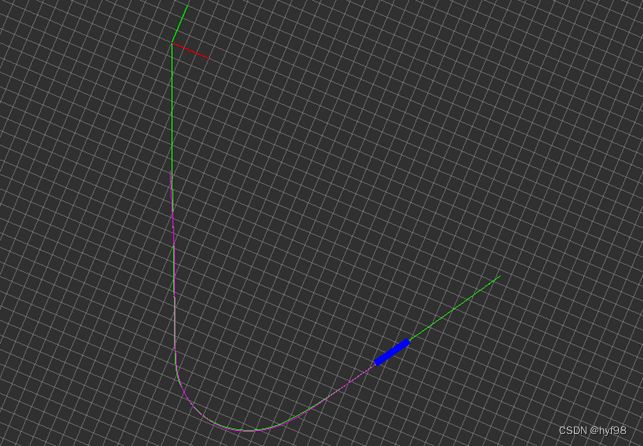
由于本文是针对园区的自动驾驶，车速较低，且循迹路径是一条固定的路线，测试路径如下图所示，图中：绿色路径是录制的离线路径，录制方法是手动开车时记录下组合惯导系统的实时定位，并保存；紫色的路径是实际行驶路径；蓝色长条不是车辆模型，长度也不是车身长度，蓝条后端是车辆当前位置（后轴），蓝条前端是纯追踪算法当前的目标点。

在讲纯追踪算法之前，先陈述下使用纯追踪算法对车辆运动学和动力学模型的简化。

车辆运动学和动力学模型简化

无人驾驶-控制-自行车模型_0->oo的博客-CSDN博客

二自由度车辆运动学模型和动力学模型这位大佬讲的很清楚，总结一下结论，简化包括：

• 不考虑车辆在Z轴方向的运动，只考虑XY水平面的运动，如下图所示；

• 左右侧车轮转角一致，这样可将左右侧轮胎合并为一个轮胎，以便于搭建单车模型，如图2所示；

• 车辆行驶速度变化缓慢，忽略前后轴载荷的转移；

• 车身及悬架系统是刚性的；

• 

简化结论有 ：

1、一般条件下：，其中 航向角为yaw，横摆角为；

但低速条件下，认为车不会发生侧向滑动（漂移），因此质心侧偏角 β ≈ 0，可得： 航向角yaw=横摆角 。

2、一般条件下，轮胎由于是胶体，会在压力下发生形变，导致轮胎侧偏；

但低速条件下，将轮胎视为完全刚体，不会发生变形，不考虑轮胎侧偏，且后轮一般不转向，因此后轮转角  。

bicycle模型

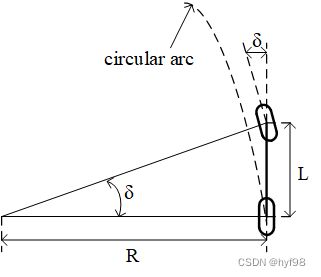
在以上简化假设都成立的情况下，才能将四轮akerman转向模型简化为二轮bicycle模型。

 

如上图所示，bicycle模型中，L是车的轴距，R是当前转向角下，车辆遵循的转弯半径，可以得到前轮转角δ 为：

        

纯追踪算法推导

接下来就是老生常谈的推导了，图懒得用visio画了，手画快些。

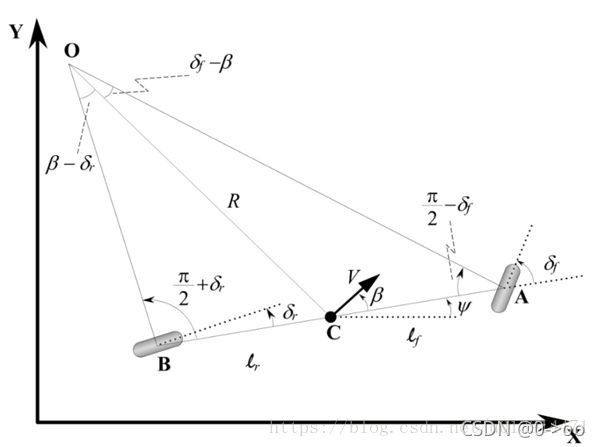
 将四轮akerman模型简化成bicycle模型后，从录制的离线路径中选取下一个要追踪的目标点G(gx,gy)，控制目标是让车辆的后轴中点S（组合惯导系统位于车辆后轴，因此定位得到的车辆当前位置其实是车辆后轴的位置）经过该目标点G。

目标点G，车辆位置S和转向圆圆心三个点构成了一个等腰三角形，根据正弦定理，可以推出以下三个公式：

其中R为转向圆半径；  是希望控制车辆到达的下一个位置，即 look-ahead distance（前视距离）：人类驾驶员开车时，眼睛看向道路前方的位置就是想开到的地方；纯追踪算法也一样，变成了在离线轨迹上寻找下一个期望到达的位置；夹角 α 为车身坐标系的x轴与车身坐标系原点与目标点的夹角，夹角 α 如下图所示。

1/R也就是这段圆弧的曲率，为：

 

 将1/R带入到bicycle模型的前轮转角公式中，可得：

将转角 δ 视作时间 t 的函数，可得：

 上式就是纯跟踪算法的输出表达式，输出量为车辆前轮转角 δ 。

为了更好的理解影响纯跟踪算法精度的因素，定义车辆当前位姿 S 和目标点 G 的横向误差 ，可得夹角 α 正弦：

 转角 δ 可以重写为：

 由于轴距 L 是常数，横向误差  是自变量，因此因变量 δ 的控制效果主要取决于前视距离 。

通常来说， 被认为是车速的函数，需要根据车速传感器反馈的当前车速来实时更新当前的前视距离。

除了车速外，道路曲率也是影响循迹精度的关键。在弯道下，前视距离如果太大，可能导致循迹精度下降。

因此，本文将前视距离视作是车速和道路曲率的一次函数，即 ，那么前轮的转角公式就变为：

其中， 为最小前视距离，本文的最小前视距离大小根据道路曲率设置：如果道路曲率太大，则减小  ，使追踪更加精确；如果道路曲率较小，则增大   ，使轨迹追踪更平滑。

 基于C++的纯追踪算法实车实现核心代码

 本实现方法在ros环境下实现，纯追踪算法只用来控制转向角度，速度控制将在下一篇纵向控制中介绍。

首先根据实车型号定义各项参数。

#define  K          (1.5)       // 前视距离系数
#define  L_VEHICLE  (2.9)       // 车的轴距
int L0 = 1;    //最小前视距离，根据道路曲率变化   

本文将最小前视距离设为1 m，前视距离系数设为1.5 ，AionLX 车的轴距为2.9m。

定义车辆状态类，在bicycle模型中，位姿只考虑车辆当前世界坐标系下坐标（x，y）,车辆偏航角yaw，以及车辆的速度speed：

struct State{
  double x = 0;          // m
  double y = 0;          // m
  double yaw = 0;        // degree
  double speed = 0;      // m/s
};
State vehicleState;

订阅话题，接受定位和传感器节点发布的消息，更新车辆状态：

        vehicle_location = node.subscribe("/geometry_pose", 2, &pure_pursuit::location_update, (pure_pursuit *) this);
        veh_speed = node.subscribe("/vehicle_response", 2, &pure_pursuit::vehReportCallback,  (pure_pursuit *) this);

接收定位传来的当前位姿，包括世界坐标系坐标和四元数，用ros的tf::Quaternion库将四元数转为 roll，pitch 和 yaw，得到航向角yaw：

//用PoseStamped更新位姿(x,y,yaw)
    void pure_pursuit::location_update(const geometry_msgs::PoseStamped::ConstPtr locat) {
        vehicleState.x = locat->pose.position.x;
        vehicleState.y = locat->pose.position.y;

        //根据当前位置更新最小前视距离L0，其中boundary是直道和弯道的分界点
        if(vehicleState.x>boundary.x&&vehicleState.y>boundary.y){
            L0=1;   //最小前视距离默认为2，弯道上变为1
        }

        //用vehLocUpdatRdy表示位姿是否更新，默认为false
        vehLocUpdatRdy = true;

        tf::Quaternion quat(locat->pose.orientation.x, locat->pose.orientation.y, locat->pose.orientation.z, locat->pose.orientation.w);

        // 用tf::Quaternion库将四元数转为 roll pitch 和 yaw
        double roll, pitch, yaw;
        tf::Matrix3x3(quat).getRPY(roll, pitch, yaw);

        vehicleState.yaw = yaw;
    }

 接受传感器传来的当前车速，更新当前车速：

//用传感器回调函数更新当前车速
void pure_pursuit::vehReportCallback(const common_msgs::veh_response::ConstPtr &veh_report_msg)
    {
        vehicleState.speed = static_cast(veh_report_msg->veh_spd);
    }

 纯追踪横向控制核心代码：

//根据目标进行转角控制
    double pure_pursuit::pure_pursuit_control(const State &s, const vector  &path, int *lastIndex) {
        int index = get_goal_index(s, path); // 搜索目标点，返回目标点的标签

        // 用上一个循环的目标点判断是否是在向前走
        if (index <= *lastIndex) {
            index = *lastIndex;
        }

        Point goal;

        //防止index溢出
        if (index < path.size()) {
            goal = path[index]; 
        } else {
            index = path.size() - 1;
            goal = path[index];
        }

        // 车身坐标系的x轴和目标点与车身坐标系原点连线的夹角
        double alpha = atan2(goal.y - s.y, goal.x - s.x) - s.yaw;

        if (s.speed < 0)
            alpha = M_PI - alpha;

        double lf = K * s.speed + L0; // 根据车速和道路曲率设置前视距离
        // delta 即为纯跟踪算法的最终输出
        double delta = atan2((2.0 * L_VEHICLE * sin(alpha)) / lf, 1.0);

        *lastIndex = index;      // 为下一个循环更新上一个目标点
        return delta;
    }

 定义函数用于搜索最近的目标点：

//index为跟踪目标
    int pure_pursuit::get_goal_index(const State &s, const vector  &path) {
        vector d;
        for (int i = 0; i < path.size(); i++)
            d.push_back(pow((s.x - path[i].x), 2) + pow((s.y - path[i].y), 2));//距离计算

        int index = 0;
        double d_min = d[0];
        int dVecLen = d.size();

        //找到距离车辆最近的路径点
        for (int i = 0; i < dVecLen; i++) {
            if (d_min > d[i]) {
                d_min = d[i];
                index = i;
            }
        }

        double l = 0;
        double lf = K * s.speed + L0;
        double dx_, dy_;

        //积分法计算路径长度
        while (l < lf && index < path.size()) {
            dx_ = path[index + 1].x - path[index].x;
            dy_ = path[index + 1].y - path[index].y;
            l += sqrt(dx_ * dx_ + dy_ * dy_);
            index++;
        }

        return index;
    }

发送转角给线控系统执行：

    bool pure_pursuit::track_follow_process(const vector  &pathVet) {
        bool isjobDone = false;
        
        //判断路径是否走完
        if (goalIndex < rearIndex) {

            //获取纯跟踪输出的前轮转角
            delta = pure_pursuit_control(vehicleState, pathVet, &goalIndex);

            wheelAngle = delta * 180 / M_PI;
            wheelAngle = -1 * wheelAngle;  //前轮转角为弧度制，逆时针为正，AionLX车的顺时针转向为正，逆时针为负，刚好相反

            //AionLX前轮转角最大为40°
            if (wheelAngle > 40.0) wheelAngle = 40.0;
            if (wheelAngle < -40.0) wheelAngle = -40.0;

        }
        
        //如果走完，则急停
        if (goalIndex >= rearIndex)
            isjobDone = true;
        
        //发布前轮转角
        std_msgs::Float32 tempAngleSet;
        tempAngleSet.data = wheelAngle;
        strAngle_pub.publish(tempAngleSet);

        return isjobDone;
    }

 以上就是纯追踪算法的核心代码，经实车实验，平均误差小于10cm。如下左图，由于设置的最大前轮转角不够大，且前视距离设置较大，所以在急剧转角处出现了转向不足的情况；将最大前轮转角改为40°，前视距离改小后，如下右图，在大弯道也能准确循迹。

 

小结

 纯追踪算法是一种几何路径跟踪算法，很适合新手上手使用。优点是很大地简化了车辆运动学和动力学模型，输入输出明确，在低速下能获得较好地控制效果；缺点是简化了太多的车辆运动学和动力学模型，所以只要速度和加速度提高，运动学动力学简化条件不再成立，就无法保证横向控制精度。

 本项目由于是在园区内行驶，车速不会高于10km/h，所以纯追踪算法能够达到横向控制需求。但目前选择最佳前视距离的方法并不一定，本文将  视作纵向速度和路径曲率相关的一次函数，大的前视距离可以使控制更平滑，但在大转角处会转向不足；前视距离太小又会带来控制的震荡(前轮转角变动幅度很大)。 因此，影响横向控制精度地前视距离  的选取仍有待优化。

参考博客

无人驾驶汽车系统入门（十八）——使用pure pursuit实现无人车轨迹追踪_AdamShan的博客-CSDN博客自动驾驶（七十一）---------Pure Pursuit轨迹追踪_一实相印的博客-CSDN博客_自动驾驶轨迹跟踪

无人驾驶-控制-阿克曼模型_0->oo的博客-CSDN博客_阿克曼模型