Java | 基础算法 - 排序：冒泡排序 代码实现（含详细注释）

冒泡排序(BubbleSort)

一、基本思想

将待排序的数组看成从上到下排放，把关键字值较小的记录看成“较轻的”，关键字值比较大的记录看成“较重的”，较小关键字值的记录好像水中的气泡一样，向上浮；较大关键字值的记录如水中的石块向下沉，当所有的气泡都浮到了相应的位置，并且所有的石块都沉到了水中，排序就结束了。

二、原理图解

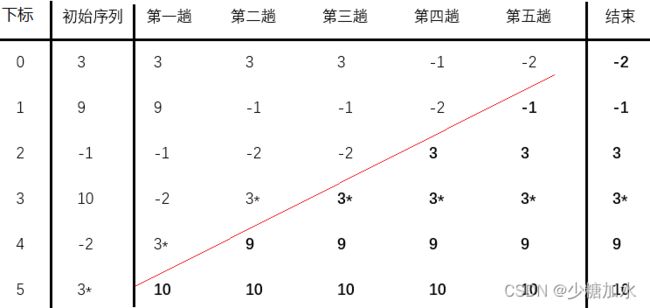
假设待排序的6个记录的关键字序列为{3，9，-1，10，-2，3*}，图解如下——

【注：带星号的关键字值相同，在此只是为了区分两个相同关键字值。】

第一趟：将前后数据元素进行对比，10是最大的，所以把10交换到最底下；

第二趟：排除掉{10}，将剩下的数据元素继续前后对比，9是最大的，所以把9沉到次底下；

......

第五（n-1）趟：排除掉{-1,3,3*，9,10}，只剩下-2，无需交换。

结束：得到有序序列{-2，-1,3,3*，9,10}。

三、算法步骤

假设记录存放在数组r中，开始时，有序序列为空，无序序列为{r[0],r[1],...,r[n-1]}，则将冒泡排序算法的主要步骤归纳如下：

1）置初值1；

2）在无序序列{r[0],r[1],...,r[n-1]}中，从头至尾一次比较相邻的两个记录r[j]与r[j+1]（0<=j<=n-i-1）,若r[j].key>r[j+1].key，则交换位置。

3）i = i + 1。

4）重复步骤 2）和 3），直到步骤 2) 中 未发生记录交换或 i = n-1 为止。

大家看前面这段文字可能会觉得枯燥，难以理解，所以下面我再用自己的话通俗易懂地讲述一下代码实现的步骤：

使用双重循环——

内循环是为了遍历序列中每一个数据元素，通过前后对比，将最大的数据元素沉到最底下；

由于每内循环一次，只能将一个最大的数据元素沉到最底下，因此必须进行n-1趟（也就是案例中的5趟）排序才能够将所有的数据元素都沉到底下。

//优化

而这里还有一个局限性，就是外循环的次数其实并不一定需要进行n-1趟，举个栗子：如果待排序序列是局部有序的-{6,84,20,1,2,3,4}，那么循环到第四趟的时候，就已经得到有序序列，如果继续循环，那将是没有意义的。

所以我们在这里再引入一个布尔变量flag，用来标记当前这一趟内循环有没有发生交换，如果没有，直接结束循环就可以得到最终序列。

四、代码实现

import java.util.Arrays;

public class BubbleSort {
	public static void main(String[] args) {
		int arr[] = {3,9,-1,10,-2,3};
		System.out.println("排序前的数组：" + Arrays.toString(arr));
		//测试冒泡排序
		bubbleSort(arr);
		System.out.println("排序后的数组：" + Arrays.toString(arr));
	}
	
	public static void bubbleSort(int[] arr) {
		int temp = 0;  //临时变量
		boolean flag = false;  //标识变量，表示是否进行过交换
		for(int i = 0;i < arr.length - 1;i++) {
			for(int j = 0;j < arr.length - 1 - i;j++) {
				//如果前面的数比后面的数大，则交换
				if(arr[j] > arr[j + 1]) {
					flag = true;
					temp = arr[j];
					arr[j] = arr[j + 1];
					arr[j + 1] = temp;
				}
			}	
			//打印每趟排序的结果
			System.out.println("第" + (i + 1) + "趟排序后的数组：");
			System.out.println(Arrays.toString(arr));
			if(flag == false) {
				break;
			}else {
				flag = false;  //重置flag，进行下次判断
			}
		}
	}
}

五、算法性能分析

1）空间复杂度。O(1)

2）时间复杂度。O(n2)

3）算法稳定性。

冒泡排序是一种稳定的排序算法。【案例中3和3*前后顺序保持不变】