[LeetCode周赛复盘] 第 299 场周赛20220626

@TOC

一、本周周赛总结

再次感觉到自己的菜。
最后一题图论，是真的不会，打死都不会。
赛后看大佬讲解，照着大佬代码复写，大概理解了，但是再给我一道新题，估计还是做不出来。
得练。

二、 [Easy] 6101. 判断矩阵是否是一个 X 矩阵

链接: 6101. 判断矩阵是否是一个 X 矩阵

1. 题目描述

判断矩阵是否是一个 X 矩阵

难度：简单

如果一个正方形矩阵满足下述全部条件，则称之为一个 X 矩阵 ：

矩阵对角线上的所有元素都 不是 0
矩阵中所有其他元素都是 0

给你一个大小为 n x n 的二维整数数组 grid ，表示一个正方形矩阵。如果 grid 是一个 X 矩阵 ，返回 true ；否则，返回 false 。

示例 1：

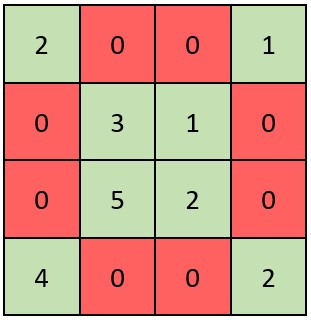
输入：grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
输出：true
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 是一个 X 矩阵。

示例 2：

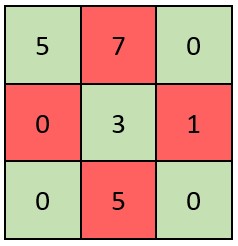
输入：grid = [[5,7,0],[0,3,1],[0,5,0]]
输出：false
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 不是一个 X 矩阵。

提示：

n == grid.length == grid[i].length
3 <= n <= 100
0 <= gridi <= 10⁵

2. 思路分析

定级Easy。
按题意模拟即可。

3. 代码实现

class Solution:
    def checkXMatrix(self, grid: List[List[int]]) -> bool:
        m,n = len(grid),len(grid[0])
        for i in range(m):
            for j in range(n):
                if i == j and grid[i][j] == 0:
                    return False
                if i+j == m-1 and grid[i][j] == 0:
                    return False
                if not (i==j or i+j==m-1) and grid[i][j] != 0:
                    return False
        
        return True

三、[Medium] 6100. 统计放置房子的方式数

链接: 6100. 统计放置房子的方式数

1. 题目描述

统计放置房子的方式数

难度：中等

一条街道上共有 n * 2 个地块，街道的两侧各有 n 个地块。每一边的地块都按从 1 到 n 编号。每个地块上都可以放置一所房子。

现要求街道同一侧不能存在两所房子相邻的情况，请你计算并返回放置房屋的方式数目。由于答案可能很大，需要对 10⁹ + 7 取余后再返回。

注意，如果一所房子放置在这条街某一侧上的第 i 个地块，不影响在另一侧的第 i 个地块放置房子。

示例 1：

输入：n = 1
输出：4
解释：
可能的放置方式：
1. 所有地块都不放置房子。
2. 一所房子放在街道的某一侧。
3. 一所房子放在街道的另一侧。
4. 放置两所房子，街道两侧各放置一所。

示例 2：

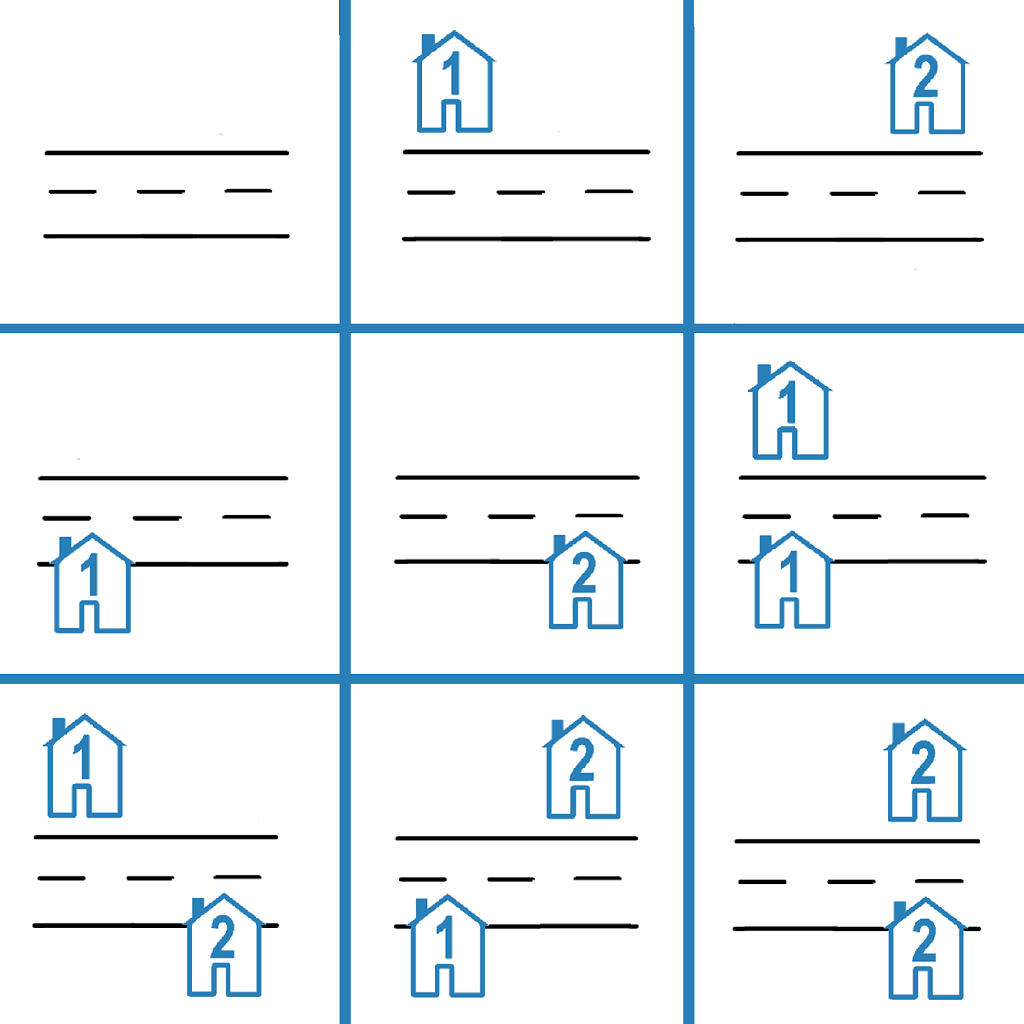
输入：n = 2
输出：9
解释：如上图所示，共有 9 种可能的放置方式。

提示：

1 <= n <= 10⁴

2. 思路分析

定级Medium。

实际是斐波那契数列，比赛时没看出来，写了记忆化搜索，反正也过了。
道路两边没有互相限制，而且两边情况实际相同，因此算一边，然后平方即可。
第0块地，只有1种方法，就是不放。
第i块地，如果自己放，只能从上块地不放的情况转移过来；如果自己不放，上块地可以放或不放。

3. 代码实现

class Solution:
    def countHousePlacements(self, n: int) -> int:
        mod = 10**9+7
        
        def q_pow(base, power):
            res = 1
            while power > 0:
                if power & 1 == 1:
                    res = res * base % mod
                power >>= 1
                base = base * base % mod
            return res % mod
        @cache
        def dfs(i,has):
            if i == 0:
                return 1
            ans = dfs(i-1,False)
            if not has:
                ans += dfs(i-1,True)
            return ans % mod
        ret = (dfs(n-1,False) + dfs(n-1,True)) %mod
        return ret*ret%mod

四、[Hard] 5229. 拼接数组的最大分数

链接: 5229. 拼接数组的最大分数

1. 题目描述

拼接数组的最大分数

难度：困难

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，长度都是 n 。

你可以选择两个整数 left 和 right ，其中 0 <= left <= right < n ，接着交换两个子数组 nums1[left...right] 和 nums2[left...right] 。

例如，设 nums1 = [1,2,3,4,5] 和 nums2 = [11,12,13,14,15] ，整数选择 left = 1 和 right = 2，那么 nums1 会变为 [1,12,13,4,5] 而 nums2 会变为 [11,2,3,14,15] 。

你可以选择执行上述操作一次或不执行任何操作。

数组的分数取 sum(nums1) 和 sum(nums2) 中的最大值，其中 sum(arr) 是数组 arr 中所有元素之和。

返回 可能的最大分数 。

子数组 是数组中连续的一个元素序列。arr[left...right] 表示子数组包含 nums 中下标 left 和 right 之间的元素（含下标 left 和 right 对应元素）。

示例 1：

输入：nums1 = [60,60,60], nums2 = [10,90,10]
输出：210
解释：选择 left = 1 和 right = 1 ，得到 nums1 = [60,90,60] 和 nums2 = [10,60,10] 。
分数为 max(sum(nums1), sum(nums2)) = max(210, 80) = 210 。

示例 2：

输入：nums1 = [20,40,20,70,30], nums2 = [50,20,50,40,20]
输出：220
解释：选择 left = 3 和 right = 4 ，得到 nums1 = [20,40,20,40,20] 和 nums2 = [50,20,50,70,30] 。
分数为 max(sum(nums1), sum(nums2)) = max(140, 220) = 220 。

示例 3：

输入：nums1 = [7,11,13], nums2 = [1,1,1]
输出：31
解释：选择不交换任何子数组。
分数为 max(sum(nums1), sum(nums2)) = max(31, 3) = 31 。

提示：

n == nums1.length == nums2.length
1 <= n <= 10⁵
1 <= nums1[i], nums2[i] <= 10⁴

2. 思路分析

定级Hard。
这题看起来唬人，实际可以转化成一个简单题。

我们假设目标是从nums1中找一段给nums2，使s2=nums2最大，设这一段为区间[l,r]。
那么s2将会变成s2-nums[l,r]+nums1[l,r]。即s2+diff[l,r],diff[i]=nums1[i]-nums2[i]
diff可以用 O(n) 处理出来，问题转化成，寻找diff中最大子串和。
这是一道简单的dp入门题，也是我的入坑题。
最后，我们分别讨论从nums1给nums2，和从num2给num1的情况，取max即可。
特殊的，这题可以不转化，那么加max(diff)的时候,负数置0.

3. 代码实现

class Solution:
    def maximumsSplicedArray(self, nums1: List[int], nums2: List[int]) -> int:
        n = len(nums1)
        
        def max_subarr(nums1,nums2):
            s2 = sum(nums2)
            diff = [nums1[i]-nums2[i] for i in range(n)]
            
            for i in range(1,n):
                if diff[i-1] >0 :
                    diff[i] += diff[i-1]
            return s2 + max(0,max(diff))
        return max(max_subarr(nums1,nums2),max_subarr(nums2,nums1))

五、[Hard] 6103. 从树中删除边的最小分数

链接: 6103. 从树中删除边的最小分数

1. 题目描述

从树中删除边的最小分数

难度：困难

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点，以及 n - 1 条边。

给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [a_i, b_i] 表示树中存在一条位于节点 a_i 和 b_i 之间的边。

删除树中两条不同的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

分别获取三个组件每个组件中所有节点值的异或值。
最大异或值和最小异或值的差值就是这一种删除边方案的分数。

例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ，最小异或值是 3 ，分数是 8 - 3 = 5 。

返回在给定树上执行任意删除边方案可能的最小分数。

示例 1：

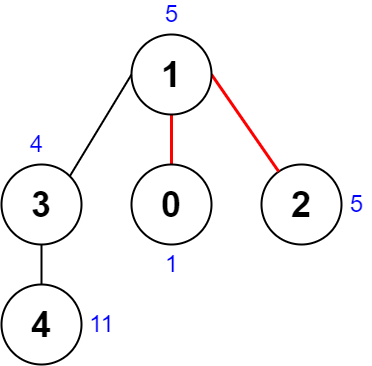
输入：nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出：9
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [1,3,4] ，值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
- 第 2 个组件的节点是 [0] ，值是 [1] 。异或值是 1 = 1 。
- 第 3 个组件的节点是 [2] ，值是 [5] 。异或值是 5 = 5 。
分数是最大异或值和最小异或值的差值，10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。

示例 2：

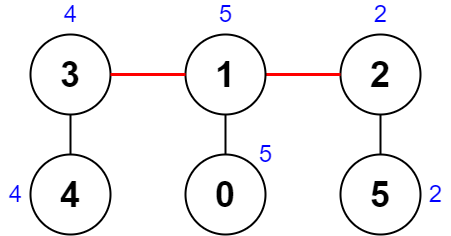
输入：nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出：0
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [3,4] ，值是 [4,4] 。异或值是 4 ^ 4 = 0 。
- 第 2 个组件的节点是 [1,0] ，值是 [5,5] 。异或值是 5 ^ 5 = 0 。
- 第 3 个组件的节点是 [2,5] ，值是 [2,2] 。异或值是 2 ^ 2 = 0 。
分数是最大异或值和最小异或值的差值，0 - 0 = 0 。
无法获得比 0 更小的分数 0 。

提示：

n == nums.length
3 <= n <= 1000
1 <= nums[i] <= 10⁸
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
edges 表示一棵有效的树

2. 思路分析

定级Hard。
这题真的难啊！
不会做啊！
题解都看不懂啊！
最后照着大佬代码复写硬啃才过的。

由于异或的性质，我们无法剪枝，即：枚举两条边，只能用 O(n^2)来做，且列举所有删除后，三部分的异或和来更新答案。
题目数据范围是1000，枚举已经n^2了，因此我们需要一个O(1)的方法计算删除两条边后，三部分的异或和。
比赛时我有用的并查集，总体复杂度是O(n^3)，不出意料TLE了，不过确实不会做，就这么交了也没办法，交着玩呗。
正确做法：
- 随便选一个节点作为根节点(这里选0)，把这无向图预处理成树，然后预处理每个子树的异或和，记在子树的根上。
- 那么删除两条边后，三部分的异或和都可以通过O(1)计算出来了。
- 这2条边i,j分别讨论三种情况：
  1) i是j的长辈。
  2) j是i的长辈.
  3) i,j没有长辈关系。
  4) 参考以下摘录@灵茶山艾府大佬的图。
  5) 这三种情况下，三部分的异或和都是可以O(1)计算出来的。
- 那么如何预处理子树异或和以及判断长辈关系呢。
- dfs处理子树异或和，这个比较简单。
- 长辈关系，涉及到一个时间戳的概念，定义一个全局的计数器，其实就是先根遍历时，节点的访问顺序，用这个时间戳来记录：
  每个节点的进入时间in和退出时间out。
- 那么如果u是v的长辈，则有 _in[u] <= _in[v] <= _out[u]，反之亦然，可以用这个判断。
- 最后还要调整一下边中，给出u，v的顺序，让长辈在前边，等于给边方向，这样好写。

3. 代码实现

class Solution:
    def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int:
        n,m = len(nums),len(edges)
        graph = defaultdict(list)
        for u,v in edges:
            graph[u].append(v)
            graph[v].append(u)
        
        clock = 0
        xor = [0] * n  # 以i为根的子树异或和
        _in = [0] * n
        _out = [0] * n
        # 返回以u为根的子树异或和，查询时，father是u的父亲节点。
        # 同时计算u的出入时间戳
        def dfs(u, father):
            nonlocal clock
            clock += 1
            _in[u] = clock
            xor[u] = nums[u]
            for v in graph[u]:
                if v != father:
                    xor[u] ^= dfs(v,u)
            _out[u] = clock
            return xor[u]
        
        dfs(0,-1)
        # u是v的长辈节点
        def is_parent(u,v):
            return _in[u] <= _in[v] <= _out[u]
        
        # 对每条边给出节点的前后进行调整，让长辈在前边
        # 等于给边方向
        for e in edges:
            if not is_parent(e[0],e[1]):
                e[0],e[1] = e[1],e[0]

        ans = inf
      
        for (u1,v1),(u2,v2) in  combinations(edges,2):
            if is_parent(v2,u1):  # j边是i边的长辈，从下往上的三部分子树异或和分别为v1,v2-v1,根-v2
                a,b,c = xor[v1],xor[v2]^xor[v1],xor[0]^xor[v2]
            elif is_parent(v1,u2):  # i边是j边的长辈，从下往上的三部分子树异或和分别为v1,v1-v2,根-v1
                a,b,c = xor[v2],xor[v1]^xor[v2],xor[0]^xor[v1]
            else:  # i,j没有长辈关系(分属子树),三部分分别为v1,v2,根-v1-v2
                a,b,c = xor[v1],xor[v2],xor[0]^xor[v1]^xor[v2]
            ans = min(ans,max(a,b,c)-min(a,b,c))
            if ans == 0:
                return 0

        return ans

六、参考链接

灵神的题解：DFS 时间戳——处理树上问题的有力工具（Python/Java/C++/Go）

人生苦短，我用Python！

[LeetCode周赛复盘] 第 299 场周赛20220626

一、本周周赛总结

二、 [Easy] 6101. 判断矩阵是否是一个 X 矩阵

1. 题目描述

2. 思路分析

3. 代码实现

三、[Medium] 6100. 统计放置房子的方式数

1. 题目描述

2. 思路分析

3. 代码实现

四、[Hard] 5229. 拼接数组的最大分数

1. 题目描述

2. 思路分析

3. 代码实现

五、[Hard] 6103. 从树中删除边的最小分数

1. 题目描述

2. 思路分析

3. 代码实现

六、参考链接

你可能感兴趣的:(python)