神经网络算法识别手写数字minst
神经网络算法识别手写数字minst
- 神经网络算法概述
-
- 神经元模型
- 多层前馈神经网络
- backpropagation算法(BP算法)
- 识别手写数字
-
- minst数据集介绍
- 编码流程
- 完整代码
神经网络算法概述
神经元模型
- x 1 x_1 x1到 x n x_n xn表示输入的特征,在实际的编码当中会转化成向量或是矩阵来操作。
- w i n w_{in} win表示第一层的权重,其中i表示层数,n表示特征的个数。
- w i 0 w_{i0} wi0表示偏置量, x 0 x_0 x0一般设置为1或是-1,这样就可以将偏置量直接包含到矩阵乘法运算当中,不需要额外去做加减运算。
- f f f为激活函数,一般可以选择sigmoid函数或是ReLU函数。
- 激活函数的作用:如果不使用激活函数,那么经过一层神经网络得到的都是输入的特征的线性组合,这样的结果是没有意义的。
- 偏置量的作用:可以先想象只有一个输入,一个权重的情况下,那么这时候就是做一条过原点的直线对输入数据进行分类;或者说三维的情况下就是一个过原点的平面。所以不包含偏置量的话,模型的分类能力会很差。
多层前馈神经网络

以一个两层神经网络(输入层一般不计算在内,又称为单隐层神经网络)为例,每一层的计算过程比较像逻辑回归。
- 输入层第i个单元的输入为: x i x_i xi
- 隐藏层第h个单元的输入: α h = ∑ i = 1 d v i h x i \alpha_h = \sum_{i=1}^{d} v_{ih} x_i αh=∑i=1dvihxi
- 隐藏层第h个单元的输出:需要考虑偏置以及激活函数
b h = S i g m o i d ( α h − θ h ) b_h = Sigmoid(\alpha_h-\theta_h) bh=Sigmoid(αh−θh) - 输出层第j个单元的输入: β j = ∑ h = 1 q v h j b h \beta_j = \sum_{h=1}^{q} v_{hj} b_h βj=∑h=1qvhjbh
- 输出层第j个单元的输出:需要考虑偏置以及激活函数
y ^ j = S i g m o i d ( β j − θ j ) \hat y_j = Sigmoid(\beta_j-\theta_j) y^j=Sigmoid(βj−θj)
backpropagation算法(BP算法)
根据链式求导法则对前面的权值进行更新,与逻辑回归当中也有相似之处,同时,由于偏置量是通过 x 0 x_0 x0整合到了权值当中,所以在更新权值的同时,偏置量也会同时更新。本部分具体可以看西瓜书中的推导。


识别手写数字
minst数据集介绍
- 第1-4个byte (字节, 1byte=8bit),即前32bit存的是文件的magic number,对应的十进制大小是2051,2051则表示文件存储的是图片。
- 第5-8个byte存的是number of images,即图像数量60000;
- 第9-12个byte存的是每张图片行数/高度,即28;
- 第13-16个byte存的是每张图片的列数/宽度,即28。
- 从第17个byte开始,每个byte存储一张图片中的一个像素点的值。从前面可以得知,每一张图片都是28*28,所以存储一张图片需要784bytes空间。
- 本身minst官网中的数据已经是划分好了训练集以及测试集,训练集包含60000数据,测试集包含10000数据。
- 下图是将存储的 像素值还原为图片之后的样子

编码流程
- 参数的初始化
在构造函数当中,需要指定输入层、隐藏层以及输出层的节点数量,要指定一个初始的学习率,随机初始化两层之间连接上的权值,指定激活函数为sigmoid函数(可以直接使用科学计算库当中的库函数)。
def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
self.inputNodes = inputnodes
self.hiddenNodes = hiddennodes
self.outputNodes = outputnodes
self.lr = learningrate
self.wih = numpy.random.normal(0.0, pow(self.hiddenNodes, -0.5), (self.hiddenNodes, self.inputNodes))
self.vho = numpy.random.normal(0.0, pow(self.outputNodes, -0.5), (self.outputNodes, self.hiddenNodes))
self.activationFunction = lambda x: scipy.special.expit(x)
- 参数更新
根据BP算法得出的公式对参数进行更新。
def train(self, inputLists, targetList):
inputs = numpy.array(inputLists, ndmin=2).T
targets = numpy.array(targetList, ndmin=2).T
hiddenInputs = numpy.dot(self.wih, inputs)
hiddenOutputs = self.activationFunction(hiddenInputs)
finalInputs = numpy.dot(self.vho, hiddenOutputs)
finalOutputs = self.activationFunction(finalInputs)
outputErrors = targets - finalOutputs
hiddenErrors = numpy.dot(self.vho.T, outputErrors)
#对vho进行更新
self.vho += self.lr * numpy.dot((outputErrors * finalOutputs * (1.0 - finalOutputs)),
numpy.transpose(hiddenOutputs))
self.wih += self.lr * numpy.dot((hiddenErrors * hiddenOutputs * (1.0 - hiddenOutputs)),
numpy.transpose(inputs))
- 前向传播
def predict(self, inputLists):
inputs = numpy.array(inputLists, ndmin=2).T
hiddenInputs = numpy.dot(self.wih, inputs)
hiddenOutputs = self.activationFunction(hiddenInputs)
finalInputs = numpy.dot(self.vho, hiddenOutputs)
finalOutputs = self.activationFunction(finalInputs)
return finalOutputs
- minst数据集处理,需要将每个像素进行归一化, 都变换到0-1之间再进行处理。
- 可以使用sklearn中提供的方法方便的求出混淆矩阵。
完整代码
神经网络类
import numpy
import scipy.special
import matplotlib.pyplot
numpy.set_printoptions(suppress=True)
class neuralNetwork:
def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
self.inputNodes = inputnodes
self.hiddenNodes = hiddennodes
self.outputNodes = outputnodes
self.lr = learningrate
self.wih = numpy.random.normal(0.0, pow(self.hiddenNodes, -0.5), (self.hiddenNodes, self.inputNodes))
self.vho = numpy.random.normal(0.0, pow(self.outputNodes, -0.5), (self.outputNodes, self.hiddenNodes))
self.activationFunction = lambda x: scipy.special.expit(x)
def train(self, inputLists, targetList):
inputs = numpy.array(inputLists, ndmin=2).T
targets = numpy.array(targetList, ndmin=2).T
hiddenInputs = numpy.dot(self.wih, inputs)
hiddenOutputs = self.activationFunction(hiddenInputs)
finalInputs = numpy.dot(self.vho, hiddenOutputs)
finalOutputs = self.activationFunction(finalInputs)
outputErrors = targets - finalOutputs
hiddenErrors = numpy.dot(self.vho.T, outputErrors)
#对vho进行更新
self.vho += self.lr * numpy.dot((outputErrors * finalOutputs * (1.0 - finalOutputs)),
numpy.transpose(hiddenOutputs))
self.wih += self.lr * numpy.dot((hiddenErrors * hiddenOutputs * (1.0 - hiddenOutputs)),
numpy.transpose(inputs))
def predict(self, inputLists):
inputs = numpy.array(inputLists, ndmin=2).T
hiddenInputs = numpy.dot(self.wih, inputs)
hiddenOutputs = self.activationFunction(hiddenInputs)
finalInputs = numpy.dot(self.vho, hiddenOutputs)
finalOutputs = self.activationFunction(finalInputs)
return finalOutputs
处理minst数据集并对手写数字进行训练、识别。
import csv
inputNodes = 784 #输入层节点数量 28*28
hiddenNodes = 100 #隐藏层节点数量
outputNodes = 10 #输出层节点数量
learningRate = 0.08 #学习率
n = neuralNetwork(inputNodes, hiddenNodes, outputNodes, learningRate)
dataFile = open("NNone/mnist_train.csv", 'r')
dataList = dataFile.readlines()
dataFile.close()
epochs = 5
for i in range(epochs):
for record in dataList:
allValues = record.split(',')
inputs = (numpy.asfarray(allValues[1:]) / 255.0 * 0.99) + 0.01
targets = numpy.zeros(outputNodes) + 0.01
targets[int(allValues[0])] = 0.99
n.train(inputs, targets)
#定义混淆矩阵 行号为预测值 列号为真实值
result = numpy.zeros([10, 10])
numTrue = []
numPredict = []
testDataFile = open("NNone/mnist_test.csv", 'r')
testDataList = testDataFile.readlines()
print(type(testDataList))
testDataFile.close()
testWrongFile = open("NNone/testWrong.csv", 'w+', newline='')
# print(dataList[0])
scorecard = []
for record in testDataList:
allValues = record.split(',')
saveWrongData = allValues.copy()
correctValue = int(allValues[0]) #实际值
inputs = (numpy.asfarray(allValues[1:]) / 255.0 * 0.99) + 0.01 #归一化
outputs = n.predict(inputs)
label = numpy.argmax(outputs) #预测值
result[label, correctValue] += 1 #混淆矩阵
numTrue.append(correctValue)
numPredict.append(label)
if (label == correctValue):
scorecard.append(1)
else:
scorecard.append(0)
writer = csv.writer(testWrongFile)
saveWrongData[0] = label
writer.writerow(saveWrongData)
testWrongFile.close() #关闭文件
scorecardArray = numpy.asarray(scorecard)
print(scorecardArray.sum())
print(scorecardArray.size)
print("准确率:", scorecardArray.sum() / scorecardArray.size)
print(result)
使用sklearn中的方法做出混淆矩阵
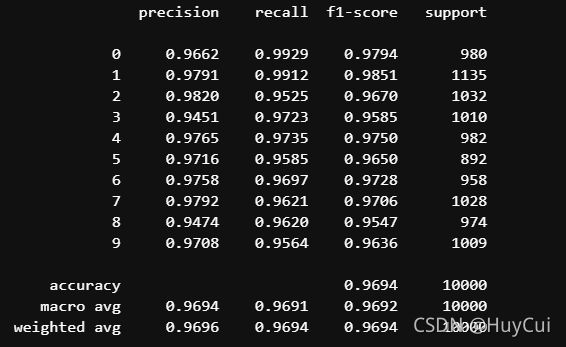
from sklearn.metrics import classification_report
target_names = [str(i) for i in range(10)]
print(classification_report(numTrue, numPredict, target_names=target_names,digits=4))