数据结构和算法之二：栈和队列

数据结构基础之栈和队列

上一文中，我们学习了数组和链表，它们两个是存储数据的最底层结构，是功能完全的线性表。栈和队列是受限的线性表，啥叫功能完全，功能受限呢？数组和链表，我们可以对里面任意位置上的元素进行任意的操作，不受任何限制，而栈和队列，其内部也是数组或链表实现，但是对外暴露的操作接口是有限的，栈只能在栈顶进行压栈和出栈操作，队列只能队尾插入，队头出队操作。

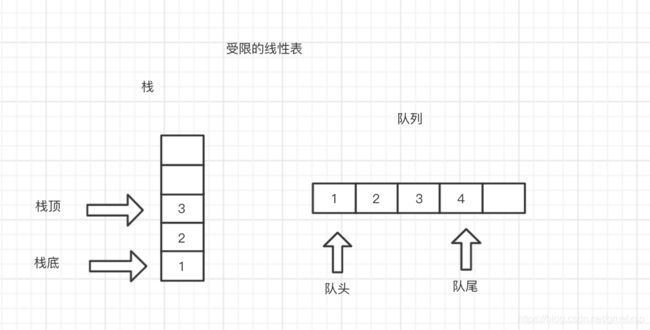
栈和队列的结构示意

为啥有了功能全面的，更加灵活的数组和链表了，为啥还要搞功能受限的结构出来呢？

这是因为在特定的应用场景下， 栈和队列用起来更加简单，也跟贴近业务含义。

栈

栈的特点是进先出即Last In First Out （LIFO），就好比我们在放盘子的时候都是从下往上一个个放，拿的时候是从上往下一个个的那，不能从中间抽，最上面的盘子就是栈顶。

为了加深理解，我们通过数组实现一个简单的栈。

/**
 * 栈接口
 */
public interface MyStack<Item> {

    /**
     * 压栈操作
     * @param item
     */
    void push(Item item);

    /**
     * 出栈操作
     * @return
     */
    Item pop();

    /**
     * 栈元素个数
     * @return
     */
    int size();

    /**
     * 是否空栈
     * @return
     */
    boolean isEmpty();

}

基于数组的栈实现：

/**
 * 基于数组实现的栈
 */
public class ArrayStack<Item> implements MyStack<Item> {
    private int capacity;
    private Item[] elements;  //元素数组
    private int position = -1; //栈顶位置，初始位置为-1，不指向任何数组元素，此时为栈为空

    public ArrayStack() {
        this(16);
    }

    public ArrayStack(int capacity) {
        this.capacity = capacity;
        elements = (Item[]) new Object[capacity];
    }

    @Override
    public void push(Item item) {
        position++;   //栈顶往上生长
        //检查是否需要扩容
        needResize();
        elements[position] = item;  //栈顶位置设置新值
    }

    private void needResize() {

        if(position > elements.length-1){
            resize(elements.length * 2);  //扩一倍
        }
        else if(position < elements.length / 1.75  &&  elements.length > capacity){ //空闲一半以上时，进行缩容。
            resize(elements.length / 2); //缩一倍
        }

    }

    /**
     * 重置数组大小
     * @param newSize
     */
    private void resize(int newSize) {
        Item[] temp = (Item[]) new Object[newSize];
        for (int i = 0; i < elements.length; i++) {
            temp[i] = elements[i];
        }
        elements = temp;
    }

    @Override
    public Item pop() {
        if (isEmpty()) {
            return null;
        }
        Item topElement = elements[position];
        elements[position] = null; //清除引用，避免内存泄露。
        position--; //栈顶往下收缩

        needResize(); //是否需要缩容。

        return topElement;
    }

    @Override
    public int size() {
        return position+1;
    }

    @Override
    public boolean isEmpty() {
        return position==-1;
    }

    public static void main(String[] args) {
        MyStack<Integer> stack = new ArrayStack();
        stack.push(10);
        stack.push(2);
        stack.push(3);

        System.out.println(stack.pop());
        System.out.println(stack.pop());
        System.out.println(stack.pop());
        System.out.println(stack.pop());

    }
}

有了以上栈的一些知识之后，我们来看下如何用栈来巧妙的解决括号匹配的问题，即判断一个字符串，是否符合括号原则，比如[{(()()}] 是符合的 {{[]]]}} 不符合。

用栈来解决这个问题非常简单，一个一个解析字符串， 当发现是左括号之一时压栈，当发现是右括号之一时，与栈顶元素匹配，如果是一对，则消掉，如果不匹配，则表达式不合法。你可以在本子上画图理解一下。

这个问题的代码如下:

/**
 * 符号匹配检测工具
 *   判断一个字符串，是否符合括号原则，比如
 *   [{(()()}] ok  {{[]]]}} not ok。
 *
 *   思路，利用栈实现  O(n)
 *   一个一个解析字符串， 当发现是左括号之一时压栈，
 *   当发现是右括号之一时，与栈顶元素匹配，如果是一对，则消掉，如果不匹配，则表达式不合法。
 *   整个字符串解析完后，如果栈为空，合法；如果不为空，表名左括号多了，不合法。
 */
public class SymbolMatchTool {

    public static boolean isMatched(String str){
        MyStack<Character> stack = new ArrayStack<>(32);

        for (char c : str.toCharArray()) {
            switch (c) {
                case '[':
                case '{':
                case '(':
                    stack.push(c);
                    break;
                case ']':
                    if (!isTopEleIsCharacter(stack, '[')) {
                        return false;
                    }
                    break;
                case '}':
                    if (!isTopEleIsCharacter(stack, '{')) {
                        return false;
                    }
                    break;
                case ')':
                    if (!isTopEleIsCharacter(stack, '(')) {
                        return false;
                    }
                    break;
                default:
                    break;
            }

        }

        if (stack.isEmpty()) {
            return true;
        }

        return false;
    }

    private static boolean isTopEleIsCharacter(MyStack<Character> stack,Character target) {
        Character topEle = stack.pop();
        if(topEle == null || !topEle.equals(target)){
            return false;
        }
        return true;
    }


    public static void main(String[] args) {
        String s = "[[(){[]}]]";
        System.out.println(SymbolMatchTool.isMatched(s));
        s = "[[sdfalajf()asdjf;a{[ljdfsaf]}sfdlkja;f2323]]";
        System.out.println(SymbolMatchTool.isMatched(s));

        s="()(([]}";
        System.out.println(SymbolMatchTool.isMatched(s));
    }
}

如果不是使用栈这种结构来解决，这个问题还真是不好处理的，当然如果你有更好的思路，欢迎留言给我。

另外一个使用栈的经典问题就是 字符串表达式求值 ，比如给你一个字符串“10 + 23 * 5 - 4/8” 这样一个字符串，你怎么将它计算出来呢？

下面我给出下思路， 你可以花点时间自己实现一波。

* 表达式求值计算。
*   不考虑()的情况。只支持加减乘除操作
*
* 简化版，如果只有一种优先级操作，比如只有加减计算，那么只需要一个栈就可以实现。
* 一个一个解析字符串的表达式，如果是符号，则压栈；
* 如果是数字，判断栈是否为空栈（为空表示第一次开始解析），为空压栈，不为空则弹出两个（一个符号，一个是前一个操作数）
* 计算后压栈回去。直到表达式被解析完成，结果也计算完成了。
*
* 加强版，如果操作符号有优先级的情况，比如有加减乘除时，需要两个栈才能实现。
* 思路：
* 一个栈用于放操作数，一个栈用于放操作符号。
* 一个一个解析字符串的表达式，如果是数值，则在操作数栈压栈；
* 如果是符号，那么判断符号的优先级是不是高于 当前操作符号栈的栈顶符号优先级，如果高于，则符号压栈；
*    如果优先级低于等于栈顶符号优先级，则分别从两个栈中弹出两个操作数和一个符号，计算后结果压入操作数栈。
* 直到表达式被解析完成，此时需要判断符号栈是否空（或者操作数栈多余1个元素），
* 如果不为空，则重复分别从两个栈中弹出两个操作数和一个符号，计算后结果压入操作数栈，知道没有符号为止。
*

思考题，如何设计一个浏览器的前进和后退功能？

提示，用两个栈。（最好是画图理解）

队列

栈的特点是先进先出即First In First Out （FIFO），就好比我们排队出站，先排的先出，后排的后出，非常好理解。

同样，使用数组来简单实现一个队列，需要注意的是，数组实现的队列，入队的时候数组下标不能无限的往后加吧，因此需要通过控制，循环的使用前面已经出队的空间，同时也可以控制队列的容量。

/**
 * 基于数组实现的循环队列
 * @param 
 */
public class ArrayQueue<Item> implements MyQueue<Item> {

    int head = 0; //队头下标
    int tail = 0; //队尾下标
    int cap;  //数组长度
    Item[] data; //数组

    public ArrayQueue(int cap) {
        this.cap = cap;
        data = (Item[]) new Object[cap];
    }

    @Override
    public void put(Item item) {
        if((tail+1)%cap == head)  
            return;
        data[tail] = item;
        tail = (tail+1) % cap;  //下标映射
    }

    @Override
    public Item pop() {
        if(isEmpty()){  //空了
            return null;
        }
        Item item = data[head];
        head = (head+1) % cap; //下标映射
        return item;
    }

    @Override
    public boolean isEmpty() {
        return head == tail;
    }

    @Override
    public int size() {
        return tail >= head
                    ? tail - head           //tail在前， head在后的情况
                    : cap - (head+1) + (tail+1); //tail在后， head在前的情况。
    }

    public static void main(String[] args) {
        MyQueue<Integer> queue = new ArrayQueue(4);
        queue.put(1);
        queue.put(2);
        queue.put(3);
        System.out.println(queue.size());
        System.out.println();

        queue.put(4); 

        System.out.println(queue.pop());
        System.out.println(queue.pop());
        System.out.println(queue.pop());
        System.out.println();

        queue.put(5);
        queue.put(6);
        System.out.println(queue.size());
        System.out.println();

        System.out.println(queue.pop());
        System.out.println(queue.pop());
        System.out.println(queue.pop());

        System.out.println(queue.size());

    }
}

队列的应用就非常广泛了，小到我们自己内部应用的队列使用，比如线程池中的阻塞队列；大到消息中间件，如rabbitmq，rockmq，kafka等，都是使用了队列的思想。

那么，你能使用链表来实现一个自己的队列吗？它的实现比数组简单些。