能发动1次能力，从0列走到N-1列，走过的最大路径和是多少？

能发动1次能力，从0列走到N-1列，走过的最大路径和是多少？

提示：DP4：业务限制类模型
动态规划有四种尝试模型：尝试暴力递归代码，最后改为傻缓存或者动态规划DP代码；
DP1：从左往右的尝试模型【分析i从0–N如何如何】
DP2：从L–R范围上的尝试模型【分析范围上以i开头或者以i结尾如何如何】
DP3：样本位置对应模型【2个串，或2个数组这种，分析对应0–i，0–j上以i，或j结尾的子组、子串、子序列如何如何】
DP4：业务限制类模型【限定几种业务情况如何如何】

---

---

题目

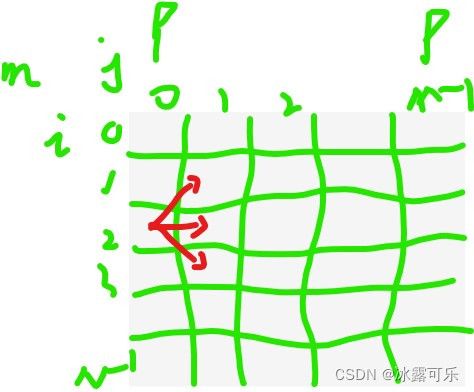
matrix矩阵N行M列，里面都是int数值，路径奖励，骑士从左边j=0列出发，期间，
1）只能使用一次能力，使得mij变为-mij，
2）一旦路径和小于0，则游戏结束，返回-1
3）走的过程中，骑士只能往右上角，右边，和右下角走。
如果骑士能顺利走到M-1列的话，请问他能获得的最大路径和是多少？

---

一、审题

只有三个方向可以走，往往就是限制条件，这时候敏感地想到业务限制模型DP；

假如j=0列时，里面的mij全是负数，比如-100，那起步你就得用能力变正，否则你走不动，因为路径和小于0游戏终止

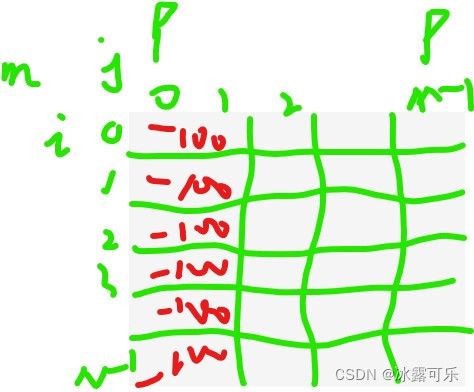
如果能顺利到M-1列，那把路上可能发动能力，也可能不发动能力的情况，路径和，最大值返回，否则返回-1；

二、解题

在任意位置ij，不妨设一个函数，返回最大值int f(arr,i,j)，来到ij之后，我的累加和最大是多少？
我们要的结果肯定是int f(arr,i,M-1)，要最后一列的结果。
则求的时候，得往前推i，j-1列那些情况
而且只来自于三个方向，最基本的情况是i，j=0列那，决定用能力还是不用；

我们这么思考：
如何计算ij时的最大累加和？如果0–j用过能力，则设为yes，没有发动过能力，则设为no；

这里就不得不问：
请问你之前走过0–j-1过程中，有没有发动过能力，有发动过的话，我求j的最大累加和时，一定不能发动能力，你没有发动过我可以在j列时考虑发动能力。

注意，求j的最大累加和yes和no过程中，得看看骑士从哪个方向来的，是左上角【i-1,j-1】，左边【i,j-1】，还是左下角【i+1,j-1】？分清楚这三种业务限制，也就好办了。

算法大流程：

暴力递归f的代码：
——base case：在j==0时，发动为yes = -m[i,0]，不发动为no = m[i,0]；放入1*2维的结果返回即可
——其余的j>0；
分三个方向来的结果，f(arr,i-1,j-1)左上角，f(arr,i,j-1)左边，f(arr,i+1,j-1)左下角，依次判断，他们可能来自这些方向吗？也就是不越界，然后不断更新最大值在preUse【发动过能力的结果】，preNoUse【没法动过能力的结果】中
——最后假设yes=-1,no=-1，如果preUse和preNoUse不是-1，则可以更新yes和no，
只是要注意，yes的话，是preUse（之前就发动过了）和preNoUse-m[i,j]（也就是本次才发动能力）的最大值
而no是一直就没有发动，本次也不发动能力的值即：preNoUse+mij
返回2元数组；

最后main中如何调用呢？
你不是有N行吗？到底哪一行出发能搞到最大值呢？fori遍历一遍拿出最值即可，非常简单的。

暴力递归代码如下：

//preUnUsed,preUsed---作为返回结果
    public static int[] process(int[][] matrix, int i, int j){
        if (j == 0) return new int[] {matrix[i][j], -matrix[i][j]};//j==0，本列不用能力，用能力就俩情况

        //j>0，从左侧三条路来了，选哪个呢
        //正左侧
        int[] preSum = process(matrix, i, j - 1);
        int preUnUsed = preSum[0];
        int preUsed = preSum[1];//拿到结果，跟另外两条路pk去

        if (i - 1 >= 0){
            //左上角有效
            preSum = process(matrix, i - 1, j - 1);
            preUnUsed = Math.max(preUnUsed, preSum[0]);//一直都不用能力的情况
            preUsed = Math.max(preUsed, preSum[1]);//用过一次能力的情况
        }
        if (i + 1 < matrix.length){
            //左下角有效
            preSum = process(matrix, i + 1, j - 1);
            preUnUsed = Math.max(preUnUsed, preSum[0]);//一直都不用能力的情况
            preUsed = Math.max(preUsed, preSum[1]);//用过一次能力的情况
        }

        //整理我自己，为下一次做准备---初始为-1，怕上面无效，我也得无效
        int yes = -1;
        int no = -1;
        if (preUnUsed >= 0){
            //之前没有用能力，不过一直有效的，我这次用还是不用呢
            yes = preUnUsed - matrix[i][j];//用我这次
            no = preUnUsed + matrix[i][j];//继续不用
        }
        if (preUnUsed >= 0){
            //对于用能力的情况，可能之前就用过了，本次不可再用，pk一下之前没用，但是用本次的情形
            yes = Math.max(yes, preUsed + matrix[i][j]);
        }

        return new int[] {no, yes};//返回，和属性DP类似呢
    }

主函数调用代码：

//主函数，枚举最左侧每一个位置，然后get最大值
    // 不用每个格子都去求最值吧，只需要看最后一列那个的情况，反正要去调递归
    public static int maxSumOfSnake2(int[][] matrix){
        if (matrix == null || matrix[0] == null || matrix.length == 0 || matrix[0].length == 0) return 0;

        int N = matrix.length;
        int M = matrix[0].length;
        int ans = 0;
        for (int i = 0; i < N; i++) {
            //每个行，一个位置，从0列开始走
            //但是因为j只能往右，所以j可以迭代这个ans过去
                int[] preSum = process(matrix, i, M -1);
                ans = Math.max(ans, Math.max(preSum[0], preSum[1]));//要不要发动能力，取最好的
        }
        return ans;
    }

暴力递归改为动态规划的傻缓存代码：——速度快

//改为傻缓存：
    //preUnUsed,preUsed---作为返回结果
    public static int[] processDP(int[][] matrix, int i, int j, int[][][] dp){
        if (j == 0) {
            dp[0][i][i] = matrix[i][j];
            dp[1][i][i] = -matrix[i][j];
            return new int[] {dp[0][i][i], dp[1][i][i]};//j==0，本列不用能力，用能力就俩情况
        }

        if (dp[0][i][i] >= 0 && dp[0][i][i] >= 0) return new int[] {dp[0][i][i], dp[1][i][i]};

        //j>0，从左侧三条路来了，选哪个呢
        //正左侧
        int[] preSum = process(matrix, i, j - 1);
        int preUnUsed = preSum[0];
        int preUsed = preSum[1];//拿到结果，跟另外两条路pk去

        if (i - 1 >= 0){
            //左上角有效
            preSum = process(matrix, i - 1, j - 1);
            preUnUsed = Math.max(preUnUsed, preSum[0]);//一直都不用能力的情况
            preUsed = Math.max(preUsed, preSum[1]);//用过一次能力的情况
        }
        if (i + 1 < matrix.length){
            //左下角有效
            preSum = process(matrix, i + 1, j - 1);
            preUnUsed = Math.max(preUnUsed, preSum[0]);//一直都不用能力的情况
            preUsed = Math.max(preUsed, preSum[1]);//用过一次能力的情况
        }

        //整理我自己，为下一次做准备---初始为-1，怕上面无效，我也得无效
        int yes = -1;
        int no = -1;
        if (preUnUsed >= 0){
            //之前没有用能力，不过一直有效的，我这次用还是不用呢
            yes = preUnUsed - matrix[i][j];//用我这次
            no = preUnUsed + matrix[i][j];//继续不用
        }
        if (preUnUsed >= 0){
            //对于用能力的情况，可能之前就用过了，本次不可再用，pk一下之前没用，但是用本次的情形
            yes = Math.max(yes, preUsed + matrix[i][j]);
        }

        dp[0][i][i] = no;
        dp[1][i][i] = yes;

        return new int[] {dp[0][i][i], dp[1][i][i]};//返回，和属性DP类似呢
    }

    //主函数，枚举最左侧每一个位置，然后get最大值//不用每个格子都去求最值吧，只需要看最后一列那个的情况，反正要去调递归
    public static int maxSumOfSnake2DP(int[][] matrix){
        if (matrix == null || matrix[0] == null || matrix.length == 0 || matrix[0].length == 0) return 0;

        int N = matrix.length;
        int M = matrix[0].length;

        int[][][] dp = new int[2][N][M];
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < N; j++) {
                for (int k = 0; k < M; k++) {
                    dp[i][j][k] = -1;
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < N; i++) {
            //每个行，一个位置，从0列开始走
            //但是因为j只能往右，所以j可以迭代这个ans过去
            int[] preSum = processDP(matrix, i, M -1, dp);
            ans = Math.max(ans, Math.max(preSum[0], preSum[1]));//要不要发动能力，取最好的
        }


        return ans;
    }

测试代码：

public static void test(){
        int[][] arr = {
                {-100,-1000,1,2},
                {-100,-1000,1,2},
                {10,   10, 1000,2}
        };
        System.out.println(maxSumOfSnake2(arr));
        System.out.println(maxSumOfSnake2DP(arr));
    }

    public static void main(String[] args) {
        test();
    }

---

总结

提示：本题的重要经验：

1）熟悉和掌握4种重要的DP尝试模型
2）DP4出的题目少，但是要敢于尝试，敢于分析