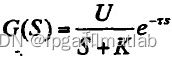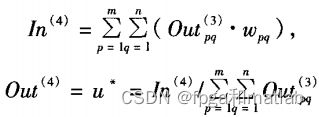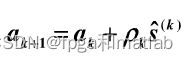【模糊神经网络】基于matlab的模糊神经网络仿真

1.软件版本

matlab2013b

2.系统概述

·第一个模型：

；

·第二个模型

；，U=13.012

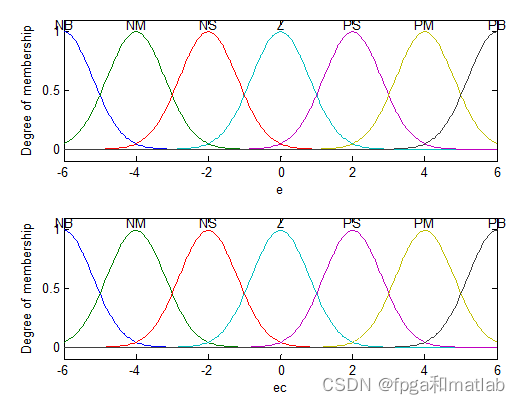
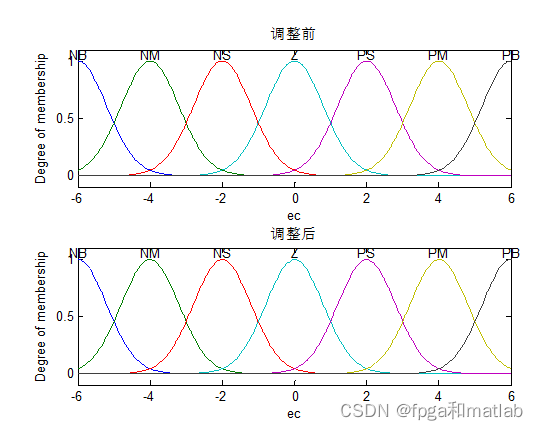
第一：隶属函数的设计

    隶属函数的设计，可以通过模糊编辑器，也可以通过如上的代码进行设计。

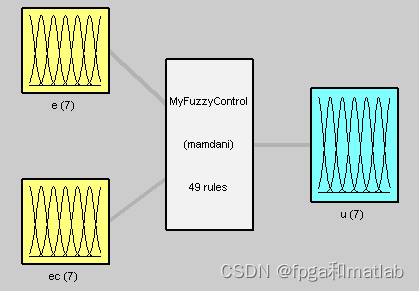
第二：模糊规则的设计

通过输入模糊规则量化表进行设计，所得到的模糊规则如下所示：

1. If (e is NB) and (ec is NB) then (u is PB) (1)

2. If (e is NB) and (ec is NM) then (u is PB) (1)

3. If (e is NB) and (ec is NS) then (u is PM) (1)

4. If (e is NB) and (ec is Z) then (u is PM) (1) 

5. If (e is NB) and (ec is PS) then (u is PS) (1)

6. If (e is NB) and (ec is PM) then (u is PS) (1)

7. If (e is NB) and (ec is PB) then (u is Z) (1) 

8. If (e is NM) and (ec is NB) then (u is PB) (1)

9. If (e is NM) and (ec is NM) then (u is PM) (1)

10. If (e is NM) and (ec is NS) then (u is PM) (1)

11. If (e is NM) and (ec is Z) then (u is PS) (1)

12. If (e is NM) and (ec is PS) then (u is PS) (1)

13. If (e is NM) and (ec is PM) then (u is Z) (1)

14. If (e is NM) and (ec is PB) then (u is NS) (1)

15. If (e is NS) and (ec is NB) then (u is PM) (1)

16. If (e is NS) and (ec is NM) then (u is PM) (1)

17. If (e is NS) and (ec is NS) then (u is PS) (1)

18. If (e is NS) and (ec is Z) then (u is PS) (1)

19. If (e is NS) and (ec is PS) then (u is Z) (1)

20. If (e is NS) and (ec is PM) then (u is NS) (1)

21. If (e is NS) and (ec is PB) then (u is NS) (1)

22. If (e is Z) and (ec is NB) then (u is PM) (1)

23. If (e is Z) and (ec is NM) then (u is PS) (1)

24. If (e is Z) and (ec is NS) then (u is PS) (1)

25. If (e is Z) and (ec is Z) then (u is Z) (1)  

26. If (e is Z) and (ec is PS) then (u is NS) (1)

27. If (e is Z) and (ec is PM) then (u is NS) (1)

28. If (e is Z) and (ec is PB) then (u is NM) (1)

29. If (e is PS) and (ec is NB) then (u is PS) (1)

30. If (e is PS) and (ec is NM) then (u is PS) (1)

31. If (e is PS) and (ec is NS) then (u is Z) (1)

32. If (e is PS) and (ec is Z) then (u is NS) (1)

33. If (e is PS) and (ec is PS) then (u is NS) (1)

34. If (e is PS) and (ec is PM) then (u is NM) (1)

35. If (e is PS) and (ec is PB) then (u is NM) (1)

36. If (e is PM) and (ec is NB) then (u is PS) (1)

37. If (e is PM) and (ec is NM) then (u is PS) (1)

38. If (e is PM) and (ec is NS) then (u is Z) (1)

39. If (e is PM) and (ec is Z) then (u is NS) (1)

40. If (e is PM) and (ec is PS) then (u is NM) (1)

41. If (e is PM) and (ec is PM) then (u is NM) (1)

42. If (e is PM) and (ec is PB) then (u is NB) (1)

43. If (e is PB) and (ec is NB) then (u is Z) (1)

44. If (e is PB) and (ec is NM) then (u is NS) (1)

45. If (e is PB) and (ec is NS) then (u is NS) (1)

46. If (e is PB) and (ec is Z) then (u is NM) (1)

47. If (e is PB) and (ec is PS) then (u is NM) (1)

48. If (e is PB) and (ec is PM) then (u is NB) (1)

49. If (e is PB) and (ec is PB) then (u is NB) (1)

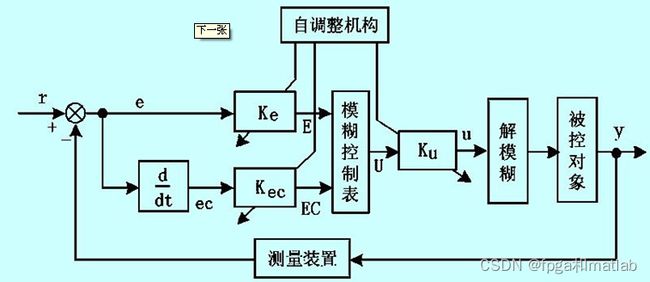
第三：控制闭环的设计

通常，一个传统的模糊控制器的闭环结构如下所示：

模糊控制器的基本结构：

3.部分源码

addpath 'func\'

title_function

%初始化
fnn_parameter;

%被控对象
a1        = 1.2;
b1        = 1;
b2        = 0.8;
b3        = 0;

ta        = 40;
sys       = tf(a1,[b1,b2,b3]);
dsys      = c2d(sys,0.1,'z');
[num,den] = tfdata(dsys,'v');
ts        = 0.1;%采样时间T=0.1

%闭环控制器
for k=1:SIM_times
    k
    time(k) = k*ts;
    %定义输入信号
    yd(k)   = 2;  
    %定义输出信号
    if k < ta
       yn = 0; 
    else
       yn = -den(2)*y1 - den(3)*y2 + num(2)*u1 + num(3)*u2;
    end    
    
    y2   = y1;
    y1   = yn;
    y(k) = yn;
    u2   = u1;
    e2   = e1;
    e1   = yd(k)-yn;
    e(k) = e1;
    ec   =(e1-e2);
    
    x1   =(1-exp(-10*e1))/(1+exp(-10*e1));
    x2   =(1-exp(-ec))/(1+exp(-ec));
    
    %第1层输出
    for i=1:7
        o11(i) = x1;
        o12(i) = x2;
    end
    o1=[o11;o12];
    
    %第2层输出
    for i=1:2
        for j=1:7
            z1(i,j)  =-((o1(i,j)-a(i,j))^2)/(b(i,j));
            o2(i,j)  =  exp(z1(i,j));
        end
    end
    
    %第3层输出
    for j=1:7
        for l=1:7
            o3((j-1)*7+l)=o2(1,j)*o2(2,l);
        end
    end
    
    %第4层输出
    I=0;
    for i=1:49
        I = I + o3(i)*Weight(i)/4;
    end

    o4   = I/(sum(o3));
    u(k) = o4;
    u1   = o4;
    %梯度下降法调整权值
    for i=1:49
        dwp       =  e1*du*o3(i)/(sum(o3));
        %迭代
        Weight(i) =  Weight(i) + eta*dwp;
    end

    %中心值更新
    da11=zeros(1,7);
    for j=1:7
        for l=1:7
            da11(j) =  da11(j)+(o2(2,l)*((Weight((j-1)*7+l)*sum(o3))-I));
        end
        da12(1,j)   = -e1*du*(2*(o1(1,j)-a(1,j))*(o2(1,j)))/((b(1,j)^2)*(sum(o3))^2);
        da1(j)      = (da12(1,j))*(da11(j));
    end
    da21 = zeros(1,7);
    for j=1:7
        for l=1:7
            da21(j) = da21(j)+(o2(1,l)*((Weight((l-1)*7+j)*sum(o3))-I));
        end
        da22(2,j) = -e1*du*(2*(o1(2,j)-a(2,j))*(o2(2,j))/((b(2,j)^2)*(sum(o3))^2));
        da2(j)    = (da22(2,j))*(da21(j));
    end      
    da=[da1;da2];
    for i=1:2
        for j=1:7
            a(i,j)=a(i,j)-eta*da(i,j);
        end
    end             
    a_s(:,:,k) = a;
    
    if k == 1
       a_(:,:,k) = a_s(:,:,1);
    else
       for i = 1:2
           for j = 1:7
               dist_tmp(i,j) = (a_s(i,j,k) - a_(i,j))^2;
           end
       end
       dist = sqrt(sum(sum(dist_tmp))); 
       
       if dist < 0.1
           
          tmps(:,:,1) = a_(:,:,k-1);
          tmps(:,:,2) = a_s(:,:,k);
           
          a_(:,:,k) = mean(tmps(:,:,1:2),3);
       else
          a_(:,:,k) = a_(:,:,k-1);
       end
    end
    
    a = a_(:,:,k);
    
    
    %宽度更新
    db11=zeros(1,7);
    for j=1:7
        for l=1:7
            db11(j)=db11(j)+(o2(2,l)*((Weight((j-1)*7+l)*sum(o3))-I));
        end
        db12(1,j)=-e1*du*(2*(o1(1,j)-a(1,j))^2)*(o2(1,j))/((b(1,j)^3)*(sum(o3))^2);
        db1(j)=(db12(1,j))*(db11(j));
    end
    db21=zeros(1,7);
    for j=1:7
        for l=1:7
            db21(j)=db21(j)+(o2(1,l)*((Weight((l-1)*7+j)*sum(o3))-I));
        end
        db22(2,j)=-e1*du*(2*(o1(2,j)-a(2,j))^2)*(o2(2,j))/((b(2,j)^3)*(sum(o3))^2);
        db2(j)=(db22(2,j))*(db21(j));
    end      
    db=[db1;db2];
    for i=1:2
        for j=1:7
            b(i,j)=b(i,j)-eta*db(i,j);
        end
    end      
    b_s(:,:,k) = b;
    
    if k == 1
       b_(:,:,k) = b_s(:,:,1);
    else
       for i = 1:2
           for j = 1:7
               dist_tmp(i,j) = (b_s(i,j,k) - b_(i,j))^2;
           end
       end
       dist = sqrt(sum(sum(dist_tmp))); 
       
       if dist < 0.1
          tmps(:,:,1) = b_(:,:,k-1);
          tmps(:,:,2) = b_s(:,:,k);
           
          b_(:,:,k) = mean(tmps(:,:,1:2),3);
       else
          b_(:,:,k) = b_(:,:,k-1);
       end
    end    
    
    
    b = b_(:,:,k);
    
    %算法
    s11 = y1;
    s12 = y2;
    s13 = u1;
    s14 = u2;
    s1  =[s11;s12;s13;s14];
    
    for i=1:5
        net2(i) = w2(i,:)*s1 + theta2(i);
        s2(i)   = (1-exp(-net2(i)))/(1+exp(-net2(i)));
    end
    
    net3  = w3*s2+theta3;
    yg    = am*(1-exp(-net3))/(1+exp(-net3));

    for i=1:5
        delta2(i)=0.5*(1-s2(i))*(1+s2(i));
    end
    
    delta3=0.5*am*(1-yg/am)*(1+yg/am);
    
    for i=1:5
        theta22(i) = theta2(i)-theta21(i);
        theta21(i) = theta2(i);
        theta2(i)  = theta2(i)+eta1*(yn-yg)*delta3*w3(i)*delta2(i)+beta1*theta22(i);
    end
    
    theta32 = theta3-theta31;
    theta31 = theta3;
    theta3  = theta3+eta1*(yn-yg)*delta3+beta1*theta32;
    
    for i=1:5
        for j=1:4
            w22(i,j) = w2(i,j)-w21(i,j);
            w21(i,j) = w2(i,j);
            w2(i,j)  = w2(i,j)-eta1*(yn-yg)*delta3*w3(i)*delta2(i)*s1(j)+beta1*w22(i,j);
        end
        w32(i) = w3(i)-w31(i);
        w31(i) = w3(i);
        w3(i)  = w3(i)-eta1*(yn-yg)*delta3*s2(i)+beta1*w32(i);
    end
    a2   = am-a1;
    a1   = am;
    am   = am+eta1*(yn-yg)*yg/am+beta1*a2;
    sum1 = 0;
    for i=1:5
        sum1 = sum1 + w3(i)*delta2(i)*w2(i,3);
    end
    du = delta3*sum1;
    
end            

figure;
plot(time,y,'r', time,yd,'b');
grid on

figure;
subplot(121);
plot(a_s(1,:,SIM_times),a_s(2,:,SIM_times),'o'); 
grid on
axis square
subplot(122);
plot(b_s(1,:,SIM_times),b_s(2,:,SIM_times),'o'); 
grid on
axis square

save Simu_Results\fnn_result.mat time y

save Simu_Results\nfis.mat a b

    这里重点介绍一下模糊神经网络控制器的设计，

第一：四层化神经网络层的结构设计：

第1层：

第2层：

第3层：

第4层：

第二：利用梯度下降法进行权值更新

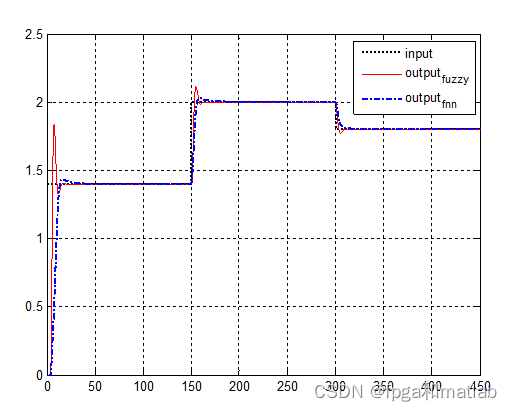
4.仿真结果

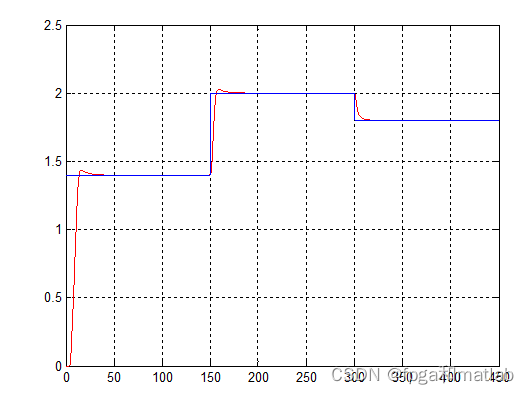
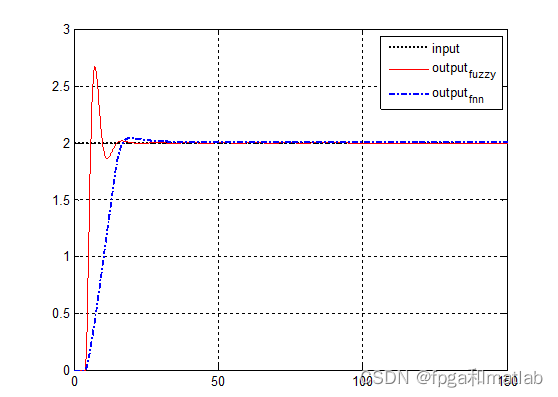
模糊控制效果图（模型一）：

 模糊控制效果图（模型二）：

    隶属函数如下所示：

 

 

 

 

 

 A05-06