数据结构：BF算法 & KMP算法

BF算法

---

BF(Brute Force)算法，即暴力算法，是普通的串的模式匹配算法，BF算法是一种蛮力算法

BF算法的思想就是将目标串S(主串)的第一个字符与模式串T(子串)的第一个字符进行匹配，若相等，则继续比较S的第二个字符和 T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果

BF算法效率并不高，因为每次没找到，主串都要回退到上一次开始的下一个位置

BF算法时间复杂度O(m*n) 空间复杂度O(1)

BF算法图解如下：

C代码如下：

//返回 子串T 在 主串S 中第pos个字符之后的位置
//时间复杂度：O(m*n) 空间复杂度：O(1)

int BF(const char* S, const char *T,int pos)  //S主串，T子串
{
	if (S == NULL || T == NULL || pos < 0 || pos >= strlen(S))
	{
		return -1;
	}

	int i = pos;
	int j = 0;
	int len1 = strlen(S);//主串长度
	int len2 = strlen(T);//子串长度

	while(i<len1&&j<len2)
	{
		if (S[i] == T[j])
		{
			i++;
			j++;
		}
		else
		{
			/*回退到本次开始的下一个位置（i-j+1)，j回退到0*/
			i = i - j + 1;
			j = 0;
		}
	}

	if (j >= len2)  //子串走完即为查找成功
		return i - j ;
	else  
		return -1;
}

BF算法的效率不高，时间复杂度O(m*n)，每次匹配失败主串游标 i 都要回退到本次开始的下一个位置，子串游标 j 要回退到0。而KMP算法改进了i，j的回退，避免了不必要的回溯，提高了效率，时间复杂度降到了O(m+n)

KMP算法

---

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，取他们姓首字母，即为KMP算法。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的

KMP算法时间复杂度O(m+n) 空间复杂度O(n)

在BF算法中，每次失配，主串游标 i 都要回退到 i-j+1，子串游标 j 要回退到0

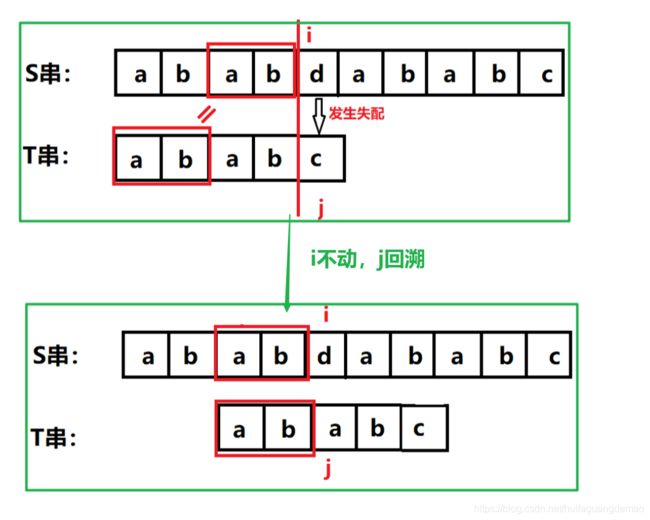
但是其实在出现失配时，可以让 i 不回退，j 回退到该退的位置即可，如下图BF算法示意图中，第一次失配后，i 回溯到 i-j+1，j 回溯到0，但是我们可以发现之后的比较中，i 又回到了之前的位置，j 位置改变了而已（下图红框）

KMP算法就是在出现失配时，让主串游标 i 不回退，利用之前失败的信息，让子串游标 j 退回到合适的位置

所以关键就是求出失配后子串游标 j 应该回溯的位置，我们用一个next数组来存储子串每个位置对应的 j 应该回溯的位置

把上面BF算法代码直接拷贝过来，修改 i,j 的回退即可完成KMP算法的大框架

int KMP(const char* S, const char *T,int pos)  //S主串，T子串
{
	if (S == NULL || T == NULL || pos < 0 || pos >= strlen(S))
	{
		return -1;
	}

	int i = pos;
	int j = 0;
	int len1 = strlen(S);//主串长度
	int len2 = strlen(T);//子串长度

	while(i<len1&&j<len2)
	{
		if (S[i] == T[j])
		{
			i++;
			j++;
		}
		else//修改i，j的回退
		{
			//i不回退
			//j要退到k
		}
	}

	if (j >= len2)  //子串走完即为查找成功
		return i - j ;
	else  
		return -1;
}

接下来的任务就是要把 j 回退的位置 k 给求出来，即求出next数组

---

求next数组

预备知识：字符串的前缀、后缀

前缀：首字符开始的子串
真前缀：首字符开始的子串，但不包含原串本身
后缀：以尾字符结尾的子串
真后缀：以尾字符结尾的子串，但不包含原串本身
例：ababc
前缀：a、ab、aba、abab、ababc
真前缀：a、ab、aba、abab
后缀：c、bc、abc、babc、ababc
真后缀：c、bc、abc、babc

如下例中

在 i 是4,j 是4时发生失配，但是我们发现失配前的S串真后缀与T串真前缀出现相等，相等的部分就不用比较了，因此直接从相等的后面开始继续比较就好（如下图），即j回溯到相等串的后面，即j下标变为相等串的长度，所以关键就是求每次失配这个相等串的长度 k

又因为第一次比较中，失配前的四个字符S串与T串都是一一对应相等的，因此S串的真后缀也是T串的真后缀，因此k就是T串失配前的串的真前缀与真后缀相等时的长度值

因而求k值的方法就是：在子串失配前找到相等的真前缀与真后缀，其长度就是k或者可以这样描述：

在子串失配前找到最长两个相等的真子串，这两个真子串满足如下特点：
1.一个串以首字符开头
2.另一个串以失配前的最后一个字符作为结尾
k就是该真子串的长度

上例T串每个字符对应的k值如下：
规定：next[0]=-1,next[0]=0

模式串T串	a	b	a	b	c
next	-1	0	0	1	2

注意：还有一种常用的next数组表示，next[0]放的是0，next[1]是1，后续每一个k值都比上表里的大1，但是算法思路都是一样的，二者皆可，为便于编码，这里采用next[0] = -1这种方法

手动已经可以求出next数组的值了，接下来就是用程序具体求出next数组：

1. 对于任意串都可以确定其next[0] = -1,next[1] = 0;
2. 设next[j] = k，即下标 j 之前的串的真前缀与真后缀相等的长度为k，即P0…Pk-1 == Pj-k…Pj-1，求next[j+1]
3. 情况一：若Pk == Pj，则P0…Pk-1Pk = Pj-k…Pj-1Pj，即j+1对应的真前缀与真后缀相等时的值是k+1，即next[j+1] = k+1
4. 情况二：若Pk != Pj，如下图，把P0…Pk放到Pk…Pj下面来看，则又要用到之前的思想，主串游标j不动，子串游标k往回退到合适位置，而子串游标k回退的位置在之前已经求出来了，是next[k]，所以k回退到next[k]，即k=next[k]，之后Pk再与Pj比较，如此往复直到Pk==Pj或k回溯到-1，k回溯到-1说明没有相等的真前缀与真后缀，那么next[j+1]赋值为0即可，或者next[j+1]=k+1，这也是next数组的第一个k值放-1的好处
   
5. next数组的C代码：

static void GetNext(const char* T,int * next)  //根据子串T获取它的next数组(用来存放所有的k值)
{
	int lenT = strlen(T);
	if(lenT == 1)   {	next[0] = -1; return;	}
	next[0] = -1;
	next[1] = 0;
	int j = 1;
	int k = 0;

	while (j + 1 < lenT)
	{
		if (k == -1 || T[k] == T[j])//Pk==Pj，k为-1就没必要回退了
		{
			/*
			next[j + 1] = k + 1;
			j++;
			k++;
			*/
			next[++j] = ++k;
		}
		else//Pk != Pj
		{
			k = next[k];//主串游标j不动，子串游标k往回退
		}
	}
}

---

至此，next数组已经求出，即主串游标不动、子串游标j回退的位置已经求出，最后把j = next[j]放入失配条件下，KMP算法就完成了，KMP算法全部的C代码如下：

static void GetNext(const char* T, int * next);  //声明获取next数组的函数

int KMP(const char* S, const char *T, int pos)  //S主串，T子串
{
	if (S == NULL || T == NULL || pos < 0 || pos >= strlen(S))
	{
		return -1;
	}

	int i = pos;
	int j = 0;
	int len1 = strlen(S);//主串长度
	int len2 = strlen(T);//子串长度


	int *next = (int *)malloc(len2 * sizeof(int));
	GetNext(T, next);//求next数组

	while (i < len1&&j < len2)
	{
		if (j==-1 || S[i] == T[j])
		{
			i++;
			j++;
		}
		else
		{
			//i不回退
			j = next[j];//j回退到k
		}
	}
	free(next);
	if (j >= len2)  //子串走完即为查找成功
		return i - j;
	else
		return -1;
}
static void GetNext(const char* T, int * next)  //根据子串T获取它的next数组(用来存放所有的k值)
{
	int lenT = strlen(T);
	if(lenT == 1)   {	next[0] = -1; return;	}
	next[0] = -1;
	next[1] = 0;
	int j = 1;
	int k = 0;

	while (j + 1 < lenT)
	{
		if (k == -1 || T[k] == T[j])//Pk==Pj，k为-1就没必要回退了
		{
			/*
			next[j + 1] = k + 1;
			j++;
			k++;
			*/
			next[++j] = ++k;
		}
		else//Pk != Pj
		{
			k = next[k];//主串游标j不动，子串游标k往回退
		}
	}
}