信息论与编码 通信工程 曹瑞珂 P02014263

 1.对于信源的发送和接收，我们日常生活中有哪些应用？举例说明其工作原理与信息论的关系。

信源是向通信系统提供消息的人或者机器。信源输出的是以符号形式出现的具体消息，它载荷信息。输出的消息可分为两大类：离散消息和连续消息。消息的发送通过编码实现，编码主要是为了与信道能传输的信息匹配，也即符号匹配，同时也是为了压缩信息的冗余度；消息的接收通过译码实现。生活中的应用有很多，以打电话为例，信源就是话筒，人们说话时发出的声音经过话筒内部的转换，变成了可以传输的电压信号，并且经过进一步的编码使其能在电话线或者通过电磁波来传输。而且，声音信号是连续信号，其极限熵趋于无穷，要想在信道上传输声音信号，就必须容忍一定程度的失真，也就是要对信号进行抽样，在这个过程中，对信源打出的信息进行一定程度的压缩，用来提高通信系统传输过程的有效性。

2.在面临香农公式被逼近极限，未来无线通信会朝着哪些方向发展？结合信息论谈一下自己的见解。

香农公式被逼近极限，也就是通信信道的容量在理论上的极限值已经被逼近，通信系统信道中的信息传输速率已经达到极限，在点到点的信道容量方面已经趋近容量限值。在我看来，未来通信技术的发展，剩下的只是通信频道量的扩张，也就是发展多输入多输出系统（MIMO）。课本3.5节的内容表明，在功率和带宽固定时，MIMO系统的最大容量和容量上限随最小天线数的增加而线性增加，因此，MIMO对于提高无线通信系统的容量具有极大的潜力。此外，语义通信也是解决这一问题的一个有效的途径。语义通信是面向信号语义的通信，其本质是传递由语义符号表达的信息，这些符号能够让接受者秒懂其中的含义。语义通信的信号接收双方凭借本地的语义知识库，通过传输极少的内容，各自分别编码和解码，实现大量信息的准确与快速传递。跟科幻剧和谍战剧中的黑科技传输形式类似，极少内容量的传输，就可以完成信息的传递，不仅降低信息传递和理解的时间，也能保证实时保真的通信质量。

3.在通信系统中，除了常见的高斯白噪声还有哪些噪声会对我们无线传输造成影响？

（1）白噪声：在通信系统中，经常碰到的噪声之一就是白噪声。所谓白噪声是指它的功率谱密度函数在整个频域内是常数，即服从均匀分布。换句话说，此信号在各个频段上的功率是一样的，由于白光是由各种频率（颜色）的单色光混合而成，因而此信号的这种具有平坦功率谱的性质被称作是“白色的”，此信号也因此被称作白噪声。相对的，其他不具有这一性质的噪声信号被称为有色噪声。

（2）高斯噪声：高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声。常见的高斯噪声包括起伏噪声、宇宙噪声、热噪声和散粒噪声等等。除常用抑制噪声的方法外，对高斯噪声的抑制方法常常采用数理统计方法。

（3）窄带高斯噪声：当高斯噪声通过以为中心角频率的窄带系统时，就可形成窄带高斯噪声。所谓窄带系统是指系统的频带宽度远远小于其中心频率的系统，即 的系统。这是符合大多数信道的实际情况的。窄带高斯噪声的特点是频谱局限在 附近很窄的频率范围内，其包络和相位都在作缓慢随机变化。如用示波器观察其波形，它是一个频率近似为 ，包络和相位随机变化的正弦波。因此，窄带高斯噪声 可表示为。式中,  为噪声 的随机包络; 为噪声 的随机相位。相对于载波 的变化而言，它们的变化要缓慢的多。

（4）正弦信号加窄带高斯噪声：信道中加性噪声无时不在，信号经过信道传输总会受到它的影响。因此，接收端收到的信号实际上是信号与噪声的合成波。通信系统中，常常碰到的合成信号具有正弦信号加窄带高斯噪声的形式，如在分析2ASK、2FSK、2PSK等信号抗噪声性能时，其信号均为 形式。下面研究该合成信号的包络及其相位的统计特性。正弦信号加上信道噪声后的合成信号可以表示为：

式中，为信道加性窄带高斯噪声；,     

分别为合成信号的随机包络和随机相位。

（5）散弹噪声：散弹噪声是一种发生于有源器件内部的载流子或电子发射的随机性而形成的散弹效应起伏过程。分析表明，散弹噪声可以认为是由大量宽度甚窄的脉冲的随机叠加。散弹噪声的功率谱直到f=2.2×Hz都是基本上平坦的带限白噪声。就实用带宽范围而言，可以认为是白色噪声。散弹噪声最典型的例子是饱和二极管中电子发射的随机性形成在直流分量电流 上下的电流起伏。如图所示。由图可知，电流 , 就是散弹噪声。由中心极限定理可以证明，散弹噪声 是一高斯过程，且均值为零。 的起伏是非常微弱的，显然，只有在研究接收微弱信号或讨论微弱信号放大等场合，才有考虑这种散弹噪声的必要。

（6）余弦信号加窄带高斯噪声：余弦信号和窄带高斯噪声的随机包络服从广义瑞利分布（也称莱斯分布)。若信号幅度A→0时，其随机包络服从瑞利分布。余弦信号加窄带高斯噪声的随机相位分布与信道中的信噪比有关，当信噪比很小时，它接近于均匀分布。

（7）热噪声：热噪声通常又称为电阻热噪声。它的功率谱均匀分布的频率范围约为 Hz，通常认为它是典型的白噪声。我们知道，在一定温度下，任何物体都在不断地骚动，骚动着的物体、通过力和电磁的方式与周围环境交换能量。按照统计力学的能量等配定律，在温度T之下，一个运动自由度的能量平均值等于1/2KT，这里K是玻耳兹曼常数，K=1.38×J/K;T是热力学温度。热骚动同样以电的形式在电路中表现出来。电路中的电流或电路两点之间的电位差，被发现在不停地起伏，在处于一定温度下的电路中，这种起伏是无法避免的。因为热就是物质的无规则的运动。电路中的起伏，在高灵敏度的情况下，很早就被人所觉察。当存在于一个电路中的信号的振幅小到与这种随机热骚动导致的电压起伏具有相同数量级时，这种热起伏将明显地为干扰信号。人们发现，所关心的物理量的起伏状况，包括起伏方差，以及起伏过程的快慢程度（即起伏过程的自相关时间)与所关心的电路的各种参量有关。因此，有必要寻求出一个计算这些起伏特征的方法。这个方法就是应用热噪声的奈奎斯特定理。线性电路中，热噪声的计算方法可归结为: 在温度T下，任意线性网络内任—节点电压或支路电流的热噪声的功率谱为：

       等效的噪声电压源功率谱S(w) = 2KTR                  等效的噪声电流源功率谱S(w) = 2KTG

式中，G=1/R，K是玻耳兹曼常数，T是热力学温度。上述内容，实质上就是热噪声的奈奎斯特定理。

（8）宇宙噪声：是指天体辐射波对接收机形成的噪声。它在整个空间的分布是不均匀的，最强的来自于银河系的中部，其强度与季节、频率等因素有关。实测表明，在20MHz~30MHz的频率范围内，它的强度与频率的3次方成正比。因此，当频率低于300MHz时，就要考虑到它的影响。实践证明，宇宙噪声也是服从高斯分布的。在一般信号的工作频率范围内，它具有较为平坦的功率谱密度，均值为零。

4.（原问题6）简述LZ编码原理，并举例说明[按照书中例5-10的条件，若输入信源符号序列U=(abbabaabbabab）]则对应的输出编码是什么？

编码原理：设信源符号集A={a1,a2,…,ak}共K个符号,设输人信源符号序列为U=(u1 ,u2,，.，un),编码是将此序列分成不同的段。分解是迭代进行的,在第i步，编码器从si-1短语后的第一个符号开始向后搜索在此之前未出现过的最短短语si,将短语si添人字典第i段。由于si是此时字典中最短的新短语，所以si在去掉最后一个符号x后所得的前缀必定是字典中之前已经出现过的。若设此前缀是在第j(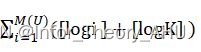i=1M(U)([logi ]+[logK] ) 。

LZ编码步骤：

（1）将信源输出序列分成各不相同的码段，尽可能取最短码段且各段不相同。

（2）将第一步分好的各码段作为字典内容，码段的序号作为字典索引。

（3）编码，新的码段是前面出现过的码段与新的信源输出的拼接。

举例（书中例5-10）：信源符号集 A={a,b}，输人信源符号序列U= (abbabaabbababb)。对输人序列进行分段，单符号a和b分别赋予段号1和2，码字分别为(0,a)和(0,b),二进制码为00和01。ba为段号3，对应的码字为(2,a)，二进制码为100。baa为段号4，对应的码字为(3,a)，二进制码为110。bb为段号5，对应的码字为(2,b)，二进制码为0101。ab为段号6，对应的码字为(1,b)，二进制码为0011。abb为段号7，对应码字为(6,b)，二进制码为1001。最后由于要编程二进制码，因此对信源符号的编码可以采用logK 个二进制数来表示，对每个段码来说，可以采用[logi ] 个二进制数表示，把相应的十进制数转换成相应长度的二进制数即可。最后得到输出的二进制码流为0001100110010100111101。