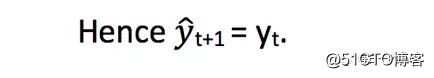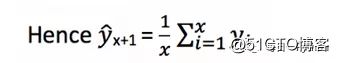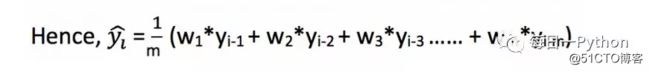python 时间序列预测 forecast,时间序列预测的7种方法（1）（Python代码实现）

本文翻译自https://www.analyticsvidhya.com/blog/2018/02/time-series-forecasting-methods/，数据集来源于https://datahack.analyticsvidhya.com/contest/practice-problem-time-series-2/。

目录表：

理解数据集和问题陈述

安装包(statsmodels)

方法1-从朴素法开始(Naive Approach)

方法2-简单平均(Simple average)

方法3-移动平均(Moving average)

方法4-一次指数平滑(Single exponential smoothing)

方法5-霍尔特线性趋势预测(Holt's linear trend method)

方法6-三次指数平滑法(Holt 's Winter seasonal method)

方法7-自回归积分滑动平均模型(ARIMA)

这篇文章先翻译到方法3-移动平均章节；

理解数据集和问题陈述

上述的数据集是关于预测JetRail通勤者数量的时间序列问题，JetRail是独角兽投资的新高速铁路服务；该数据集包含了从2012.8--2014.9的两年的数据，利用这些数据我们需要预测接下来7个月的通勤者数量；

从上述数据集下载链接下载数据后，包含train和test两个数据集，这边章 只用到了train 数据集；

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

#导入数据

df = pd.read_csv('Train.csv')

#打印头部

df.head()

#打印尾部

df.tail()

从上述的打印语句可以看出，2012-2014这两年的数据数据是按照小时的通勤数量给出的，我们需要预估将来通勤的数量；

在这篇文章中，为了解释不同的方法，数据以天为基准进行细分和聚合；

构建数据子集，时间从2012.8-2013.12

产生训练集和测试集去训练模型。从2012.8-2013.10这14个月的数据用做训练集，2013.11-2013.12这两个月的数据用做测试集；

以天为单位聚合数据

#构建数据子集

#索引11856标志着2013年结束

df = pd.read_csv('Train.csv', nrows=11856)

# 创建测试集和训练集

#索引10392标志着2013.10的结尾

train = df[0:10392]

test = df[10392:]

#以天为单位聚合数据

df.Timestamp = pd.to_datetime(df.Datetime, format='%d-%m-%Y %H:%M')

df.index = df.Timestamp

df = df.resample('D').mean()

train.Timestamp = pd.to_datetime(train.Datetime,

format='%d-%m-%Y %H:%M')

train.index = train.Timestamp

train = train.resample('D').mean()

test.Timestamp = pd.to_datetime(test.Datetime,

format='%d-%m-%Y %H:%M')

test.index = test.Timestamp

test = test.resample('D').mean()

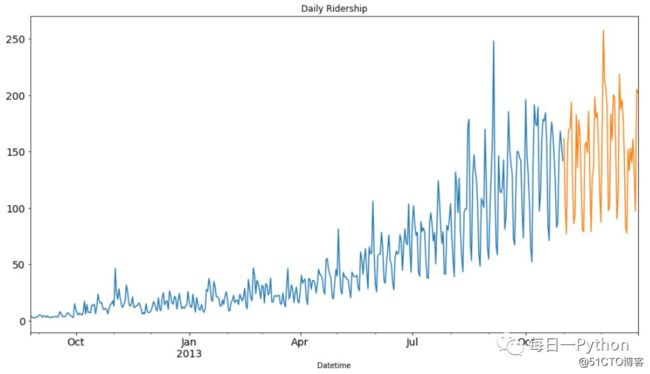
可视化数据(train和test一起)看一下在一段时间内数据是如何变化的

#绘图

train.Count.plot(figsize=(15,8),

title = 'Daily Ridership', fontsize=14)

test.Count.plot(figsize=(15,8),

title = 'Daily Ridership', fontsize=14)

plt.show()

2.安装包(statsmodels)

预测时间序列需要用到的包是statsmodels，statsmodels也许在你的的Python环境下已经存在在，但是不支持预测方法。我们需要从Git仓库中克隆下它，用源来安装，步骤如下:

1.用pip freeze 来检测statsmodels包是否存在；

2.如果存在，需要用conda remove statsmodels 移除(没装anaconda用 pip uninstall statsmodels来移除)

3.用 git clone git://github.com/statsmodels/statsmodels.git来克隆statsmodels仓库， 在克隆之前需要用git init来初始化Git

4.用 cd statsmodels 改变目录到statsmodels(先安装cpython,numpy和scipy)

5.用python setup.py build 创建安装文件

6.用python setup.py install安装

7.退出终端

8.重启终端，打开Python，执行 from statsmodels.tsa.api import ExponentialSmoothing来验证

3.方法1：从朴素法开始(Naive Approach)

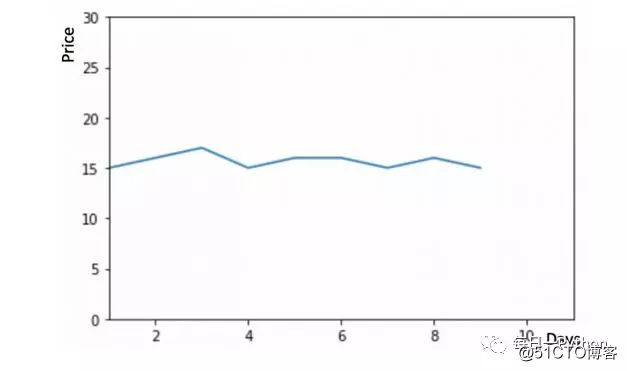
思考一下下面的图形；将Y轴看做是硬币的价格，X轴代表时间(天)

从图表我们可以推断出硬币的价格从一开始就是稳定的，很多时候我们会拥有一个在时间周期内是稳定的数据集，如果我们要预测下一天的数据的话，就可以简单的将最后的一天的值预估为下一天的值；这种假设下个期望值等于最后被观测值的预测方法被称为朴素法(Naive Method)

现在用朴素法预测一下测试集的价格：

dd = np.asarray(train.Count)

y_hat = test.copy()

#让预测数据等于测试集最后一个值

y_hat['naive'] = dd[len(dd) - 1]

plt.figure(figsize=(12,8))

plt.plot(train.index, train['Count'], label='Train')

plt.plot(test.index, test['Count'], label='Test')

plt.plot(y_hat.index, y_hat['naive'], label='Naive Forecast')

plt.legend(loc='best')

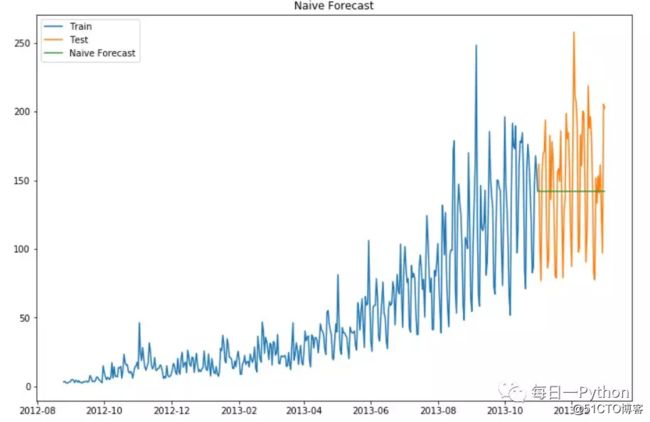
plt.title('Naive Forecast')

plt.show()

现在计算一下RMSE，检验一下模型在测试集上的准确性：

from sklearn.metrics import mean_squared_error

from math import sqrt

rms = sqrt(mean_squared_error(test.Count, y_hat.naive))

print(rms)

RMSE = 43.9164061439

我们可以从RMSE和上面的图推断，朴素法不适用于波动较大的数据，最适用于稳定的数据集，我们还可以采用不同的技巧来提升分数；现在来看另一种方法试试去提升分数

4.方法2-简单平均(Simple Average)

思考一下下面的图形；将Y轴看做是硬币的价格，X轴看作时间(天)。

从图表可以推断出，硬币的价格在小幅度地随意上升和下降，但平均值保持不变。很多时候我们会有这样一个数据集，虽然在时间周期内一直小幅度的变动，但每个时间段的平均值保持不变。在这种情况下，我们可以将下一天的价格预测为过去几天的平均值；

这种将期望值等于所有之前被观测值的平均值的方法被称为简单平均法(Simple Average technique):

我们取之前已知的所有值，计算其平均数，然后把它当做下一个值；当然这是不准确的，但多少有点接近；这种预测方法在实际情况下效果最好。

y_hat_avg = test.copy()

y_hat_avg['avg_forecast'] = train['Count'].mean()

plt.figure(figsize=(12,8))

plt.plot(train['Count'], label='Train')

plt.plot(test['Count'], label='Test')

plt.plot(y_hat_avg['avg_forecast'], label='Average Forecast')

plt.legend(loc='best')

plt.show()

现在计算RMSE来检验模型的准确性:

rms = sqrt(mean_squared_error(test.Count, y_hat_avg.avg_forecast))

print(rms)

RMSE = 109.545990803

可以看出这个模型没有提升分数，因此我们可以推断出，这个方法对在一段时间内平均数保持不变的数据作用效果好；虽然朴素法的分数比平均法的高，但不意味着朴素法在所有数据集上都比平均法效果好，我们应该一步一步地向模型移动，来判断它是否有提升我们的模型。

5.方法三-移动平均法

思考一下下面的图形；将Y轴看做是硬币的价格，X轴看作时间(天)。

从上面的图表可以推断出硬币的价格在一段时间之前上升了很多，但现在比较稳定。很多时候我们会有这样一个数据集，物体的价格会在一段时间之前陡增/陡减。为了用上面的平均法，我们必须用之前的所有数据，但是用之前的所有数据并不准确。

使用初期的价格会很大程度的影响下一时期的预测；因此作为简单平均法的改进，我们仅使用过去几个时间段的平均价格；显然，这里认为只有最近的值才是重要的。这种利用时间窗口计算平均值的预测方法被叫做移动平均法；移动平均的计算涉及到规模为n的“滑动窗口”。

使用一个简单平均模型，我们根据前面固定有限的数值"P"个数值来预测时间序列中的下一个值，因此对于所有i>p:

移动平均法实际中会非常有效，特别是选择了对于序列来说正确的P;

y_hat_avg = test.copy()

y_hat_avg['moving_avg_forecast'] = train['Count'].rolling(60).mean().iloc[-1]

plt.figure(figsize=(16,8))

plt.plot(train['Count'], label='Train')

plt.plot(test['Count'], label='Test')

plt.plot(y_hat_avg['moving_avg_forecast'],

label='Moving Average Forecast')

plt.legend(loc='best')

plt.show()

我们仅选择了最后两个月(60天)的数据，现在我们计算RMSE来检验一下模型的正确性；

rms = sqrt(mean_squared_error(test.Count,

y_hat_avg.moving_avg_forecast))

print(rms)

RMSE = 46.7284072511

可以看到对于这个数据集来说，朴素法表现优于简单平均和移动平均；

对移动平均的一个改进是加权移动平均；在上述的移动平均法中，我们将过去的N个观测值的权重看成是相等的，但是我们可能会遇到过去N个的观测值每个都以不同的方式影响预测值的情况，这种对观测值施加不同权重的方法叫做加权移动平均法；

加权移动平均法是对滑动时间窗口内值给与不同的权重的移动平均，通常情况下是最近的点最重要；它需要一个权重列表(所有值的总和为1)而不是选择一个窗口大小；

例如如果我们选择[0.40, 0.25,0.20,0.15]作为权重，那我们将最后四个值分别给与40%、25%、20%和15%的权重。