【自动驾驶】路径规划—— Dubins 曲线推导(基于向量的方法)

参考资料

• Reeds-Shepp和Dubins曲线简介
• 路径规划算法学习笔记（三）——局部路径规划（Dubins Curve）
• 自动驾驶轨迹规划之dubins曲线与reeds-shepp曲线
• Dubins Curves
• A Comprehensive, Step-by-Step Tutorial to Computing Dubin’s Paths

网上有许多dubins曲线的介绍，但我看了都迷迷糊糊的，所以我还是参考一些博客和论文自己再手推一遍，加深理解。

前言——车辆简化运动学模型

为了更好地阐述Dubins 曲线，这里我们简单地介绍一种车辆简化运动学模型。关于详细的车辆运动学模型介绍可以参考前文。

设车辆的转弯半径为：
$$R=\frac{L}{\tan {\delta }_f}$$
其中 $L$ 为前轴到后轴的长度， ${\delta }_f$ 为最大前轮转角。

而简化的运动学模型方程可以表示为：
$$\begin{array}{rl}& \dot{x}=v\cos \theta \\ & \dot{y}=v\sin \theta \\ & \dot{\theta }=\omega =\frac{v}{R}\end{array}$$
其中 $\theta$ 为偏航角，$v$为纵向速度，$\omega$为角速度。

将上述运动学方程离散化，取采样时间为$dt$，则有
$$\begin{array}{rl}& x_{\text{new }}=x_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}+v\cdot \cos (\theta )\cdot dt\\ & y_{\text{new }}=y_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}+v\cdot \sin (\theta )\cdot dt\\ & {\theta }_{\text{new }}={\theta }_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}+\frac{v}{R}\cdot dt\end{array}$$

显然，取$dt$越小，得到的离散点坐标越多。令 $\Delta s=vdt$ ，则有：
$$\begin{array}{rl}& x_{\text{new }}=x_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}+\Delta s\cdot \cos (\theta )\\ & y_{\text{new }}=y_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}+\Delta s\cdot \sin (\theta )\\ & {\theta }_{\text{new }}={\theta }_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}+\frac{\Delta s}{R}\end{array}$$

1. Dubins 曲线

1.1 基本概念

Dubins 曲线不考虑车辆后退（汽车只能朝前开），且不允许出现尖瓣。Dubins曲线是在满足曲率约束和规定的始端和末端的切线方向的条件下，连接两个二维平面（即X-Y平面）的最短路径。Dubins曲线如下图所示。

图片来源：https://blog.csdn.net/robinvista/article/details/95137143

---

Dubins曲线可以表示成3个运动基本动作的组合（即左转$L$、右转$R$、直行$S$），一般将一种组合称之为一种word。

符号	含义	绕单位圆
L	左转	逆时针
R	右转	顺时针
S	直走	直走

Dubins 给出了充分的路径集合，该集合里所包含的曲线叫做最佳路径。但是这个充分集合很小，对于每种特定终点情况下的集合中，最多只有6条可选曲线，分别表示如下：
$$\left\{\begin{array}{llllll}LRL& LSL& LSR& RLR& RSR& RSL\end{array}\right\}\text{\hspace{1em}(1)}$$

为什么是6条可选的曲线？

由于连续两次做同一种基本运动和做一次基本运动是等效的，所以 word经过排列组合后的有效种类有12个（除了上述6个还有其余6个：$SLS,SRS,SLR,SRL,RLS,LRS$）。论文又证明最短路径只在12种中的6种word中即公式(1)去选取。

Dubins 证明了，一个最优路径一定是由分段圆弧 (单位圆) 和线段组成的平滑曲线，且最多 3 部分组成。可以进一步简化表示为如下形式：

$$\begin{array}{llllllll}CCC& \to & \{& LRL& RLR& \}& & \\ CSC& \to & \{& LSL& RSR& LSR& RSL& \}\end{array}\text{\hspace{1em}(2)}$$

等式 (2) 中符号含义如下：

符号	含义
C	单位圆弧
S	一条直线段

一个word表示相应的一类路径，对于$L$和$R$，其下标表示旋转的角度；对于$S$，其下标表示行驶的直线距离。比如下图的$(R_{\alpha }{S}_d{L}_{\gamma })$ 。

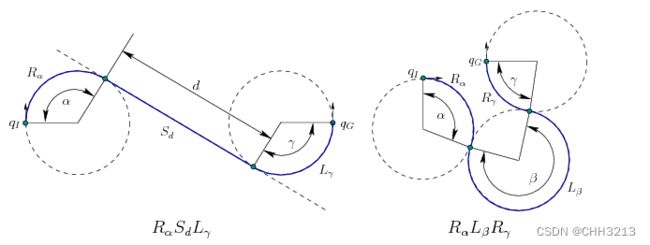
综上，Dubins曲线路径被定义为：

在最大曲率限制下，平面内两个有方向的点间的最短可行路径是$CLC$路径或$CCC$路径，或是他们的子集，其中$C$表示圆弧段，$L$表示与$C$相切的直线段。

可能的疑惑：

• 两点之间不是直线最短吗，为什么要加入圆弧？

  因为这是在带有方向的初始位置 （起始位姿点）和终止位置 （终止位姿点）间寻找最短路径，所以这是两个位姿点间的最短路径，而不是单纯的两个坐标点间的最短路径。

• 最短路径在最小半径的时候取到的前提是在无障碍的情况下

1.2 CSC轨迹

对于$CSC$轨迹来说，它包括：$RSR,LSR,RSL,和LSR$四种情况，下图是$RSR$的轨迹情况：

对于四组圆的组合：$RR,LL,RL,LR$，他们之间的切线如下图所示，其中蓝色箭头表示开始的运动方向，绿色箭头表示结束时的运动方向。

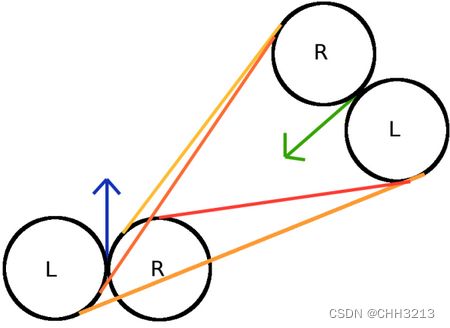
1.3 CCC轨迹

$CCC$轨迹是另一组完全不同的轨迹，包括$LRL和RLR$。它们由一个方向的转弯组成，然后朝相反的方向组成，然后再进行另一个转弯，如下图所示的RLR轨迹。

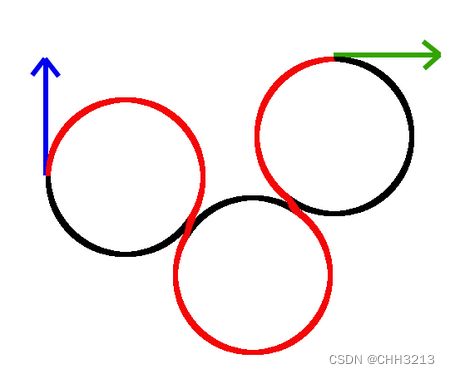
2. Dubins曲线推导计算

计算的关键

对于给定的两个圆的圆心位置，如何计算切点位置。

• 对于$CSC$类型的组合，其关键是根据起终点出发的两个圆，计算出一条切线，由于起终点的方向性，这条切线唯一。

• 对于$CCC$类型的组合，其关键是计算过渡切圆的位置。

2.1 CSC轨迹推导计算

2.1.1 已知圆心位置和半径，求切点

1. RSR和LSL

如图，$LSL$和$RSR$的示意图如下：

RSR

LSL

由于$LSL$和$RSR$的推导是完全一致的，因此以上面任意一幅图为例进行推导都行。

为了推导方便，我们这里将起点圆和终点圆的最小转弯半径分别用了两个符号表示，并且画出的起点和终点圆的大小不同，但实际上最小转弯半径是一样的。

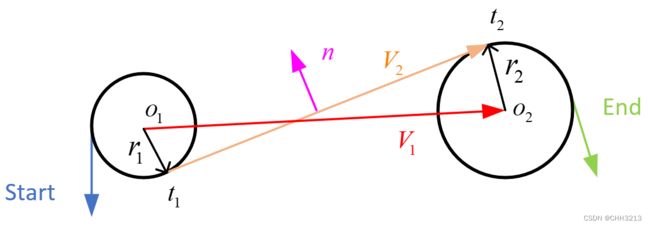
假设两个最小转弯半径构成的圆，半径大小分别为$r_1$和$r_2$，圆心分别为$o_1$和$o_2$，两个切点分别为$t_1$和$t_2$。两个圆心间的连线构成向量$V_1$，两个切点之间的连线（即切线）构成向量$V_2$，切线的单位法向量为$n$，他们的方向分别如图所示。

显然，单位法向量$n$与两圆心到切点的连线（即$o_1{t}_1$，$o_2{t}_2$）是平行的。

我们需要求解的问题是：已知圆心位置和半径的前提下，求切点。

根据已知条件，$V_2\perp n$，显然有
$$V_2\cdot n=0$$

在四边形$o_1{o}_2{t}_2{t}_1$中，根据向量的几何关系（注意向量定义的方向）有

$$V_2=-o_1{t}_1+V_1+o_2{t}_2\text{\hspace{1em}(3)}$$

由图几何关系可知
$$\begin{gathered} o_1{t}_1=r_1\cdot n \\ {o}_2{t}_2=r_2\cdot n\text{\hspace{1em}(4)} \end{gathered}$$

所以
$$V_2=V_1+(r_2-r_1)\cdot n\text{\hspace{1em}(5)}$$

等式(5)两边右乘单位法向量$n$，得
$$\begin{array}{rl}{V}_2\cdot n& =(V_1+(r_2-r_1)\cdot n)\cdot n\\ & \Downarrow \\ 0& =(V_1+(r_2-r_1)\cdot n)\cdot n\\ & \Downarrow \\ 0& =V_1\cdot n+r_2-r_1\\ & \Downarrow \\ V_1\cdot n& =r_1-r_2\end{array}\text{\hspace{1em}(6)}$$

进一步地，记$V_1$模长为$D$，将单位化后的$V_1$记为$\frac{V_1}{D}=V_{1n}$，将等式(6)两边同除以$D$，由于$V_{1n}$和$n$都是单位向量，故得
$$\begin{array}{rl}\frac{V_1\cdot n}{D}& =\frac{r_1-r_2}{D}\\ & \Downarrow \\ V_{1n}\cdot n& =\frac{r_1-r_2}{D}\\ & \Downarrow \\ V_{1n}\cdot n& =c\\ & \Downarrow \\ V_{1n}\cdot n& =||V_{1n}||\cdot ||n||\cdot \cos \theta =\cos \theta =c\end{array}\text{\hspace{1em}(7)}$$

式中$c=\frac{r_1-r_2}{D}=\cos \theta$，$\theta$是$V_1$和$n$的夹角，显然$\sin \theta =\sqrt{1-c^2}$。

假设$V_{1n}=(v_{1nx},v_{1ny})$，$n=(n_x,n_y)$，将之代入公式(7)，化简后可求出$n$：
$$\{\begin{array}{l}{n}_x=v_{1nx}\ast c-v_{1ny}\ast \sqrt{1-c^2}\\ n_y=v_{1ny}\ast c+v_{1nx}\ast \sqrt{1-c^2}\end{array}\text{\hspace{1em}(8-1)}$$

因为向量$V_{1n}$旋转角度$\theta$就得到了向量$n$，所以根据向量旋转的数学计算也可得出。

计算出$n$之后，就可以很方便的计算出两个切点：从圆心$o_1$出发，沿着向量$n$的方向，走过半径$r_1$的距离即为切点$t_1$；$t_2$同理。

即起点圆的切点坐标$(x_{t1},y_{t1})$为：
$$\begin{gathered} x_{t1}=x_{o1}+r_1\ast n_x \\ {y}_{t1}=y_{o1}+r_1\ast n_y \\ \text{\hspace{1em}(8-2)} \end{gathered}$$
终点圆的切点坐标$(x_{t2},y_{t2})$为：
$$\begin{gathered} x_{t2}=x_{o2}+r_2\ast n_x \\ {y}_{t2}=y_{o2}+r_2\ast n_y \\ \text{\hspace{1em}(8-3)} \end{gathered}$$

2. RSL和LSR

$RSL$和$LSR$的推导过程与上一小节完全类似。

RSL

LSR

由于 $RSL$和$LSR$的推导是完全一致的，因此以上面任意一幅图为例进行推导。在四边形$o_1{t}_1{t}_2{o}_2$中，根据向量的几何关系有

$$V_2=-o_1{t}_1+V_1+o_2{t}_2$$

由图中几何关系可知
$$\begin{gathered} o_1{t}_1=-r_1\cdot n \\ {o}_2{t}_2=r_2\cdot n \end{gathered}$$

所以
$$V_2=V_1+(r_2+r_1)\cdot n\text{\hspace{1em}(9)}$$

等式(9)两边右乘$n$，得
$$\begin{array}{rl}{V}_2\cdot n& =(V_1+(r_2+r_1)\cdot n)\cdot n\\ & \Downarrow \\ 0& =(V_1+(r_2+r_1)\cdot n)\cdot n\\ & \Downarrow \\ 0& =V_1\cdot n+r_2+r_1\\ & \Downarrow \\ V_1\cdot n& =-r_1-r_2\end{array}\text{\hspace{1em}(10)}$$

进一步地，记$V_1$模长为$D$，将单位化后的$V_1$记为$\frac{V_1}{D}=V_{1n}$，将等式(10)两边同除以$D$，由于$V_{1n}$和$n$都是单位向量，故得
$$\begin{array}{rl}\frac{V_1\cdot n}{D}& =\frac{-r_1-r_2}{D}\\ & \Downarrow \\ V_{1n}\cdot n& =\frac{-r_1-r_2}{D}\\ & \Downarrow \\ V_{1n}\cdot n& =c\\ & \Downarrow \\ V_{1n}\cdot n& =||V_{1n}||\cdot ||n||\cdot \cos \theta =\cos \theta =c\end{array}\text{\hspace{1em}(11)}$$

式中$c=\frac{-r_1-r_2}{D}<0$，$\theta$是$V_1$和$n$的夹角，显然$\sin \theta =\sqrt{1-c^2}$，且$\theta$大于90°。

假设$V_{1n}=(v_{1nx},v_{1ny})$，$n=(n_x,n_y)$，将之代入公式(11)，化简后可求出$n$：
$$\{\begin{array}{l}{n}_x=v_{1nx}\ast c+v_{1ny}\ast \sqrt{1-c^2}\\ n_y=v_{1ny}\ast c-v_{1nx}\ast \sqrt{1-c^2}\end{array}\text{\hspace{1em}(12-1)}$$

因为向量$V_{1n}$旋转角度$\theta$就得到了向量$n$，所以根据向量旋转的数学计算也可得出。

计算出$n$之后，就可以很方便的计算出两个切点：从圆心$o_1$出发，沿着向量$o_1{t}_1$的方向(即$n$的反方向)，走过半径$r_1$的距离即为切点$t_1$；$t_2$同理。

即起点圆的切点坐标$(x_{t1},y_{t1})$为：
$$\begin{gathered} x_{t1}=x_{o1}-r_1\ast n_x \\ {y}_{t1}=y_{o1}-r_1\ast n_y \\ \text{\hspace{1em}(12-2)} \end{gathered}$$
终点圆的切点坐标$(x_{t2},y_{t2})$为：
$$\begin{gathered} x_{t2}=x_{o2}+r_2\ast n_x \\ {y}_{t2}=y_{o2}+r_2\ast n_y \\ \text{\hspace{1em}(12-3)} \end{gathered}$$

2.1.2 已知起点终点位姿，求圆心坐标

假设已知起点 $s=\left(x_1,y_1,{\theta }_1\right)$ 和终点 $g=\left(x_2,y_2,{\theta }_2\right)$ ， ${\theta }_1,{\theta }_2$表示航向角。然后我们计算起点圆和终点圆的圆心。

(1) 当车辆右转时

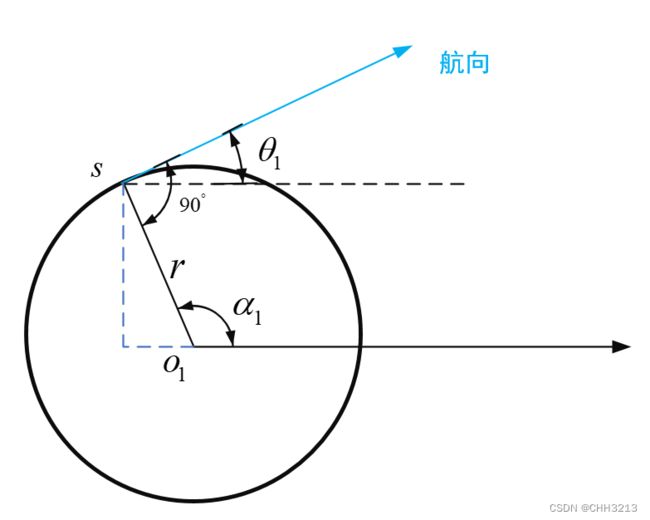
如上图所示，根据几何关系，圆心$o_1$的坐标$(x_{o1},y_{o1})$可以表示为

$$\{\begin{array}{l}{x}_{o1}=x_1+r_1\ast \cos (180°-{\alpha }_1)\\ y_{o1}=y_1-r_1\ast sin(180°-{\alpha }_1)\end{array}\text{\hspace{1em}(13)}$$

而${\alpha }_1$和${\theta }_1$的关系为
$$90°-{\theta }_1+{\alpha }_1=180°$$
即
$${\alpha }_1=90°+{\theta }_1\text{\hspace{1em}(14)}$$

将公式(14)代入公式(13)，使用三角函数公式化简后得到起点圆的圆心为:
$$o_1=\left(x_1+r_1\ast \sin {\theta }_1,y_1-r_1\ast \cos {\theta }_1\right)\text{\hspace{1em}(15)}$$
同理可得，终点圆的圆心为:
$$o_2=\left(x_2+r_2\ast \sin {\theta }_2,y_2-r_2\ast \cos {\theta }_2\right)\text{\hspace{1em}(16)}$$

(2) 当车辆左转时

类似的分析，如上图所示，根据几何关系，圆心$o_1$的坐标$(x_{o1},y_{o1})$可以表示为

$$\{\begin{array}{l}{x}_{o1}=x_1+r_1\ast \cos (180°-{\alpha }_1)\\ y_{o1}=y_1-r_1\ast sin(180°-{\alpha }_1)\end{array}\text{\hspace{1em}(17)}$$

而${\alpha }_1$和${\theta }_1$的关系为
$$360°-90°-{\theta }_1+{\alpha }_1=180°$$
即
$${\theta }_1=90°+{\alpha }_1\text{\hspace{1em}(18)}$$

将公式(18)代入公式(17)，化简后得到起点圆的圆心为:
$$o_1=\left(x_1-r_1\ast \sin {\theta }_1,y_1+r_1\ast \cos {\theta }_1\right)\text{\hspace{1em}(19)}$$
同理可得，终点圆的圆心为:
$$o_2=\left(x_2-r_2\ast \sin {\theta }_2,y_2+r_2\ast \cos {\theta }_2\right)\text{\hspace{1em}(20)}$$

2.1.3 求行驶轨迹

$CSC$类型曲线轨迹求解流程：

首先得到起点圆和终点圆的圆心，然后计算出两个圆的切点，计算出切点后，车辆便可以沿着最小转弯半径构成的圆周行驶到第一个圆的切点，然后直行到第二个圆的切点，再沿着最小转弯半径构成的圆周行驶到目的地。

通过2.1.2小节计算得到起点和终点圆的圆心之后，利用2.1.1小节的切点计算方法，便可以得到切点。然后就可以得到车辆的行驶轨迹，该轨迹分为三段：start到切点$t_1$的圆周弧；$t_1$和$t_2$的直线距离；$t_2$到End的圆周弧。至此我们便得到了$CSC$的行驶曲线。

2.1.4 python代码实现

下面参考资料2的matlab程序，写了python代码，并没有考虑最优路径。

import numpy as np
import matplotlib.pyplot as plt

"""Dubins Curve CSC型

"""

#目标定义
#定义起终点[x y dir]
S = np.array([1, 1, 7 * np.pi / 4])
G = np.array([6, 8, 3 * np.pi / 4])
#定义转弯半径
ri = 1
rg = 1

#组合

i = -1 # 1:右转，-1：左转 ---起点圆
j = 1 # 1:右转，-1：左转 ---终点圆
k = i*j # 1:RSR/LSL, -1: RSL/LSR

"""计算首尾圆心坐标"""
xi = S[0] + ri * i * np.sin(S[2])
yi = S[1] - ri * i * np.cos(S[2])
xg = G[0] + rg * j * np.sin(G[2])
yg = G[1] - rg * j * np.cos(G[2])

"""计算法向量"""
#起终点圆圆心之间的向量V1=[v1x,v1y]
v1x = xg - xi
v1y = yg - yi
# V1模长
D = np.sqrt(v1x * v1x + v1y * v1y)
# 单位化
v1x = v1x / D
v1y = v1y / D
#计算法向量n
c = (k * ri - rg) / D
nx = v1x * c - j * v1y * np.sqrt(1 - c * c)
ny = v1y * c + j * v1x * np.sqrt(1 - c * c)



"""计算起终点圆的切点"""
xit = xi + k * ri * nx
yit = yi + k * ri * ny
xgt = xg + rg * nx
ygt = yg + rg * ny

# print(xgt-xg,ygt-yg)
# print(nx,ny)

"""绘图"""
# # 画起终点的初始方向
xiDir = np.array([S[0], S[0]+ri*np.cos(S[2])])
yiDir = np.array([S[1], S[1]+ri*np.sin(S[2])])
xgDir = np.array([G[0], G[0]+rg*np.cos(G[2])])
ygDir = np.array([G[1], G[1]+rg*np.sin(G[2])])


#切点连线即切线
tangent_x = np.array([xit, xgt])
tangent_y = np.array([yit, ygt])

# 画出首尾圆
t = np.arange(0, 2 * np.pi+0.01, 0.01)

# t = np.arange(S[2] - np.pi / 2, 3 * np.pi / 2 - np.arctan(ny / nx)+0.01, 0.01)
circle_xi = xi + ri * np.cos(t)
circle_yi = yi + ri * np.sin(t)

# t = np.arange(- np.pi / 2 - np.arctan(ny / nx),G[2] - np.pi / 2+0.01,0.01)
circle_xg = xg + rg * np.cos(t)
circle_yg = yg + rg * np.sin(t)


plt.plot(S[0], S[1], 'go', G[0], G[1], 'go', xiDir, yiDir, '-g', xgDir, ygDir, '-g', xi, yi,
         'k*', xg, yg, 'k*', circle_xi, circle_yi, '-r', circle_xg, circle_yg, '-r', [xi,xit], [yi,yit], '-b', [xg,xgt],[yg,ygt], '-b', tangent_x, tangent_y, '-r')

plt.axis('equal')
plt.show()

这是$LSR$曲线的效果：

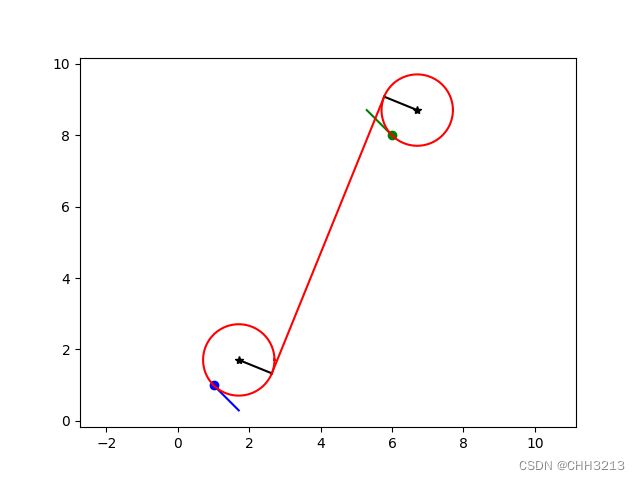
2.2 CCC轨迹推导计算

RLR

LRL

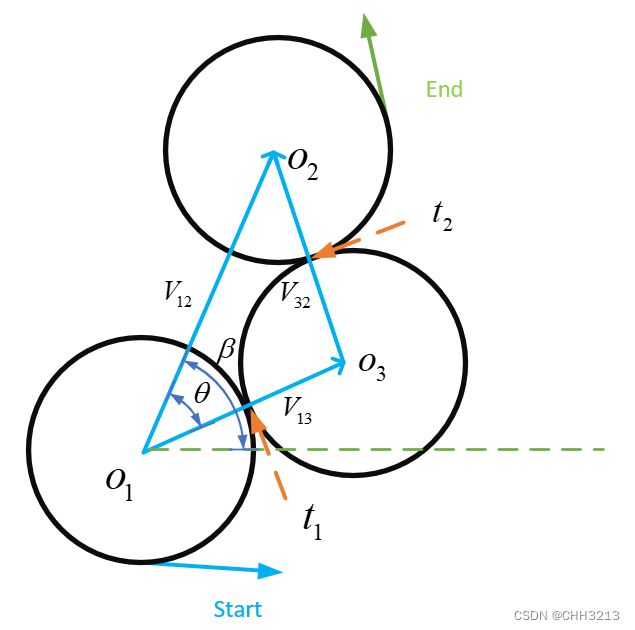
2.2.2 推导过程

$CCC$轨迹的推导比较纯几何，假设圆心$o_1,o_2$和三个圆的半径已知，则表明三角形$\Delta o_1{o}_3{o}_2$的边长均已知，首先先求出$V_{12}$与水平方向的夹角$\beta$，然后通过余弦定理可以求出$\theta$，继而根据三角关系，用$o_1$坐标计算$o_3$坐标。

我们假设$o_1,o_2,o_3$的半径分别为$r_1,r_2,r_{mid}$。

根据数学关系，可得到:
$$\{\begin{array}{l}\left|\overline{o_1{o}_2}\right|=D=\sqrt{{\left(x_{o2}-x_{o1}\right)}^2+{\left(y_{o2}-y_{o1}\right)}^2}\\ \left|\overline{o_1{o}_3}\right|=r_1+r_{mid}\\ \left|\overline{o_2{o}_3}\right|=r_2+r_{mid}\end{array}\text{\hspace{1em}(21)}$$

根据余弦定理有：
$$\theta ={\cos }^{-1}\left(\frac{{\left|\overline{o_1{o}_3}\right|}^2+{\left|\overline{o_1{o}_2}\right|}^2-{\left|\overline{o_2{o}_3}\right|}^2}{2\cdot \left|\overline{o_1{o}_3}\right|\cdot \left|\overline{o_1{o}_2}\right|}\right)\text{\hspace{1em}(22)}$$

最终可得到:
$$o_3=\left(x_1+\left|\overline{o_1{o}_3}\right|\cdot \cos (\beta -\theta ),y_1+\left|\overline{o_1{o}_3}\right|\cdot \sin (\beta -\theta )\right)\text{\hspace{1em}(23)}$$

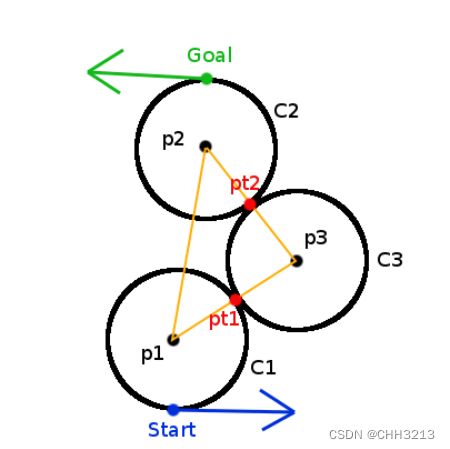
解出$o_3$坐标后,只需从$o_1$出发，沿$V_{13}$（$V_{13}=o_3-o_1$，其他同理）走过半径$r_1$的距离，即可得到第一个切点，同理沿$V_{32}$方向，可得第二个切点位置。

定义向量 $V_{13}=o_3-o_1$ ，则切点$t_1$的坐标为 。
$$t_1=o_1+\frac{V_{13}}{\Vert V_{13}\Vert }\ast r_1\text{\hspace{1em}(24)}$$
按照同样的过程可以计算得到 $t_2$ 。然后就可以得到起点到切点$t_1$的圆周弧；$t_1$和$t_2$之间的圆周弧；$t_2$到终点的圆周弧的三段轨迹组成的行驶曲线。

---

说明

---

一般地，对于最优情况来说，我们假设$o_1,o_2,o_3$具有最小转弯半径$r_{min}$。

根据数学关系，可得到:
$$\{\begin{array}{l}\left|\overline{o_1{o}_2}\right|=D=\sqrt{{\left(x_{o2}-x_{o1}\right)}^2+{\left(y_{o2}-y_{o1}\right)}^2}\\ \left|\overline{o_1{o}_3}\right|=2r_{\min }\\ \left|\overline{o_2{o}_3}\right|=2r_{\min }\end{array}\text{\hspace{1em}(25)}$$
此时三角形$\Delta o_1{o}_3{o}_2$为等腰三角形，根据余弦定理，有:
$$\theta ={\cos }^{-1}\left(\frac{\frac{D}{2}}{2r_{\min }}\right)={\cos }^{-1}\left(\frac{D}{4r_{\min }}\right)\text{\hspace{1em}(26)}$$
最终可得到:
$$o_3=\left(x_1+2r_{\min }\cos (\beta -\theta ),y_1+2r_{\min }\sin (\beta -\theta )\right)\text{\hspace{1em}(27)}$$

参考资料A Comprehensive, Step-by-Step Tutorial to Computing Dubin’s Paths 中的这一段没理解，先放在这，有知道的朋友们欢迎帮忙解释一下。

---

2.2.4 python代码实现

下面参考资料2的matlab程序，写了python代码，并没有考虑最优路径。

import numpy as np
import matplotlib.pyplot as plt


"""
Dubins Curve CCC型
"""


#目标定义
#定义起终点[x y psi]
S = np.array([1, 1, 7 * np.pi / 4])
G = np.array([4, 5, 3 * np.pi / 4])
#定义转弯半径
ri = 1
rg = 1
rmid = 1


i = -1 # 1:右转，-1：左转


"""计算首尾圆心坐标及其连线向量V12"""
xi = S[0] + ri * i * np.sin(S[2])
yi = S[1] - ri * i * np.cos(S[2])
xg = G[0] + rg * i * np.sin(G[2])
yg = G[1] - rg * i * np.cos(G[2])

V12 = np.array([xg - xi,yg - yi])
angleV12 = np.arctan(V12[1] / V12[0])

"""计算中间圆坐标及三圆心连线向量V13、V32"""
d12 = np.sqrt((xg - xi) ** 2 + (yg - yi) ** 2)
rmid = np.max(np.array([rmid, (d12 - ri - rg) * 0.5]))
d13 = ri + rmid
d32 = rmid + rg
angleP213 = np.arccos((d12 ** 2 + d13 ** 2 - d32 ** 2) / (2 * d12 * d13)) # 余弦定理
xmid = xi + d13 * np.cos(angleV12 - angleP213)
ymid = yi + d13 * np.sin(angleV12 - angleP213)
V13 = np.array([xmid - xi,ymid - yi])
V32 = np.array([xg - xmid,yg - ymid])

Vn13 = V13 / d13  # 归一化
Vn32 = V32 / d32
"""计算切点坐标"""
xt1 = xi + ri * Vn13[0]
yt1 = yi + ri * Vn13[1]
xt2 = xmid + rmid * Vn32[0]
yt2 = ymid + rmid * Vn32[1]

"""绘图"""
# # 画起终点的初始方向
xiDir = np.array([S[0], S[0]+ri*np.cos(S[2])])
yiDir = np.array([S[1], S[1]+ri*np.sin(S[2])])
xgDir = np.array([G[0], G[0]+rg*np.cos(G[2])])
ygDir = np.array([G[1], G[1]+rg*np.sin(G[2])])

# 画出首尾圆
t = np.arange(0, 2 * np.pi+0.01, 0.01)

circle_xi = xi + ri * np.cos(t)
circle_yi = yi + ri * np.sin(t)

circle_xg = xg + rg * np.cos(t)
circle_yg = yg + rg * np.sin(t)

circle_xmid = xmid + rmid * np.cos(t)
circle_ymid = ymid + rmid * np.sin(t)

#绘图
plt.plot(S[0],S[1],'go',G[0],G[1],'go',xiDir,yiDir,'-g',xgDir,ygDir,'-g',xi,yi,'k*',xg,yg,'k*',xmid,ymid,'k*',xt1,yt1,'bo',xt2,yt2,'bo',circle_xi,circle_yi,'-r',circle_xg,circle_yg,'-r',circle_xmid,circle_ymid,'-r')
plt.axis('equal')
plt.show()

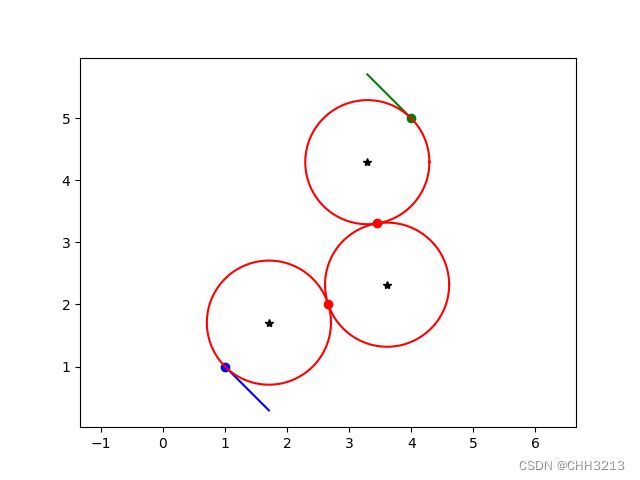
这是$LRL$曲线的实现效果：

3. 后记

• Dubins曲线是开环的，考虑到实际车辆行驶中的不确定性， Dubins还存在动态性的问题。
• Dubins曲线能够用于RRT等路径规划算法中，在原始RRT中，树枝的生长是直线生长(找到最近点，建立直线连接)，对于汽车来说，不可能一直都能实现沿直线树枝行驶，因此在新节点和整棵随机树的关联上，可以选择使用Dubins曲线，使得各节点之间有一个连续、光滑、满足车辆运动学的连接。
• Dubins曲线是不对称的，从A点到B点的最短距离，并不一定等于B点到A点的最短距离。相对的，Reeds Shepp曲线是对称的。