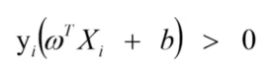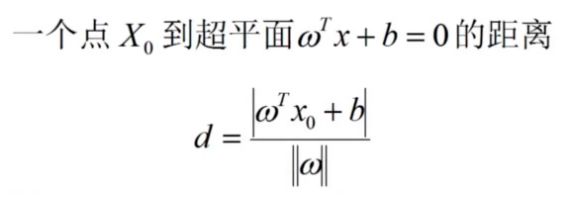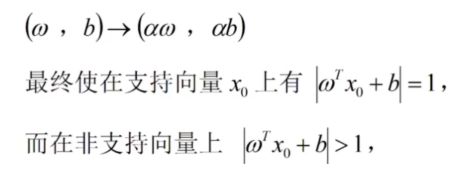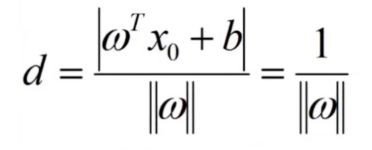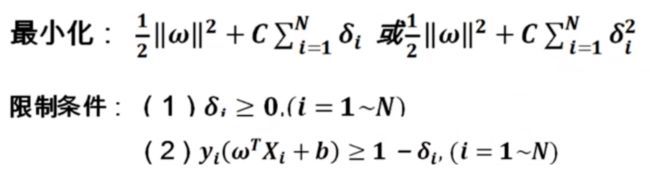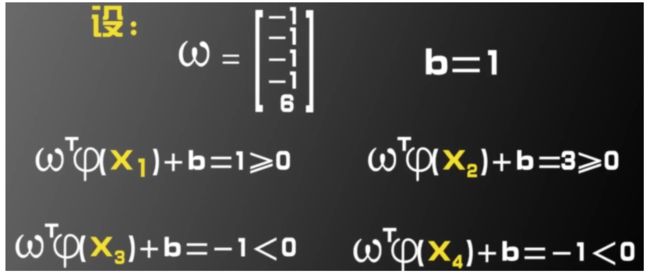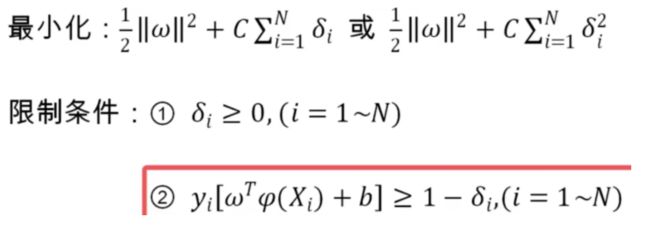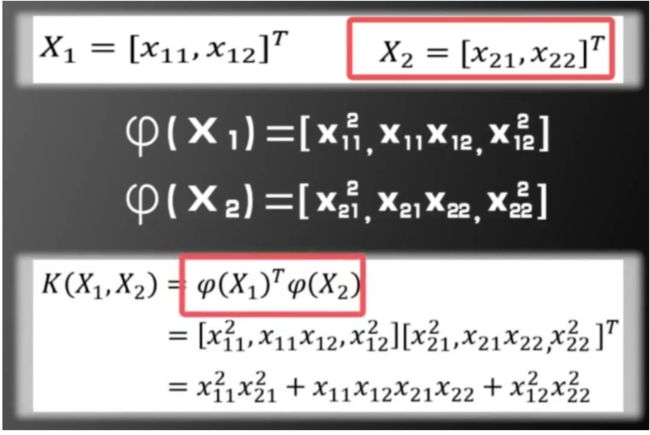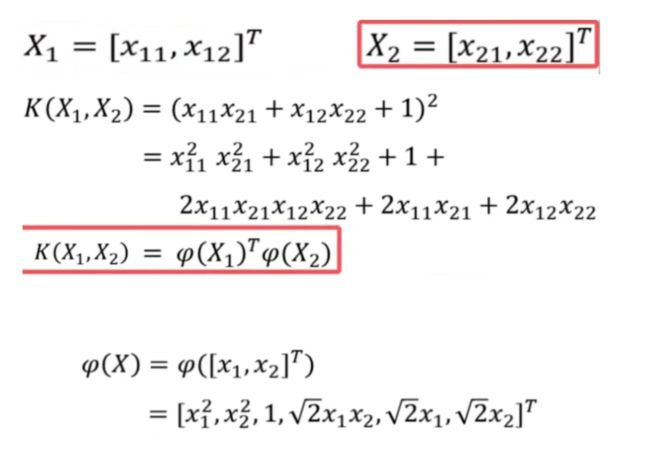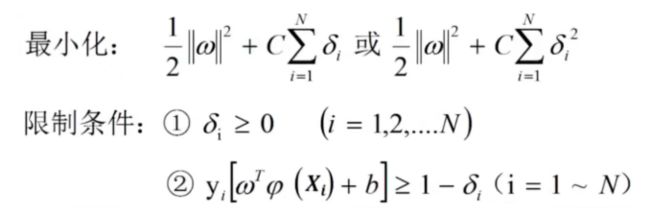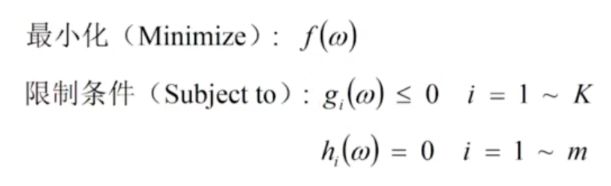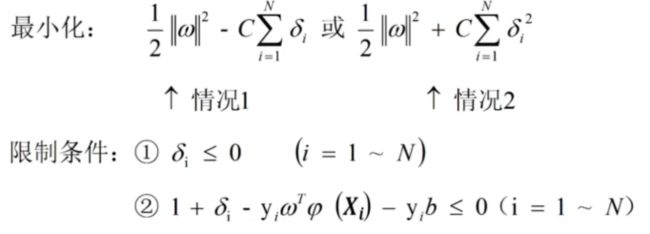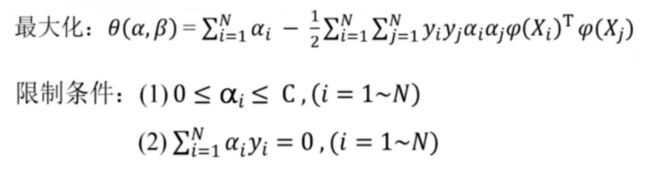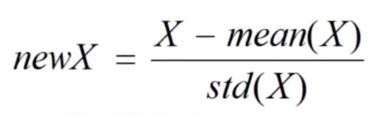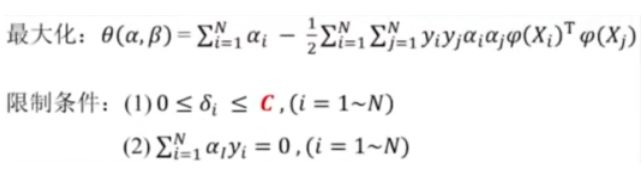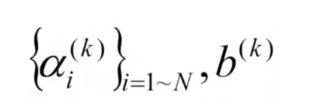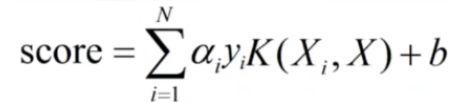【一起来啃西瓜书】——支持向量机

目录

​1.线性可分定义

2.问题描述

3.优化问题

4.线性不可分

5.低维到高维的映射

6.核函数（kernal Function）

7.原问题和对偶问题

8.支持向量机原问题转换为对偶问题

9.算法总体流程

10.SVM应用——国际象棋兵王问题

1）规则介绍

2）参数设置

3）程序设计

4）性能度量

11.SVM处理多类问题

---

​1.线性可分定义

算法创始人：Vladimir Vapnik

线性可分：Linear Separable

二维

存在一条直线将⭕和×分开

线性不可分：Nonlinear Separable

不存在一条直线将⭕和×分开

三维

    

特征空间维度>=四维时，超平面肉眼观察不到，需借助数学模型。

2.问题描述

或

用数学严格定义训练样本以及他们的标签。

假设：我们有N个训练样本和他们的标签

用数学严格的定义线性可分：

一个训练样本集{(xi,yi),...,(xn,yn)},在i=1~N线性可分，是指存在(w1,w2,b)使得对i=1~N,有：

用向量形式来定义线性可分：

如果yi=+1或-1，可归纳成一个公式：

3.优化问题

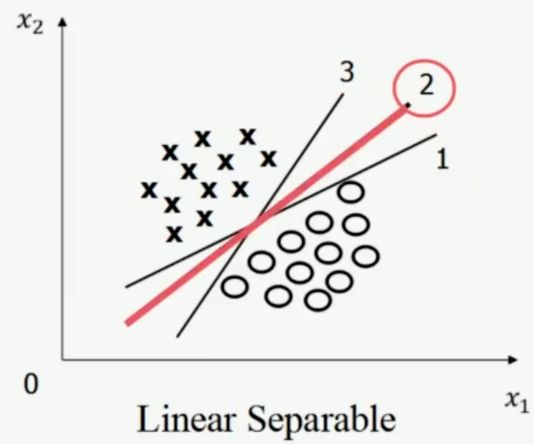
2号线是怎么画出来的？

支持向量机寻找的最优分类直线应满足——基于2维空间：

（1）该直线分开了两类；

（2）该直线最大化间隔（margin）；

（3）该直线处于间隔的中间，到所有支持向量距离相等。

支持向量机优化问题：

假定训练样本集是线性可分的，支持向量机需要寻找的是最大化间隔（margin）的超平面。

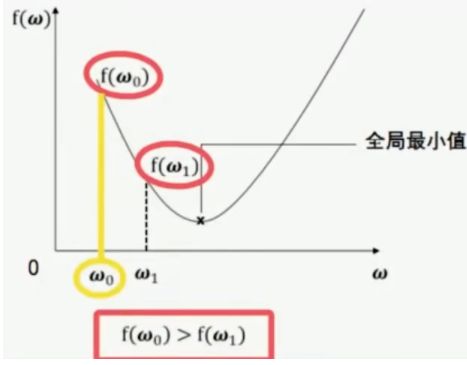
属于凸优化问题中的二次规划（目标函数是二次项&限制条件是一次项），要么无解，要么只有唯一的最小值（唯一一个全局极值）。

事实：

事实1：

事实2：

点到超平面的距离公式：

证明：

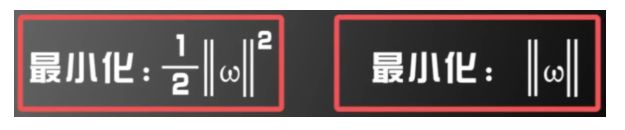
最大化支持向量到超平面的距离等价于最小化||w||

优化问题定义为：（以便后续求导方便）

4.线性不可分

用上述线性可分限制条件，对于线性不可分问题则无解。

对于线性不可分情况，需适当放松限制条件。

改造后的支持向量机优化版本：

比例因子C是人为设定的，人为事先设定的参数叫做算法的超参数（Hyper parameter），不断变化C的值，同时测试算法的识别率，选取超参数C。支持向量机是超参数很少的算法模型。

问题出在哪里？

我们假设分开两类的函数是线性的。

线性模型的表现力是不够的。

扩大可选的函数范围。

5.低维到高维的映射

SVM在扩大可选的函数范围上面独树一帜。

特征空间由低维映射到高维，用线性超平面对数据进行分类。

考察如图的异或问题：

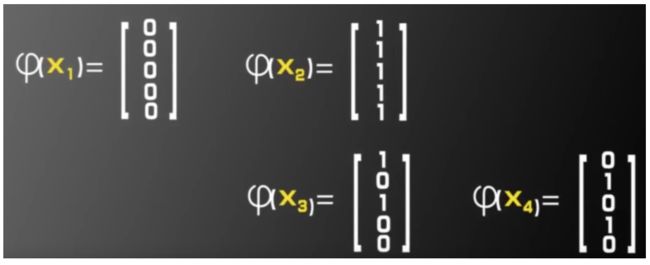
本身是线性不可分，可构造一个二维到五维的映射

求解：

从二维到五维映射变化后，线性不可分数据集变成了线性可分。

结论

在一个M维空间上随机取N个训练样本，随机的对每个训练样本赋予标签+1或-1。

假设：这些训练样本线性可分的概率为P(M)，当M趋于无穷大时，P(M)=1

特征空间的维度M增加，待估计参数（w,b）的维度也随之增加，算法模型的自由度也增加。

将训练样本由低维映射到高维，将增大线性可分的概率。

SVM的优化问题

6.核函数（kernal Function）

已知映射求核函数

假设：

假设有两个二维向量：

已知核函数求映射

假设：

核函数K和映射是一一对应的关系

核函数的形式不能随意的取，满足一定的条件

虽然无法知道映射函数的具体形式，但是知道，进而知道测试样本所属类别。

7.原问题和对偶问题

原问题与对偶问题的定义

原问题：

该原问题的对偶问题：

定理一：

定理二（强对偶定理）：

8.支持向量机原问题转换为对偶问题

SVM的优化问题

原问题

变换后的SVM优化问题

变换后两个限制条件都是线性的，目标函数是凸的，满足强对偶定理。

将对偶问题写成如下的形式：

令导数为0，可得：

将SVM的原问题化为对偶问题：

9.算法总体流程

SVM训练核测试的流程

训练过程：

测试过程：

考察测试数据X，预测它的列别y。

10.SVM应用——国际象棋兵王问题

1）规则介绍

兵：第一次向前可以走一格或两格，以后每次只能向前走一格，不能后退。

王：王被将死即告负。每次只能走一格。

兵王问题：黑方只剩一个王，白方剩一个兵一个王。

两种可能：

（1）白方将死黑方，获胜。

（2）和棋。

这两种可能视三个棋子在棋盘的位置而确定。

规则介绍：

（1）兵的升变：兵走至对方底线，可以升变为除王以外的任意一子。

（2）逼和：一方的王未被将军，但移动到任意地方都会被对方将死，则此时是和棋。

2）参数设置

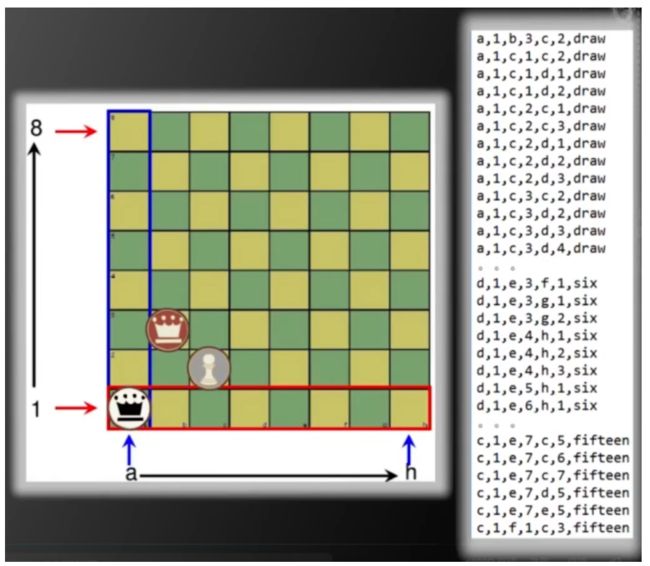
UCI MACHINE LEARNING数据集的krkopt.data

draw：和局

six：五步被将死

用SVM解兵王问题

和棋（draw） yi=+1

其他（ONE-FIFTEEN） yi=-1

总样本数：28056

正样本：2796

负样本：25260

用SVM程序进行训练：LIBSVM工具包；下载地址http://www.csie.ntu.edu.tw/~cjlin/libsvm

3）程序设计

第一步：对数据的预处理

总样本数为：28056，其中正样本2796，负样本25260

随机取5000个样本训练，其余测试。

对训练样本归一化

在训练样本上，求出每个维度的均值和方差，在训练和测试样本上同时归一化。

第二步：设置SVM的各种参数：

（1）SVM类型

目标函数

（2）核函数

线性内核只具有理论的意义，没有使用的价值。

Rbf是实际编程应用中最常用的核函数。

（3）C值

原问题的C值：

对偶问题的C值：

（4）gamma值

第三步：交叉验证

识别率怎么求：可以通过交叉验证求均值，一般用5-fold cross validation

得出结果

支持向量一般最多占20%-30%，如果支持向量数比较多，一般来说训练的不够理想

支持向量比较高的情况一般以下：

1.参数选择不好，训练的不够好

2.数据本身没有规律

3.SVM算法没有办法找到数据的规律

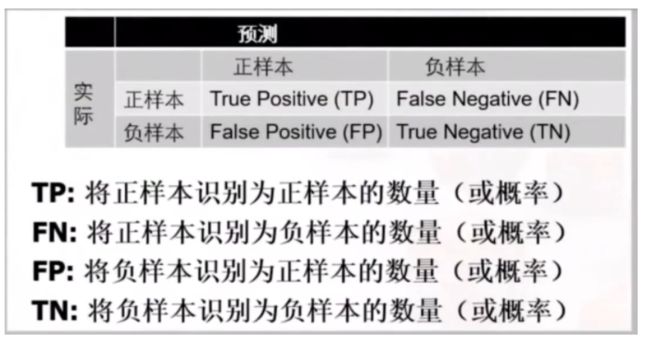
4）性能度量

混淆矩阵

兵王问题在测试样本上的混淆矩阵

ROC曲线

AUC（Area under curve）

AUC越大，系统性能越好。

等错误率ERR（equal error rate）

等错误率越小，系统性能越好。

11.SVM处理多类问题

SVM处理多类问题的方法

SVM有三种方式处理多类问题，即类别大于2的问题：

（1）改造优化的目标函数核限制条件，使其能处理多类；

（2）一类 VS 其他类；

（3）一类 VS 另一类。

SVM天生适合两类问题分割方法，SVM改造一般用的不多，效果也较一般

1类 VS k-1类 ：

假设总共有K类，我们需要构造K个SVM模型。

（1）类别1 VS 类别2，3，4，... K

（2）类别2 VS 类别1，3，4，... K

（3）类别3 VS 类别1，2，4，... K

.........................

（K）类别K VS 类别1，2，3，... K-1

假设每个优化问题，左边单一类别的标签为+1，右边K-1个类别的标签为-1。

K个组合：

对于一个测试样本X，我们判断其类别为：

1类 VS 另一类：

假设有三类，那么我们就构建三个SVM分类器。

（1）类别1 VS 类别2

（1）类别1 VS 类别3

（1）类别2 VS 类别3

投票机制：

可能存在两种类别结果一致。

类别分数：

（1）假设SVM1、SVM2、SVM3分数；

（2）计算三个SVM对类别1、类别2、类别3的分数和；

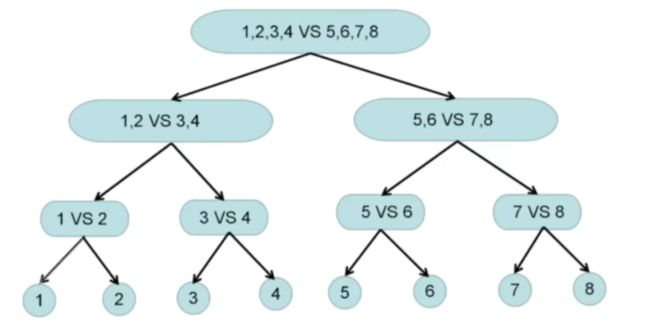
（3）取分数和最大的SVM，即为最后的分类结果

一般综合上述两种方法，如处理8分类问题，构建了7个分类器：