搭建解决三好学生成绩问题的神经网络04------简化神经网络模型

前言：

我们在https://blog.csdn.net/qq_39432161/article/details/100859092 中构建的三好学生神经网络模型更多的是从一般的思维方法来设计的，这与神经网络通常设计中的思路并不一致。现在我们对这个模型进行优化，让它的逻辑更加清晰、运行更加高效。

基本概念：

1. 张量、向量、矩阵的相关概念请看https://blog.csdn.net/qq_39432161/article/details/115307655

 

张量在tensorflow使用:

我们先看一段代码：从三好学生神经网络模型截取的部分代码，添加了几个print语句以便查看变量的取值。

# Author:北京
# QQ:838262020
# time:2021/3/30

# 导入TensorFlow包
import tensorflow as tf

# 定义三个占位符，数据类型为浮点型
x1 = tf.placeholder(dtype=tf.float32)
x2 = tf.placeholder(dtype=tf.float32)
x3 = tf.placeholder(dtype=tf.float32)
yTrain = tf.placeholder(dtype=tf.float32)
print('x1: %s' % x1)

# 定义三个可变参数，数据类型为浮点型
w1 = tf.Variable(0.1, dtype=tf.float32)
w2 = tf.Variable(0.1, dtype=tf.float32)
w3 = tf.Variable(0.1, dtype=tf.float32)
print('w1: %s' % w1)
n1 = w1 * x1
n2 = w2 * x2
n3 = w3 * x3
print('n1: %s' % n1)
y = n1 + n2 + n3
print('y: %s' % y)

运行结果：

x1: Tensor("Placeholder:0", dtype=float32)
w1: 
n1: Tensor("mul:0", dtype=float32)
y: Tensor("add_1:0", dtype=float32)

我们可以知道：

1. x1是一个Tensor对象，Placeholder:0中的冒号后面数字代码该操作输出结果的编号，‘0’表示第一个输出结果编号，大多数情况下只有一个输出结果。type=float32表示x1是一个float32（32位浮点数）数据类型。
2. w1是一个tf.Variable对象(可变参数对象)，它不是Tensorf对象
3. n1是一个Tensor对象，是由"mul:0"操作而来的，mul是乘法（multiple）操作的简称，这个操作对应于n1=x1*w1表达式。
4. y是一个Tensor对象，是由"add_1:0"操作而来的，对应于y = n1 + n2 + n3表达式。

我们通过上述可以知道，张量在程序中有两层含义：

• 一、包含了对于输入数据的计算操作（给张量赋值时等号右边的表达式操作）
• 二、容纳一个或者一组数据，也就是它的输出数据（在程序就是张量赋值语句左边的变量）

用向量重新组织输入数据

如果现在要在三好学生中添加一个艺术分数，那么在神经网络的输入成添加一个x4节点，隐藏层添加一个n4节点。即输入数据改变时，整套逻辑没有改变，也要修改整个网络模型，这样太过于复杂。在神经网络中更多的是一串的数据组成的。如三好学生的三个分数可以用数组【90,80,70】来表示。我们把每一列称为一维，三好学生的三个分数称为一个三维向量。

简化后的代码实现：

#Author:北京
#QQ:838262020
#time:2021/3/30

# 导入TensorFlow包
import tensorflow as tf

# 定义占位符，数据类型为浮点型
x=tf.placeholder(shape=[3],dtype=tf.float32)

yTrain =tf.placeholder(shape=[],dtype=tf.float32)

# 定可变参数，数据类型为浮点型
w = tf.Variable(tf.zeros([3]),dtype=tf.float32)


n= w*x

y = tf.reduce_sum(n)

loss=abs(y-yTrain)

optimizer=tf.train.RMSPropOptimizer(0.001)

train=optimizer.minimize(loss)

# 会话对象
sess = tf.Session()

# 初始化可变参数
init = tf.global_variables_initializer()
sess.run(init)

# 输出要查看的变量和喂数据
for i in range(5000):
    result1 = sess.run([train,x,y,yTrain,loss],feed_dict={x:[90,80,70],yTrain:85})
    print(result1)
    result2 = sess.run([train,x,y,yTrain,loss],feed_dict={x:[98,95,87],yTrain:96})
    print(result2)

通过上面的代码我们可以看见：

原来的输入节点变量x1,x2,x3

x1 = tf.placeholder(dtype=tf.float32)
x2 = tf.placeholder(dtype=tf.float32)
x3 = tf.placeholder(dtype=tf.float32)

改成了一个3维的向量存入变量x:

x=tf.placeholder(shape=[3],dtype=tf.float32)

原来的可变参数w1,w2,w3：

# 定义三个可变参数，数据类型为浮点型
w1 = tf.Variable(0.1,dtype=tf.float32)
w2 = tf.Variable(0.1, dtype=tf.float32)
w3 = tf.Variable(0.1, dtype=tf.float32)

改成了一个3维向量w，tf.zeors([3])表示的是一个3维向量元都为零，即[0,0,0]。

w = tf.Variable(tf.zeros([3]),dtype=tf.float32)

原本的yTrain =tf.placeholder(dtype=tf.float32)是一个普通数字，因此我们只需要添加shape=[]，即yTrain =tf.placeholder(shape=[],dtype=tf.float32)

隐藏层节点n1,n2,n3也简化成n；

n= w*x

现在的y = tf.reduce_sum(n)代替了y=n1+n2+n3,即tf.reduce_sum函数的作用是把作为它的参数的向量（矩阵）中的所有维度的值相加求和.

概念补充--标量、多维数组、张量等

1. 标量：普通的一个数字，可以是整数或者浮点数（小数）
2. 多维数组：对应数学中的矩阵，如两个学生的分数分别为90,80,70和98,95,87，用矩阵表示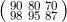，称做“2x3的矩阵”。
3. 张量的阶和形态：张量主要用来存放节点的输出数据的，其中存放的数据可以是一个标量，也可以是一个向量（一组数），还可以是一个矩阵（二维的数组），甚至可以是用多维数组来表达的数据。TensorFlow中用“形态”（shape）来表达在张量中存储的数据的形态。

注意：

       不要把向量的维度和数组的维度混淆。向量中，我们把向量中有几个数字，我们把它叫作几个维度，其中每一个数字叫作一维。在多维数组中，除了最后一维是一个一维数组外，其他每一维都是包含数组作为内容项的，并且维度越高，包含的内容项的维度也越高，比如，二维数组的第一维包含的内容项都是一维数组，而三维数组包含的内容项都是一个个二维数组。如[[[90,80,70],[98,95,87]],[[88,90,63],[93,94,34]]]，这个三维数组可以用来表示两个班级学生的成绩，也就是说在‘学生’和‘分数类型（德育、智育，体育）’的基础上，引入了“班级”的维度作为第一个维度。第一个维度包含两个班级，第二个维度是每个班级包含两个学生，第三个维度包含3个数组；这个三维数组可以称为“2x2x3的三维数组”。

在TensorFlow中查看和设定张量的形态

# Author:北京
# QQ:838262020
# time:2021/3/31
import tensorflow as tf

x = tf.placeholder(dtype=tf.float32)
xShape = tf.shape(x)
sess = tf.Session()
# 标量的形态
result = sess.run(xShape, feed_dict={x: 8})
print(result)
# 向量的形态
result = sess.run(xShape, feed_dict={x: [3, 4, 5]})
print(result)
# 向量的形态
result = sess.run(xShape, feed_dict={x: [[3, 4, 5], [2, 3, 4]]})
print(result)

运行结果

[ ]
[3]
[2 3]

softmax函数规范可变参数

       根据三好学生的计算公式：总分=德育分*0.6+智育分*0.3+体育分*0.1，我们可以看出三个权重之和为1.根据权重之和为1这个规则，我们可以使用这个规则大大减小优化器调整可变参数的工作量。

# Author:北京
# QQ:838262020
# time:2021/3/30

# 导入TensorFlow包
import tensorflow as tf

# 定义占位符，数据类型为浮点型
x = tf.placeholder(shape=[3], dtype=tf.float32)

yTrain = tf.placeholder(dtype=tf.float32)

# 定可变参数，数据类型为浮点型
w = tf.Variable(tf.zeros([3]), dtype=tf.float32)

wn = tf.nn.softmax(w)

n = x * wn

y = tf.reduce_sum(n)

loss = abs(y - yTrain)

optimizer = tf.train.RMSPropOptimizer(0.1)

train = optimizer.minimize(loss)

# 会话对象
sess = tf.Session()

# 初始化可变参数
init = tf.global_variables_initializer()
sess.run(init)

# 输出要查看的变量和喂数据
for i in range(5):
    result1 = sess.run([train, x, w, wn, y, yTrain, loss], feed_dict={x: [90, 80, 70], yTrain: 85})
    print(result1[3])
    result2 = sess.run([train, x, w, wn, y, yTrain, loss], feed_dict={x: [98, 95, 87], yTrain: 96})
    print(result2[3])

运行结果：

[ 0.33333334  0.33333334  0.33333334]
[ 0.41399801  0.32727832  0.25872371]
[ 0.44992     0.32819405  0.22188595]
[ 0.52847189  0.2905868   0.18094125]
[ 0.5593363   0.28043905  0.1602246 ]
[ 0.63181394  0.23469751  0.13348855]
[ 0.6576013   0.22204098  0.12035771]
[ 0.59303778  0.26626641  0.14069577]
[ 0.6190725   0.25382361  0.12710389]
[ 0.68249691  0.20963639  0.1078667 ]

我们可以看见wn三个数之和一直为1。三好学生模型是典型的线性问题，线性问题是神经网络中最简单的一类。我们的问题符合y=wx或者（y=wx+b）。