七大排序算法总结

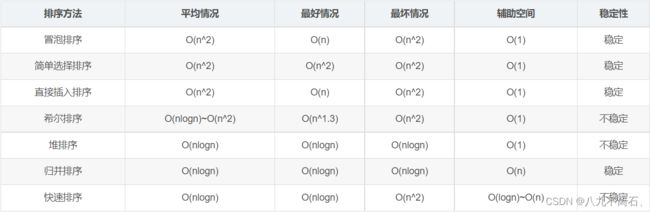
1.稳定性(重要)

俩个相等的数据,如果经过排序后,排序算法能保证其相对位置不发生变化,则我们称该算法是具备稳定性的排序算法.

例如:某宝商城后台,需要你按照订单的金额排序,原订单是按照时间顺序排的,要求排序后原先的时间先后顺序不变,即为稳定性.

这时候就需要我们使用稳定性的排序算法对订单的金额进行升序排序,保证其他信息的先后顺序不发生变化.

2.分类:

内排序:一次性将所有待排序的数据放入内存中进行的排序,基于元素之间比较的排序.包括七大排序

外排序：需要在内外存之间多次交换数据才能进行.包括桶排序,基数排序,计数排序,对于数据集合的要求非常高,只能在特定的场合下使用

注意:写排序的代码,一定要注意变量是如何定义的,以及未排序区间和已排序区间的定义.

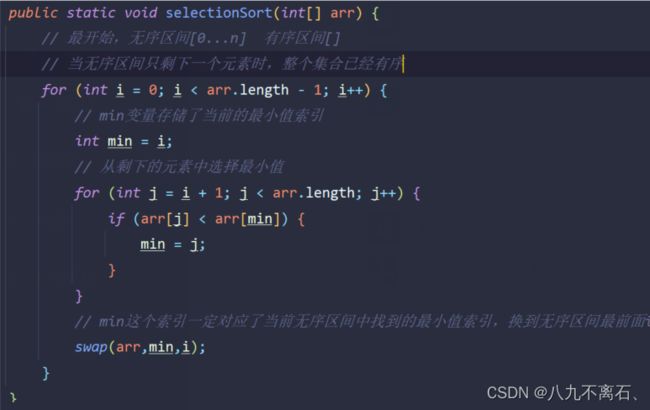
1.选择排序:

每次从无序区间中选择一个最大或最小值,存放在无序区间的最前或最后的位置(此位置的元素以及有序),直到所有的数据都排序完成为止.

代码示例如下:

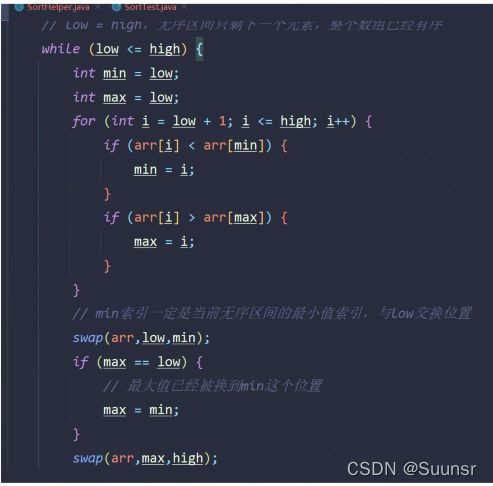
关于选择排序,我们可以进一步优化为双向选择排序:

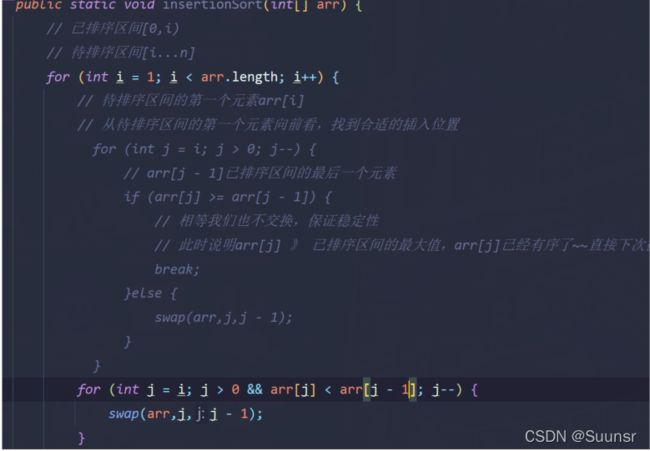
 2.插入排序:

将集合分为俩个区间:一个为已经排序的区间,一个为待排序的区间,然后每次从待排序区间中选择一个元素插入到已经排序好的区间,直到整个数组有序

插入排序和选择排序最大的不同在于:当插入排序当前遍历的元素>前驱元素时,此时可以提前结束内层循环,极端场景下,当集合是一个完全有序的集合,插入排序的内层循环一次都不走,时间复杂度就变为了O(n),所以插入排序经常用作高阶排序算法的优化手段之一.

3.希尔排序:缩小增量排序

先选定一个整数(gap,gap一般都选取数组长度的一半或者1/3),将待排序的数组先按照gap分组,不同组之间使用插入排序,排序之后,再将gap/2或者/3.重复上述流程,直到gap=1,当gap=1时,整个数组已经被调整的近乎有序,此时就是使用插入排序最好的时机,最后在整个数组上使用一次插入排序即可.

4.归并排序:

将原数组不断拆分,一直拆到每个子数组只有一个元素时,第一阶段结束,归而为1这个阶段结束

并:将相邻的俩个数组合并为一个有序的数组,直到整个数组有序,归并排序是一个稳定的nlogn排序算法

归并排序的优化:

a.当左右俩个子区间走完子函数之后,左右俩个区间已经有序了,如果此时arr[mid]

arr[mid]已经是左区间的最大值,arr[mid] + 1已经是右区间的最小值了,这代表整个区间已经有序,没必要在执行merge过程.

b.在小区间上,我们可以直接使用插入排序来优化,没必要元素一直拆分到1位置,r-l<=15,使用插入排序性能是很好的,可以减少归并的递归次数

归并的应用:海量数据的排序处理

假设现在待排序的数据有100G,但是内存只有1GB,如何排序这100GB的数据呐?

1.先将这100GB的数据分别存储在200个文件中(存储在硬盘),每个文件都是0.5G

2.分别将这200个文件依次读取到内存中,使用任何一个内部排序算法对其排序,此时就可以得到200个已经有序的文件

3.分别对这200个文件merge操作即可.

那么如何具体操作?

这200个小文件已经有序,每次都取出200个文件的第一个元素放到内存中,内部排序这200个小值的最小值写回大文件的第一行,重复上述流程,直到这200个文件所有内容全部写会大文件即可

5.快速排序:

先介绍快排的分区思想:

 对于快排的基准值选择,我们一开始默认是选择第一个元素作为分区点,如果在极端情况下,数组就是一个完全有序的数组,此时分区的左右俩个严重不平衡,二叉树退化为单支树,树结构就退化为了链表,递归的过程实际就是在遍历数组,O(N^2)的算法,所以我们在选择基准值的时候,采用随机选择的方法或者是几数去中,一般都是三数取中,在有大量重复元素的集合上,快排依然会退化,这时我们采用二路快排或者三路快排.