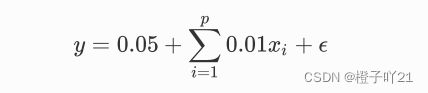动手学深度学习——权重衰退及代码实现

一、权重衰退

1、权重衰退：是常用来处理过拟合的一种方法。

2、使用均方范数作为硬性限制

通过限制参数值的选择范围来控制模型容量

• 通常不限制偏移b（限制不限制都差不多）。
• 小的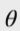意味着更强的正则项。

3、使用均方范数作为柔性限制

对于每个，都可以找到λ使得之前的目标函数等价于下面：

可以通过拉格朗日乘子来证明。

超参数λ控制了正则项的重要程度：

4、参数更新法则

每一次引入λ就会把权重放小，所以叫权重衰退。

5、总结

权重衰退通过L2正则项使得模型参数不会过大，从而控制模型复杂度。

正则项权重是控制模型复杂度的超参数。

二、代码实现

下⾯，我们以⾼维线性回归为例来引⼊⼀个过拟合问题，并使⽤权᯿衰减来应对过拟合。设数据样本特 征的维度为p 。对于训练数据集和测试数据集中特征为x1，x2,....xp的任⼀样本，我们使⽤如下的线性 函数来⽣成该样本的标签：

 

 偏差0.05+权重0.01乘以随机的输入x然后+噪音，均值为0，方差为0.01的正态分布.

import torch
import torch.nn as nn
import numpy as np
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
import sys
from matplotlib import pyplot as plt
"""
生成一个人工数据集，还是一个线性回归的问题，
偏差0.05+权重0.01乘以随机的输入x然后+噪音，均值为0，方差为0.01的正态分布
"""
n_train, n_test, num_inputs = 20, 100, 200
#训练数据集越小，越容易过拟合。训练数据集为20，测试数据集为100，特征的纬度选择200.
#数据越小，模型越简单，过拟合越容易发生

true_w, true_b = torch.ones(num_inputs, 1) * 0.01, 0.05
#真实的权重就是0.01*全1的一个向量，偏差b为0.05

"""
读取一个人工的数据集
"""
features = torch.randn((n_train + n_test, num_inputs)) #特征
labels = torch.matmul(features, true_w) + true_b #样本数
labels += torch.tensor(np.random.normal(0, 0.01,size=labels.size()), dtype=torch.float)
train_features, test_features = features[:n_train, :],features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]

"""
初始化模型，该函数为每个参数都附上梯度
"""
def init_params():
    w=torch.randn((num_inputs,1),requires_grad=True)
    b=torch.zeros(1,requires_grad=True)
    return [w,b]

"""
定义L2范数惩罚，只惩罚模型的权重参数
"""
def l2_penalty(w):
    return (w**2).sum()/2

"""
定义训练和测试模型
"""
batch_size, num_epochs, lr = 1, 100, 0.003
net, loss = d2l.linreg, d2l.squared_loss
dataset = torch.utils.data.TensorDataset(train_features,train_labels)
train_iter = torch.utils.data.DataLoader(dataset, batch_size,shuffle=True)

def fit_and_plot(lambd):
    w,b=init_params()
    train_ls,test_ls=[],[]
    for _ in range(num_epochs):
        for X,y in train_iter:
    # 添加了L2范数惩罚项
            l=loss(net(X,w,b),y)+lambd*l2_penalty(w)
            l=l.sum()
            if w.grad is not None:
                w.grad.data.zero_()
                b.grad.data.zero_()
            l.backward()
            d2l.sgd([w, b], lr, batch_size)
        train_ls.append(loss(net(train_features, w, b),train_labels).mean().item())
        test_ls.append(loss(net(test_features, w, b),test_labels).mean().item())
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs','loss',
                     range(1, num_epochs + 1), test_ls, ['train','test'])
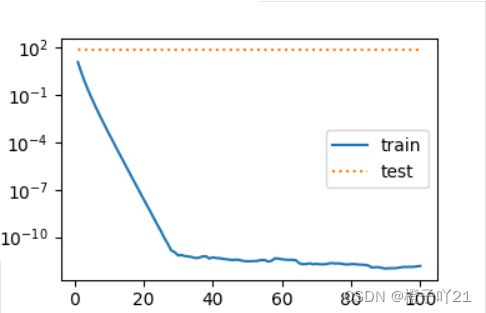
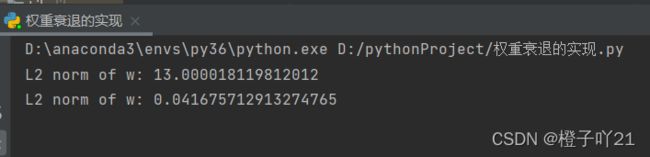
    print('L2 norm of w:', w.norm().item())

当 lambd 设为0时，我们没有使⽤权重衰减。
结果训练误差远⼩于测试集上的误差。这是典型的过拟合现象.

fit_and_plot(lambd=0)
plt.show()

 

 

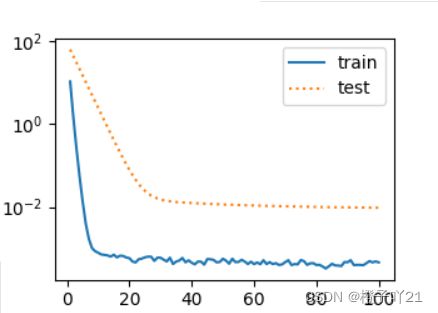
这里使⽤权重衰减。可以看出，训练误差虽然有所提⾼，但测试集上的误差有所下降。过拟合现象得到⼀定程度的缓解。
另外，权重参数的L2 范数⽐不使⽤权᯿衰减时的更⼩，此时的权重参数更接近0

fit_and_plot(lambd=3)
plt.show()