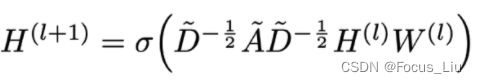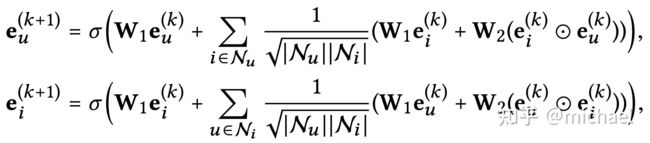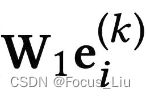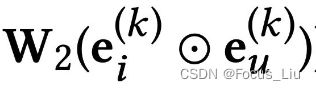图神经网络-GCN、GraphSAGE、NGCF、LightGCN

本篇主要讲解GCN、GraphSAGE、NGCF、LightGCN。

基础概念

---

图的分类：

同构图：图中只有一种类型的节点、一种类型的边。

异构图：图中有多种类型的节点 或 多种类型的边。

什么是二部图？

Graph由两类节点组成（例：User、Item），且节点的链接关系都是U-I-U-I...不存在I-I、U-U相连的情况。

第三方库-图神经网络DGL

进行图神经网络的搭建，我们可以使用tf和pytory原生的api，但是效率一版。DGL库提升的api对于图场景进行优化，支持tf和pytory，能更快的构建、传递、聚合。

Graph Embedding两大类：

浅层图模型：DeepWalk、Node2Vec、LINE

深度图模型：

①基于谱的卷积——频域（谱域）（spectral domain） 

算法：GCN算法

解释：频域可以类比到对图片进行傅里叶变换后，再进行卷积。（通过对图的拉普拉斯矩阵做特征分解，将它定义在傅里叶 domain上）。

②基于空间的卷积——顶点域（空间域） （vertex domain）

算法：GraphSAGE

解释：图片的卷积知道吧，图的空间卷积就是节点当做图的像素点进行卷积

常见图算法：

NGCF：是一个用于协同过滤的笨重GCN模型

GCN+Attention 的思路很棒，有 GAT 和 AGNN。

GCN+Pooling 的思路很棒，有 GraphSAGE。

GCN+Deep 的思路很棒，有 DeepGCN。​

将GCN应用于推荐系统的协同过滤模型中，NGCF。

---

第一章-GCN（图卷积）

GCN代码讲解

adj, features, y_train, y_val, y_test, train_mask, val_mask, test_mask = load_data(FLAGS.dataset)

• adj：邻接矩阵，0-1矩阵。shape是2708*2708（节点数*节点数），相连就是1不相连是0。由于比较稀疏，邻接矩阵格式是LIL的。
• features：一个tuple，构建特征矩阵所需的三个对象。coords, values, shape。coords是矩阵中有值的坐标，values是坐标具体的值，shape就是矩阵的维度，shape(2708, 1433)，节点数*特征数。特征矩阵是用来查询每个节点的特征。
• y_train, y_val, y_test：shape都是(2708, 7)，节点数*类别数。一共7类，所属类别为1。每行只有一个为1。即y_train的值为对应与labels中train_mask为True的行，其余全是0。
• train_mask, val_mask, test_mask：shaped都为(2708, )的向量，但是train_mask中的[0,140)范围的是True，其余是False；val_mask中范围为(140, 640]范围为True，其余的是False；test_mask中范围为[1708,2707]范围是True，其余的是False

features = preprocess_features(features)  

该操作是特征矩阵（行）归一化。这里是用的是让每个维度除以向量的L1范数。处理前features是(2708, 1433)的稀疏矩阵，只有部分值为1，按照行进行归一化后，现在把每行变成一个单位向量。例如第一行只有[19, 81, 146, 315, 774, 877, 1194, 1247, 1274]为1，归一化后，[19, 81, 146, 315, 774, 877, 1194, 1247, 1274]的值都为0.11111

代码变量

adj：邻接矩阵A（一个用来描述节点是否相连的0-1矩阵，Ai和Aj相连那，Aij就是1，Aji也是1）。
support：是邻接矩阵的对称归一化形式。即support=D~(-1/2)·A~·D~(-1/2)，其中A~是A+I。

support

support = [preprocess_adj(adj)]

support：是邻接矩阵（adj）的归一化形式，

placeholders = {
    'support': [tf.sparse_placeholder(tf.float32) for _ in range(num_supports)],
    'features': tf.sparse_placeholder(tf.float32, shape=tf.constant(features[2], dtype=tf.int64)),
    'labels': tf.placeholder(tf.float32, shape=(None, y_train.shape[1])),
    'labels_mask': tf.placeholder(tf.int32),
    'dropout': tf.placeholder_with_default(0., shape=()),
    'num_features_nonzero': tf.placeholder(tf.int32)  # helper variable for sparse dropout
}

对于feed_dict输入的说明：

• labels：(2708, 7)，即每个节点都属于那个分类。
• labels_mask：[ True,  True,  True, ..., False, False, False]，
• features：构建特征稀疏矩阵的三元素。(2708, 1433)
• support：是邻接矩阵（adj）的归一化形式。也是三元素。
• num_features_nonzero：features矩阵中，元素不为0的个数。矩阵dropout的时候用。
• dropout：丢弃率，0.5。

注意每步训练feed_dict都是不变的，每次都放入了全量的数据。

---

①GCN核心公式？

H(l)：GNN层的输入（一般为节点数*节点向量维度）
H(l+1)：GNN层的输出
A：节点的邻接矩阵
A~：A+I，自循环。（实际上，就是把邻接矩阵A对角线上的数，全部由0变为1）
D~：A~对应的度矩阵。
W(l)：第l层的权重
b(l)：第l层的截距

解释：
GCN公式：H(l+1)=σ(D~(-1/2)·A~·D~(-1/2)·H(l)·W(l))看着挺复杂，但其实D~(-1/2)·A~·D~(-1/2)是为了对A~进行对称归一化。所以其整体形式可以看做：H(l+1)=σ(处理后的A·H(l)·W(l))

②什么是邻接矩阵A？什么是度矩阵D？

                      

例如对于上图，当给了一张图，我们有了它的邻接矩阵A和度矩阵D。

邻接矩阵A：是一个0-1矩阵，记录着任意两个节点是否相连，记录着图的全部信息。
度矩阵D：是一个对角矩阵，记录着每个节点的邻居个数，可由A算出D。

③如何计算拉普拉斯矩阵？

其实很简单，就是D−A。

④A~是啥，D~是啥？

A~读做“A hat”，它由A+I而来（自循环），实际上，就是把邻接矩阵A对角线上的数由0变为1。
D~就是A~对应的度矩阵。

⑤什么叫对一个矩阵进行“对称归一化”？

例如我们有一个矩阵A，我们对它进行对称归一化就是D(-1/2)·A·D(-1/2)，其中D是A的度矩阵。在GCN的实现时，有人是对邻接矩阵A进行对称归一化，有人是对由A和D算得的拉普拉斯矩阵L进行对称归一化。

⑥GNN和GCN的关系？

一般来讲，一个GCN由两个GNN层组成。

背景：有2078篇论文，每篇论文有1433个特征和一个所属分类（共7类）。训练一个分类模型，输入一篇新论文然后得出这篇论文属于七类中的哪一类。
模型流转：第一层GNN：输入1433维度（特征个数），卷积变成16维度（可变）。第二层GNN：输入16维度，输出7维度（类别总数）。

⑦GCN最大的三个缺点：

1.冷启动问题：因为是直推式transducive，无法直接泛化到新加入（未见过）的节点。

2.无法应用到大图：实践受限。（因为每次卷积都是全部的邻接矩阵）

3.不能处理有向图：（因为在特征分解时需要拉普拉斯矩阵L，是对称矩阵）

⑦masked_softmax_cross_entropy：mask在半监督的用法
半监督意义：样本不需要都有label，也可以训练出一个分类模型。
mask使用思路：共有2708个节点，建一个长2708的mask数组，值为0或1。训练算loss的时候，只算mask值为1的样本的loss（样本按照mask值为1所占比例提权）。比如100个数据中训练集已知带标签的数据有50个， 那么计算损失的时候，loss 乘以的 mask 是以前的2倍，

⑧GCN为什么先做傅里叶变换，再卷积呢：

Graph和Image数据的差别在于节点的邻居点个数、顺序都是不定的，使得传统用于Image上的卷积操作不能直接用在图上，因此需要从谱域(Spectral Domain)上重新定义卷积操作再通过卷积定理转换回空间域上。

GCN流程：

1⃣️先对features系数矩阵，进行dropout，得到新的features，(2708, 1433)。

2⃣️申请一个（input_dim,output_dim）的权重。得到weights_0，(1433, 16)。

3⃣️然后，features和weights_0 ，进行稀疏矩阵和稠密矩阵的相乘，得到稠密矩阵pre_sup。(2708, 16)

4⃣️然后，使用邻接矩阵的归一化形式support（2708, 2708）和上次一结果pre_sup，进行稀疏矩阵和稠密矩阵的相乘，得到output，（2708,16）

5⃣️重复把输出维度改成label个数，重复3～4

结合GCN的公式解释GNNLayer源码：

    def _call(self, inputs):
        x = inputs #2708 1433
        # 加dropout
        if self.sparse_inputs:
            x = sparse_dropout(x, 1-self.dropout, self.num_features_nonzero)
        else:
            x = tf.nn.dropout(x, 1-self.dropout)
        # convolve
        supports = list()
        """
            GCN论文公式：
                H(l+1)=σ(D~(-1/2)·A~·D~(-1/2)·H(l)·W(l))
            代码实现公式：
                H(l+1)=σ(归一化后的A·H(l)·W(l))
            原理说明：
                ①其实论文中进行D~(-1/2)·A~·D~(-1/2)，为了对A~进行归一化（行之和为1）。
                ②A~ 由A+I而来，即引入了自循环。（实际上，就是把邻接矩阵A对角线上的数，全部由0变为1）
                ③个人理解GCN都是 都是邻接矩阵的一种变换形式，与H(l)、W(l)相乘，得到输出。
            代码实现：
                x：第i层的输入。即公式中的 H(l)
                vars['weights_0']：权重。即公式中的W(l)
                support[0]：归一化后的邻接矩阵A
        """
        for i in range(len(self.support)):
            pre_sup = dot(x, self.vars['weights_' + str(i)],sparse=self.sparse_inputs) #
            support = dot(self.support[i], pre_sup, sparse=True)
            supports.append(support)
        output = tf.add_n(supports)
        if self.bias:
            output += self.vars['bias']
        return self.act(output)

半监督Mask的用法解释：

def masked_softmax_cross_entropy(preds, labels, mask):
    """Softmax cross-entropy loss with masking."""
    loss = tf.nn.softmax_cross_entropy_with_logits(logits=preds, labels=labels)#计算交叉熵
    mask = tf.cast(mask, dtype=tf.float32)#tf.cast()转换数据类型   train_mask [1,1,1,1..0,0,0,0] 140个1，2567个0
    mask /= tf.reduce_mean(mask) #计算各维度上的均值  把mask转成权重，1->19.3  0->0
    loss *= mask #  只算mask等于1的样本的loss
    return tf.reduce_mean(loss)

• GCN整个网络里面就只有两个variables，也就是两个weights： weights1:维度（1433,16） weights2:维度（16,7）
  1433：是输入维度，代码中是指的1433个特征（也可以是给每个特征embedding后再concat作为输入维度）。
  16：中间维度，中间映射到多少都行。
  7：最终维度，也就是label的个数。

• 一句概括GNN：
  第一步：features（节点数*特征数）*weights（特征数*输出维度）得到pre_sup（节点数*输出维度），
  第二步：support（节点数*节点数）*pre_sup得到output（节点数*输出维度）。

• 两层GNN和两个MLP的区别是：MLP没有第二步（没有用到support邻接矩阵）。

• 提供了可供选择的三个模型：‘gcn’, ‘gcn_cheby’, ‘dense’。MLP是由两层的dense层构成

• Cora数据集说明：2708个节点，1435列（1433个特征，1列id，1列类别-label），7分类。
  日志Dataset has 2708 nodes, 5429 edges, 1433 features.

参考资料：

GCN(Graph Convolutional Network)的简单公式推导 - denny402 - 博客园

https://zhuanlan.zhihu.com/p/358758581

详解GCN原理-公式推导_SperNijia的博客-CSDN博客_gcn公式

图卷积网络GCN代码分析（Tensorflow版）_不务正业的土豆的博客-CSDN博客_gcn tensorflow

工作台 - Heywhale.com

【总结】推荐系统——召回篇【3】 - 知乎

---

第二章-GraphSAGE篇

GraphSAGE的计算流程主要包含三个部分：

• 邻居节点采样：对图中每个节点的邻居节点进行采样。
   
• 聚合函数生成节点Embedding：根据聚合函数聚合邻居节点特征，生成当前节点Embedding。
• 预测输出：使用聚合函数生成的节点Embedding，预测输出概率。

GraphSAGE聚合函数：

---

 第三章-NGCF篇（神经图协同过滤）

背景：传统的协同过滤（基于矩阵分解or深度学习）忽略了user-item在交互过程中产生的协作信号。（u1点了u2点过的商品i2。其实是把u2的某些特性通过i2传递给了u1）

公式：

公式说明：

整体可以看做： User向量=激活函数（邻居User聚合 + （邻居item聚合 + 通过Item传过来User的信息聚合））

：代表对所有当前u的所有邻居User向量的加权求和。

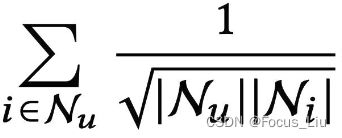：对所有User相邻的Item做加权求和，Nu代表User相邻Item的个数，Ni代表当前Item相邻User的个数。

：代表对所有当前u的所有邻居Item向量的加权求和。

：圈点代表元素积，即按位置相乘。

---

 第四章-LightGCN篇（轻量图卷积）

①lightGCN是对NGCF的化简，按如以下三种方案去掉参数，发现效果没有下降。

ngcf-f：在NGCF基础上，剔除特征变换矩阵（w1和w2）

ngcf-n：在NGCF基础上，剔除非线性激活函数σ。

ngcf-fn：在NGCF基础上，同时剔除特征变化和非线性激活函数。

②lightGCN和NGCF的关系：

lightGCN简化了NGCF，在NGCF的基础上删去了变换矩阵和激活函数。改成了把单独的GCN层加权求和。

③lightGCN公式：

 说明：

第一步：Normalized Sum进行层卷积，得到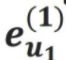~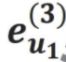（相当于每个user在每个层表示）。 

第二步：Weighted Sum合并 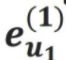~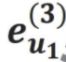还有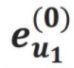，得到同时考虑本身和最近3跳的user向量表示。

第三步：重复一二得到Item的向量表示。User向量点乘Item向量得到score去拟合label。

d

light-gcn代码讲解：

git地址：GitHub - kuandeng/LightGCNContribute to kuandeng/LightGCN development by creating an account on GitHub.https://github.com/kuandeng/LightGCN

所需数据：

train.txt：uid->itemid集合
test.txt：uid->itemid集合
user_list：原始uid到编码uid的映射
item_list：原始itemid到编码itemid的映射

参考资料：图神经网络：NGCF, LightGCN小结 - 知乎

---