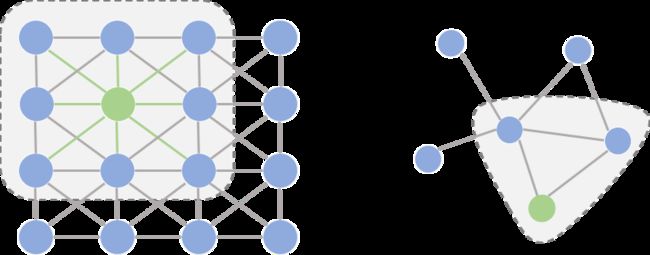
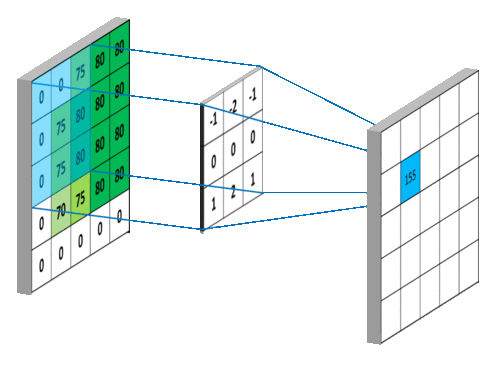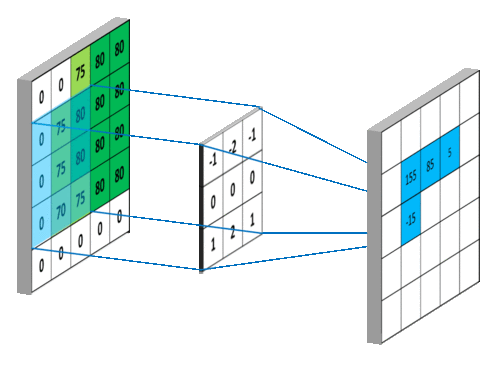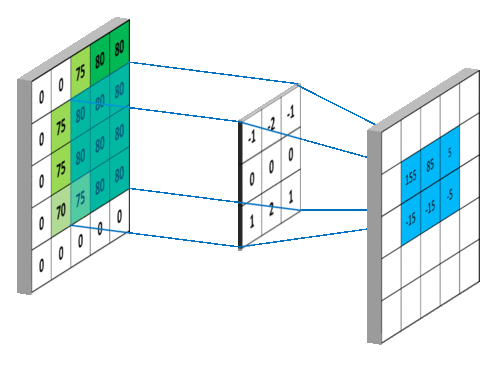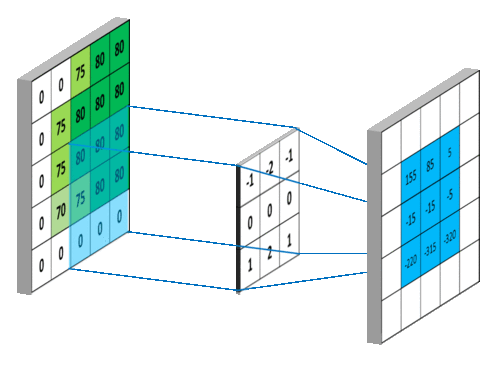
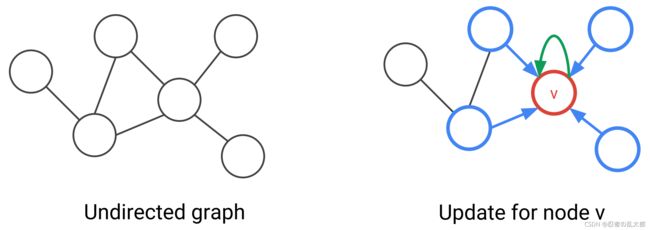
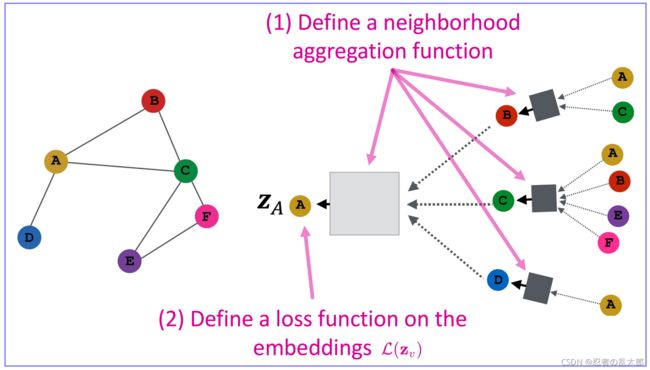
GNN:“图卷积模型”通用框架【每一层网络都基于邻域节点(1-hop)更新当前节点的向量表示(一般用2~3层)】【消息传递:①从邻域节点汇聚信息;②更新当前节点状态】【各模型区别:聚合函数类型的选取】
一、卷积的概念
1、图卷积缘起
在开始正式介绍图卷积之前,我们先花一点篇幅探讨一个问题:为什么研究者们要设计图卷积操作,传统的卷积不能直接用在图上吗? 要理解这个问题,我们首先要理解能够应用传统卷积的**图像(欧式空间)与图(非欧空间)**的区别。
如果把图像中的每个像素点视作一个结点,如下图左侧所示,一张图片就可以看作一个非常稠密的图;下图右侧则是一个普通的图。
阴影部分代表卷积核,左侧是一个传统的卷积核,右侧则是一个图卷积核。卷积代表的含义我们会在后文详细叙述,这里读者可以将其理解为在局部范围内的特征抽取方法。
仔细观察两个图的结构,我们可以发现它们之间有2点非常不一样:
- 在图像为代表的欧式空间中,结点的邻居数量都是固定的。比如说绿色结点的邻居始终是8个(边缘上的点可以做Padding填充)。但在图这种非欧空间中,结点有多少邻居并不固定。目前绿色结点的邻居结点有2个,但其他结点也会有5个邻居的情况。
- 欧式空间中的卷积操作实际上是用固定大小可学习的卷积核来抽取像素的特征,比如这里就是抽取绿色结点对应像素及其相邻像素点的特征。但是因为图里的邻居结点不固定,所以传统的卷积核不能直接用于抽取图上结点的特征。
真正的难点聚焦于邻居结点数量不固定上。那么,研究者如何解决这个问题呢?其实说来也很简单,目前主流的研究从2条路来解决这件事:
- 提出一种方式把非欧空间的图转换成欧式空间。
- 找出一种可处理变长邻居结点的卷积核在图上抽取特征。
这两条实际上也是后续图卷积神经网络的设计原则,图卷积的本质是想找到适用于图的可学习卷积核。
2、图卷积框架(Framework)
上面说了图卷积的核心特征,下面我们先来一窥图卷积神经网络的全貌。如下图所示,输入的是整张图:
- 在
Convolution Layer 1里,对每个结点的邻居都进行一次卷积操作,并用卷积的结果更新该结点;然后经过激活函数如ReLU, - 然后再过一层卷积层
Convolution Layer 2与一次激活函数; - 反复上述过程,直到层数达到预期深度。
与GNN类似,图卷积神经网络也有一个局部输出函数,用于将结点的状态(包括隐藏状态与结点特征)转换成任务相关的标签,比如水军账号分类,本文中笔者称这种任务为Node-Level的任务;也有一些任务是对整张图进行分类的,比如化合物分类,本文中笔者称这种任务为Graph-Level的任务。卷积操作关心每个结点的隐藏状态如何更新,而对于Graph-Level的任务,它们会在卷积层后加入更多操作,从结点信息得到整张图的表示。
GCN与GNN乍看好像还挺像的,它们根本上的不同:GCN是多层堆叠,比如上图中的Layer 1和Layer 2的参数是不同的;GNN是迭代求解,可以看作每一层Layer参数是共享的。
3、卷积(Convolution)
图卷积神经网络主要有两类,一类是基于空域的,另一类则是基于频域的。
通俗点解释,空域可以类比到直接在图片的像素点上进行卷积,而频域可以类比到对图片进行傅里叶变换后,再进行卷积。
傅里叶变换的概念我们先按下不讲,我们先对两类方法的代表模型做个大概介绍。
基于空域卷积的方法直接将卷积操作定义在每个结点的连接关系上,它跟传统的卷积神经网络中的卷积更相似一些。在这个类别中比较有代表性的方法有:
- Message Passing Neural Networks(MPNN)《Neural Message Passing for Quantum Chemistry》,
- GraphSage《Inductive Representation Learning on Large Graphs》,
- Diffusion Convolution Neural Networks(DCNN)《Diffusion-Convolutional Neural Networks》,
- PATCHY-SAN《Learning Convolutional Neural Networks for Graphs》。
基于频域卷积的方法则从图信号处理起家,包括:
- Spectral CNN《Spectral Networks and Locally Connected Networks on Graphs》,
- Cheybyshev Spectral CNN(ChebNet)《Convolutional neural networks on graphs with fast localized spectral filtering》,
- First order of ChebNet(1stChebNet)《Semi-Supervised Classification with Graph Convolutional Networks》。
在介绍这些具体的模型前,先让我们从不同的角度来回顾一下卷积的概念,重新思考一下卷积的本质。
3.1 基础概念
由维基百科的介绍我们可以得知,卷积是一种定义在两个函数( f f f跟 g g g)上的数学操作,旨在产生一个新的函数。那么 f f f 和 g g g 的卷积就可以写成 f ∗ g f*g f∗g ,数学定义如下:
( f ∗ g ) ( t ) = ∫ − ∞ ∞ f ( τ ) g ( t − τ ) ( 连 续 形 式 ) (f*g)(t)={\int}_{-\infty}^{\infty}f(\tau)g(t-\tau) (连续形式) (f∗g)(t)=∫−∞∞f(τ)g(t−τ)(连续形式)
( f ∗ g ) ( t ) = ∑ τ = − ∞ ∞ f ( τ ) g ( t − τ ) ( 离 散 形 式 ) (f*g)(t)={\sum}_{\tau=-\infty}^{\infty}f(\tau)g(t-\tau) (离散形式) (f∗g)(t)=∑τ=−∞∞f(τ)g(t−τ)(离散形式)
离散卷积本质就是一种加权求和。
3.2 实例:掷骰子问题
光看数学定义可能会觉得非常抽象,下面我们举一个掷骰子的问题,该实例参考了知乎问题"如何通俗易懂地解释卷积"《如何通俗易懂地解释卷积》的回答。
想象我们现在有两个骰子,两个骰子分别是 f f f 跟 g g g, f ( 1 ) f(1) f(1) 表示骰子 f f f 向上一面为数字 1 1 1 的概率。同时抛掷这两个骰子1次,它们正面朝上数字和为 4 4 4 的概率是多少呢?相信读者很快就能想出它包含了三种情况,分别是:
- f f f 向上为1, g g g 向上为3;
- f f f 向上为2, g g g 向上为2;
- f f f 向上为3, g g g 向上为1;
最后这三种情况出现的概率和即问题的答案,如果写成公式,就是 ∑ τ = 1 3 f ( τ ) g ( 4 − τ ) \sum_{\tau=1}^{3}f(\tau)g(4-\tau) ∑τ=13f(τ)g(4−τ)。可以形象地绘制成下图:

如果稍微扩展一点,比如说我们认为 f ( 0 ) f(0) f(0) 或者 g ( 0 ) g(0) g(0) 等是可以取到的,只是它们的值为 0 而已。那么该公式可以写成 ∑ τ = − ∞ ∞ f ( τ ) g ( 4 − τ ) \sum_{\tau=-\infty}^{\infty}f(\tau)g(4-\tau) ∑τ=−∞∞f(τ)g(4−τ)。仔细观察,这其实就是卷积 ( f ∗ g ) ( 4 ) (f*g)(4) (f∗g)(4)。
如果将它写成内积的形式,卷积其实就是:
[ f ( − ∞ ) , ⋯ , f ( 1 ) , ⋯ , f ( ∞ ) ] ⋅ [ g ( ∞ ) , ⋯ , g ( 3 ) , ⋯ , g ( − ∞ ) ] [f(-\infty),\cdots,f(1),\cdots,f(\infty)] \cdot [g(\infty),\cdots,g(3),\cdots,g(-\infty)] [f(−∞),⋯,f(1),⋯,f(∞)]⋅[g(∞),⋯,g(3),⋯,g(−∞)]
这么一看,是不是就对卷积的名字理解更深刻了呢?
所谓卷积,其实就是把一个函数卷(翻)过来,然后与另一个函数求内积。
对应到不同方面,卷积可以有不同的解释:
- g g g 既可以看作我们在深度学习里常说的核(Kernel),也可以对应到信号处理中的滤波器(Filter);
- f f f 可以是我们所说的机器学习中的特征(Feature),也可以是信号处理中的信号(Signal)。
- f f f 和 g g g 的卷积 ( f ∗ g ) (f*g) (f∗g) 就可以看作是对 f f f 的加权求和。
下面两个动图就分别对应信号处理《https://en.wikipedia.org/wiki/Convolution》与深度学习中卷积操作的过程《https://mlnotebook.github.io/post/CNN1/》。
4、直推式学习 v.s. 归纳式学习
直推式学习:训练的节点、预测的节点都必须在同一个图上;比如GCN模型
- Training algorithm sees all node features during training;
- Trains on the labels of the training Nodes
归纳式学习:训练的节点在图A中,预测的节点在图B中;比如:GraphSAGE、GAT模型;
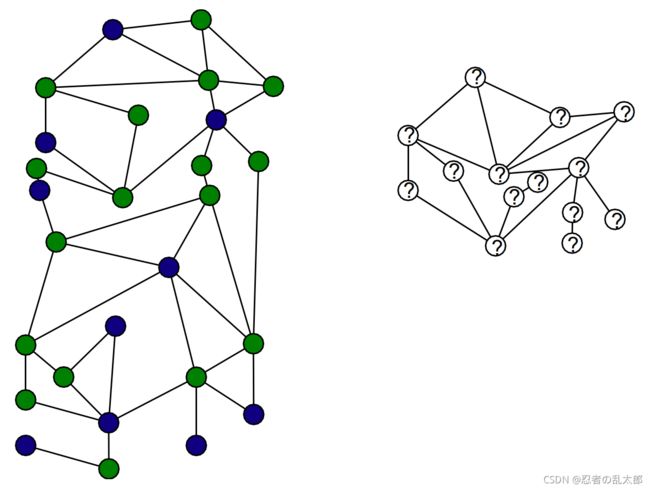
- Algorithm does not see test nodes during training;
- Significantly more challenging than transductive task;
二、“图卷积模型”通用结构
直觉:基于邻域节点生成当前节点的嵌入向量。【Intuition:Generate node embedding based on local network neighborhoods.】
图中的各个节点使用神经网络聚合来自其邻居的信息【Nodes aggregate information from their neighbors using neural networks】
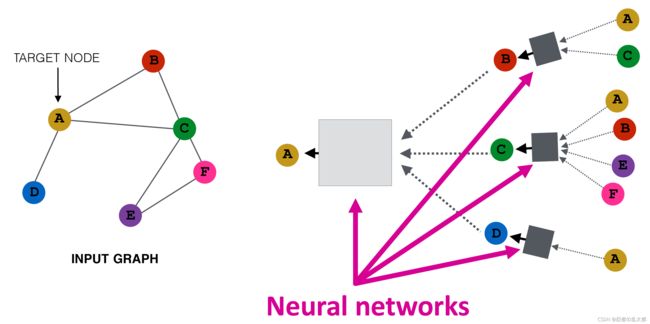
1、基本定义
给定一个图 G \color{D60595}{G} G:
- \color{D60595}{} V is the vertex set【顶点集合】;
- \color{D60595}{} v: a node in ; : the set of neighbors of .
- A \color{D60595}{A} A is the adjacency matrix (assume binary) 【邻接矩阵】,为模型的输入数据;
- X ∈ R m × ∣ V ∣ \color{D60595}{X ∈ \R^{m×|V|}} X∈Rm×∣V∣ is a matrix of node features 【节点属性】,为模型的输入数据(人工抽取、构建);
- 节点属性包括:
- Social networks: User profile, User image
- Biological networks: Gene expression profiles, gene functional information
- Node degrees, clustering coefficients, etc.
- When there is no node feature in the graph dataset:
- Indicator vectors (one-hot encoding of a node)
- Vector of constant 1: [1, 1, …, 1]
2、消息传递
3、“图卷积模型”的一层Layer中节点的信息汇聚(Building Layer of GNNs )
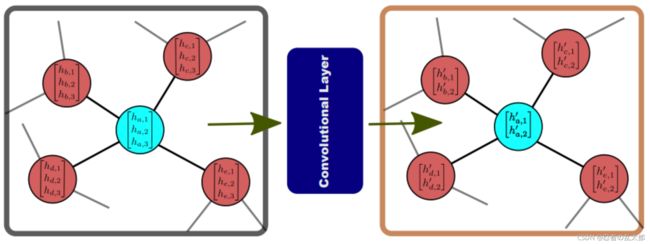
For each node in the graph, a convolutional operator consists of two main steps
- Aggregation of neighbouring node features(得到 [ h a , 1 t e m p h a , 2 t e m p h a , 3 t e m p ] \begin{bmatrix}h^{temp}_{a,1}\\h^{temp}_{a,2}\\h^{temp}_{a,3}\end{bmatrix} ⎣⎡ha,1tempha,2tempha,3temp⎦⎤):
- h a , 1 t e m p = A g g r e g a t i o n ( h a , 1 , h b , 1 , h c , 1 , h d , 1 , h e , 1 ) h^{temp}_{a,1} = Aggregation(h_{a,1},h_{b,1},h_{c,1},h_{d,1},h_{e,1}) ha,1temp=Aggregation(ha,1,hb,1,hc,1,hd,1,he,1);
- h a , 2 t e m p = A g g r e g a t i o n ( h a , 2 , h b , 2 , h c , 2 , h d , 2 , h e , 2 ) h^{temp}_{a,2} = Aggregation(h_{a,2},h_{b,2},h_{c,2},h_{d,2},h_{e,2}) ha,2temp=Aggregation(ha,2,hb,2,hc,2,hd,2,he,2);
- h a , 3 t e m p = A g g r e g a t i o n ( h a , 3 , h b , 3 , h c , 3 , h d , 3 , h e , 3 ) h^{temp}_{a,3} = Aggregation(h_{a,3},h_{b,3},h_{c,3},h_{d,3},h_{e,3}) ha,3temp=Aggregation(ha,3,hb,3,hc,3,hd,3,he,3);
- Applying a nonlinear function to generate the output features(得到 [ h a , 1 ′ h a , 2 ′ ] \begin{bmatrix}h^{'}_{a,1}\\h^{'}_{a,2}\end{bmatrix} [ha,1′ha,2′]):
σ ( W 2 , 3 × [ h a , 1 t e m p h a , 2 t e m p h a , 3 t e m p ] ) = σ ( [ w 1 , 1 w 1 , 2 w 1 , 3 w 2 , 1 w 2 , 2 w 2 , 3 ] × [ h a , 1 t e m p h a , 2 t e m p h a , 3 t e m p ] ) = [ h a , 1 ′ h a , 2 ′ ] \operatorname{σ}\left(W_{2,3} × \begin{bmatrix}h^{temp}_{a,1}\\h^{temp}_{a,2}\\h^{temp}_{a,3}\end{bmatrix}\right) = \operatorname{σ}\left(\begin{bmatrix}w_{1,1} & w_{1,2} & w_{1,3}\\w_{2,1} & w_{2,2} & w_{2,3}\end{bmatrix} × \begin{bmatrix}h^{temp}_{a,1}\\h^{temp}_{a,2}\\h^{temp}_{a,3}\end{bmatrix}\right) =\begin{bmatrix}h^{'}_{a,1}\\h^{'}_{a,2}\end{bmatrix} σ⎝⎛W2,3×⎣⎡ha,1tempha,2tempha,3temp⎦⎤⎠⎞=σ⎝⎛[w1,1w2,1w1,2w2,2w1,3w2,3]×⎣⎡ha,1tempha,2tempha,3temp⎦⎤⎠⎞=[ha,1′ha,2′]
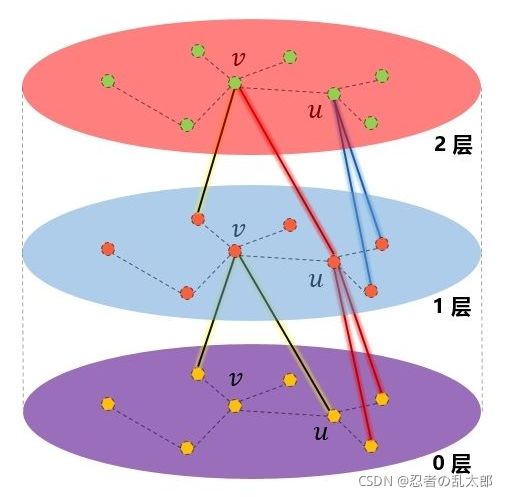
4、“图卷积模型”的层(Layer)【一般用2~3层】
GCN 的层类似于CNN里的卷积层,Complete GCN consists of multiple convolutional layers。
- Nodes have embeddings at each layer;
- Model can be arbitrary depth;
- Layer-0 embedding of node u u u is its input feature, i.e. x u x_u xu;
- Layer- embedding of node u u u gets information from nodes that are hops away
二、“图卷积模型”框架设计流程
GNN(GCN/GraphSAGE/GAT…)通用设计流程
- 定义一个邻域节点汇聚函数 A g g r e g a t i o n ( N v ) \color{D60595}{Aggregation(\mathcal{N}_v) } Aggregation(Nv)(Define a neighborhood aggregation function);
- 定义一个损失函数 L ( z v ) \color{D60595}{\mathcal{L}(\textbf{z}_v)} L(zv)(Define a loss function on the embeddings);
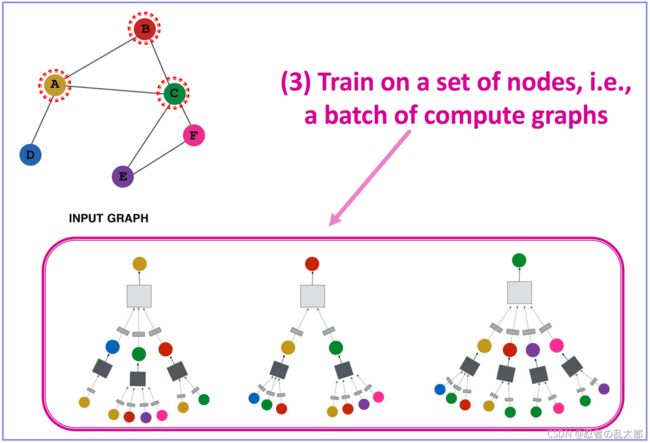
- 训练节点(Train on a set of nodes, i.e.,a batch of compute graphs),来学习模型参数 θ \color{D60595}{\mathcal{θ}} θ;
- 根据优化后的模型(参数 θ \color{D60595}{\mathcal{θ}} θ),输入某个节点(在归纳式GNN中,可以是未见过的新图的节点)的特征值 x \textbf{x} x,输出该节点的节点向量 z v \color{D60595}{\textbf{z}_v} zv;
三、“图卷积模型”通用算法细节
1、前向传播(消息传递聚合):邻居节点信息聚合(Neighborhood Aggregation)
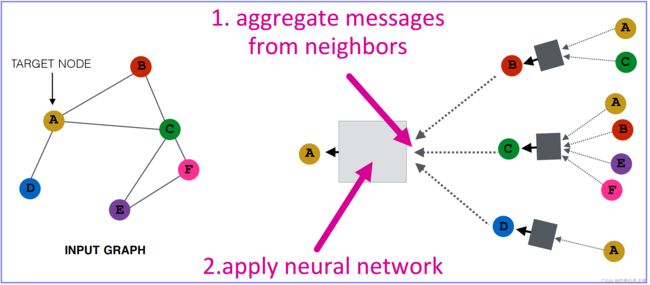
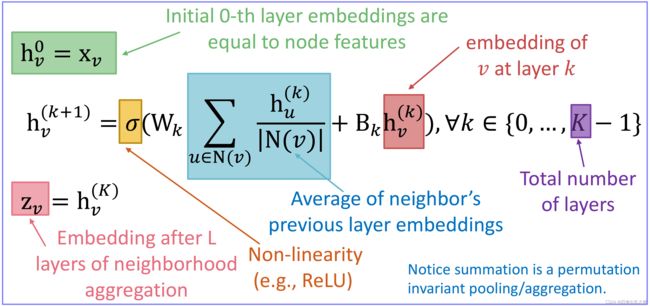
由于在图中顶点的邻居是天然无序的,所以我们希望构造出的聚合函数是对称的(即改变输入的顺序,函数的输出结果不变),同时具有较高的表达能力。
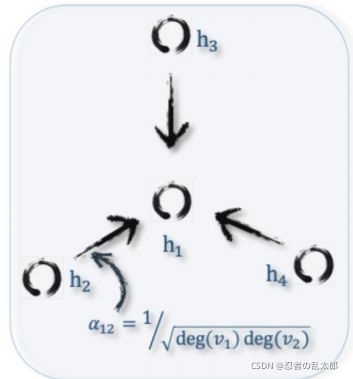
其中汇聚邻域节点信息的聚合函数 AGG ( { h u k , ∀ u ∈ N ( v ) } ) \operatorname{AGG}(\{\textbf{h}_u^{k}, ∀u∈N(v)\}) AGG({huk,∀u∈N(v)}) 可以有多种形式,GCN、GraphSAGE、GAT的不同之处就在于 AGG \operatorname{AGG} AGG 的不同:
- GCN模型:
AGG = ∑ u ∈ N ( v ) h u k ∣ N ( v ) ∣ \begin{aligned}\operatorname{AGG} = \sum_{u∈N(v)}\dfrac{\textbf{h}_u^{k}}{|N(v)|}\end{aligned} AGG=u∈N(v)∑∣N(v)∣huk - GraphSAGE模型(3种) :
- Mean:
AGG = ∑ u ∈ N ( v ) h u k ∣ N ( v ) ∣ \begin{aligned}\operatorname{AGG} = \sum_{u∈N(v)}\dfrac{\textbf{h}_u^{k}}{|N(v)|}\end{aligned} AGG=u∈N(v)∑∣N(v)∣huk - Pool:Transform neighbor vectors(矩阵 Q \textbf{Q} Q,可以做维度变换) and apply symmetric vector function(element-wise mean/max pooling)。
AGG = pool ( { Q h u k , ∀ u ∈ N ( v ) } ) \begin{aligned}\operatorname{AGG} = \operatorname{pool}(\{\textbf{Q}\textbf{h}_u^{k}, ∀u∈N(v)\})\end{aligned} AGG=pool({Qhuk,∀u∈N(v)}) - LSTM:Apply LSTM to random permutation of neighbors【公式中的 π π π表示随机排列,消除节点输入LSTM的顺序的影响(邻域中的节点不应该有顺序)】.
AGG = LSTM ( { h u k , ∀ u ∈ π ( N ( v ) ) } ) \begin{aligned}\operatorname{AGG} = \operatorname{LSTM}(\{\textbf{h}_u^{k}, ∀u∈π(N(v))\})\end{aligned} AGG=LSTM({huk,∀u∈π(N(v))})
- Mean:
- GAT模型:
AGG = Attention ( { h u k , ∀ u ∈ N ( v ) } ) \begin{aligned}\operatorname{AGG} = \operatorname{Attention}(\{\textbf{h}_u^{k}, ∀u∈N(v)\})\end{aligned} AGG=Attention({huk,∀u∈N(v)})
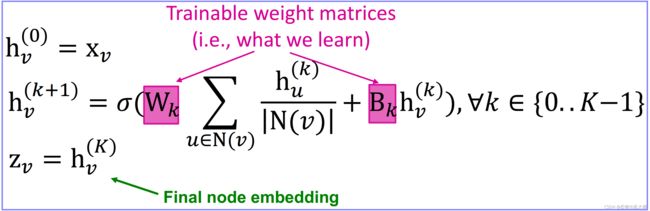
2、反向传播
将最后一层得到的各个节点的 Embedding喂给损失函数,利用梯度下降算法来训练参数。
- k k k:表示第 k k k 层;
- h v k h_v^k hvk: the hidden representation of node at layer k;
- W k W_k Wk: weight matrix for neighborhood aggregation,同一层的所有节点的 W W W 共享,不同层的 W W W 不同(待训练参数);
- B k B_k Bk: weight matrix for transforming hidden vector of self(待训练参数);
四、“图卷积模型”通用训练方式
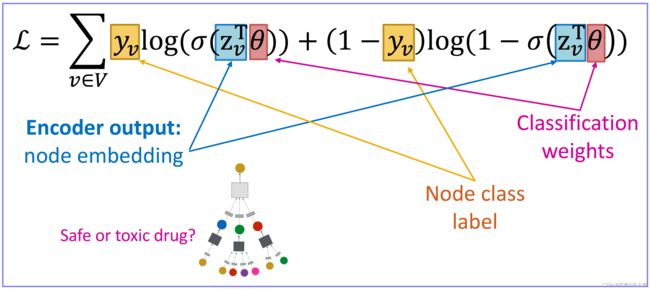
如何训练GNN模型来获得各个节点的Embedding?需要为 Embedding定义一个损失函数(Need to define a loss function on the embeddings.)
1、无监督训练【附近的节点具有相似的Embedding表示,不同节点的Embedding表示不同(负采样)】
没有节点标签,利用图的拓扑结构本身作为监督(Use the graph structure as the supervision):相似的节点具有相似的Embedding(“Similar” nodes have similar embeddings)
L = ∑ z u , z v C E ( y u , v , D E C ( z u , z v ) ) \color{red}{\mathcal{L}=\sum_{z_u,z_v}CE\left(y_{u,v},DEC(z_u,z_v)\right)} L=zu,zv∑CE(yu,v,DEC(zu,zv))
- y u , v = S i m i l a r i t y ( u , v ) = 1 y_{u,v} = Similarity(u,v)= 1 yu,v=Similarity(u,v)=1 when node u and v are similar;
- C E CE CE:表示交叉熵函数;
- D E C DEC DEC:表示Decoder(比如内积)
采用负采样后,与Word2vec模型的损失函数一样:
1.1 Encoder
Encoder: maps each node to a low-dimensional vector
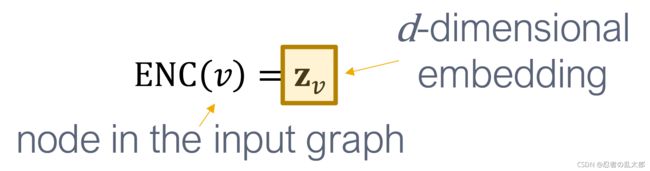
1.2 Similarity function
Similarity function:度量原始网络中节点间的相似性【measure of similarity in the original network】。
Similarity of node u u u and v v v in the original network:
S i m i l a r i t y ( u , v ) Similarity(u,v) Similarity(u,v)
常用的度量原始网络中节点间的相似性 S i m i l a r i t y ( u , v ) Similarity(u,v) Similarity(u,v)的方法:
- Naïve: similar if two nodes are connected(一阶相似度);
- Neighborhood overlap (二阶相似度);
- Random walk approaches (套用Word2vec中的Skip2gram算法);
1.3 Decoder
Decoder:从嵌入到相似性分数的映射【maps from embeddings to the similarity score 】
Similarity of the embedding z u 、 z v z_u、z_v zu、zv:
D E C ( z u T ⋅ z v ) DEC(z_u^T·z_v) DEC(zuT⋅zv)
1.4 优化
Optimize the parameters of the encoder so that:
S i m i l a r i t y ( u , v ) ≈ D E C ( z u T ⋅ z v ) Similarity(u,v)≈DEC(z_u^T·z_v) Similarity(u,v)≈DEC(zuT⋅zv)
z u T ⋅ z v z_u^T·z_v zuT⋅zv:dot product between node embeddings
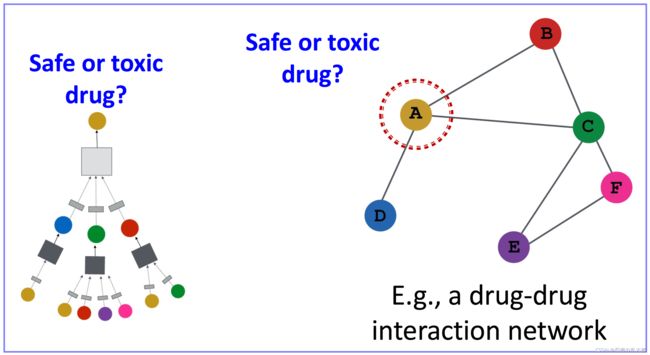
2、有监督训练(比如:节点分类)
Directly train the model for a supervised task (e.g., node classification)
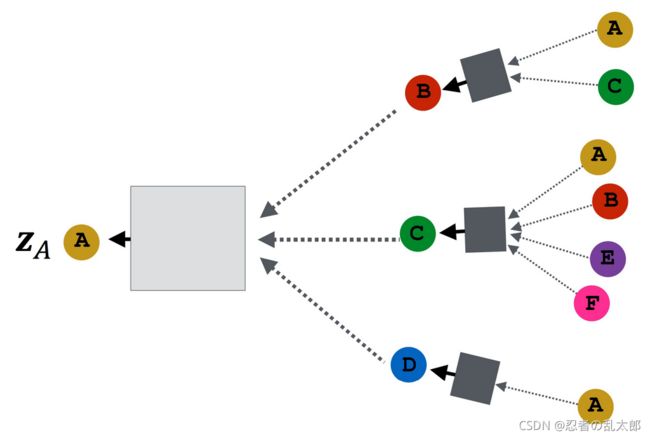
五、“图卷积模型”通用算法(借鉴GranphSAGE的流程)
- K K K:表示神经网络一共有多少层;每一层的 W k 、 AGGREGATE k \operatorname{W}^k、\operatorname{AGGREGATE}_k Wk、AGGREGATEk 都不一样;
- h 0 ← x v \textbf{h}^0\leftarrow \textbf{x}_v h0←xv:表示在第 0 0 0 层,将图的原始属性特征 x v \textbf{x}_v xv 赋值给 h 0 \textbf{h}^0 h0;
- h N ( v ) k ← AGGREGATE k ( { h u k − 1 , ∀ u ∈ N ( v ) } ) \textbf{h}^k_{\mathcal{N_(v)}}\leftarrow \operatorname{AGGREGATE}_k(\{\textbf{h}_u^{k-1}, ∀u∈N(v)\}) hN(v)k←AGGREGATEk({huk−1,∀u∈N(v)}):表示在第 k k k 层神经网络中,对节点 v v v 的邻域所有节点在 k − 1 k-1 k−1 层的节点向量做一次聚合操作,得到邻域所有节点在第 k k k 层的的聚合结果;
- h v k ← σ ( W k ⋅ C O N C A T ( h v k − 1 , h N ( v ) k ) ) \textbf{h}_v^{k} \leftarrow σ(\textbf{W}^k·\operatorname{CONCAT(\textbf{h}_v^{k-1},\textbf{h}^k_{\mathcal{N_(v)}})}) hvk←σ(Wk⋅CONCAT(hvk−1,hN(v)k)):表示将得到的第 k k k 层的邻域所有节点的聚合结果 h N ( v ) k \textbf{h}^k_{\mathcal{N_(v)}} hN(v)k 与本节点 v v v 的上一层的结果 h v k − 1 \textbf{h}_v^{k-1} hvk−1进行拼接,然后经过一个全连接网络,非线性函数 σ σ σ,得到本节点 v v v 在 k k k 层的节点向量表示: h v k \textbf{h}_v^{k} hvk ;
- h v k ← h v k / ∣ ∣ h v k ∣ ∣ 2 , ∀ v ∈ V \textbf{h}_v^{k} \leftarrow \textbf{h}_v^{k}/||\textbf{h}_v^{k}||_2,∀v∈\mathcal{V} hvk←hvk/∣∣hvk∣∣2,∀v∈V:表示进行归一化操作;
- z v ← h v K , ∀ v ∈ V \textbf{z}_v \leftarrow \textbf{h}_v^{K},∀v∈\mathcal{V} zv←hvK,∀v∈V:表示将最后一层神经网络得到的节点向量作为最终得到的节点向量,此 z v \textbf{z}_v zv 可以喂给损失函数来进行优化;
六、GCN、GraphSAGE、GAT联系与区别
我们可以发现就本质而言,GCN、GraphSAGE、GAT都是将邻居节点的特征聚合到中心节点上,其实就是一种聚合(aggregate)运算,利用graph上的local stationary学习新的顶点特征表达。
GCN、GraphSAGE、GAT都是一种局部网络。因此,(相比于GNN或GGNN等网络)训练GCN、GraphSAGE、GAT模型无需了解整个图结构,只需知道每个节点的邻节点即可。
不同的是GCN用的是拉普拉斯矩阵,而GAT用的是注意力系数,在一定程度上来说,GAT会更强,因为GAT很好的将顶点的特征之间的相关性融入到了模型之中。相比于GCN,每个节点的重要性可以是不同的,因此,GAT具有更强的表示能力。
X = [ x ⃗ 1 x ⃗ 2 x ⃗ 3 ] = [ x 11 x 12 x 21 x 22 x 31 x 32 ] H 0 = X H l = [ h ⃗ 1 h ⃗ 2 h ⃗ 3 ] = [ h 11 h 12 h 21 h 22 h 31 h 32 ] X=\left[\begin{array}{ll}\vec{x}_1 \\\vec{x}_2\\ \vec{x}_3 \end{array}\right]=\left[\begin{array}{ll}x_{11} & x_{12} \\x_{21} & x_{22} \\ x_{31} & x_{32} \end{array}\right] \quad H^0=X \quad H^l=\left[\begin{array}{ll}\vec{h}_1 \\\vec{h}_2\\ \vec{h}_3 \end{array}\right]=\left[\begin{array}{ll}h_{11} & h_{12} \\h_{21} & h_{22} \\ h_{31} & h_{32} \end{array}\right] X=⎣⎡x1x2x3⎦⎤=⎣⎡x11x21x31x12x22x32⎦⎤H0=XHl=⎣⎢⎡h1h2h3⎦⎥⎤=⎣⎡h11h21h31h12h22h32⎦⎤
W = [ w 11 w 12 w 13 w 14 w 21 w 22 w 23 w 24 ] W=\left[\begin{array}{ll} w_{11} & w_{12} & w_{13} & w_{14} \\ w_{21} & w_{22} & w_{23} & w_{24}\end{array}\right] W=[w11w21w12w22w13w23w14w24]
A = [ a 11 a 12 0 0 a 22 a 23 0 0 a 33 ] A=\left[\begin{array}{lll} a_{11} & a_{12} & 0 \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{array}\right] A=⎣⎡a1100a12a2200a23a33⎦⎤
其中:
- X ⃗ \vec{X} X 表示图的各个节点的Feature数据;
- H l H^l Hl:表示第 l l l 层 Graph Attentional Layer(类似于CNN的第 l l l 层卷积层);
- h ⃗ i \vec{h}_i hi 表示各个节点的Embedding, h ⃗ 1 = ( h 11 , h 12 ) \vec{h}_1=(h_{11} , h_{12}) h1=(h11,h12) 表示节点1用一个2维向量来表示,一般会用128维来表示;
- W W W:图中的所有节点都共用 W W W,可以用来升维或降维(将每个节点的 h ⃗ i \vec{h}_i hi由2维升为4维);
- w i j w_{ij} wij:表示节点的各个维度的权重系数(模型要学习的参数);
- 各个节点的区别就在于Feature不一样,即: H H H不一样;
- A A A 表示聚合函数;
H W = [ y 1 y 2 y 3 ] = [ w 11 h 11 + w 21 h 12 w 12 h 11 + w 22 h 12 w 13 h 11 + w 23 h 12 w 14 h 11 + w 24 h 12 w 11 h 21 + w 21 h 22 w 12 h 21 + w 22 h 22 w 13 h 21 + w 23 h 22 w 14 h 21 + w 24 h 22 w 11 h 31 + w 21 h 32 w 12 h 31 + w 22 h 32 w 13 h 31 + w 23 h 32 w 14 h 31 + w 24 h 32 ] \mathrm{HW}=\left[\begin{array}{l} \boldsymbol{y}_{1} \\ \boldsymbol{y}_{2} \\ \boldsymbol{y}_{3} \end{array}\right]=\left[\begin{array}{ll} w_{11} h_{11}+w_{21} h_{12} & w_{12} h_{11}+w_{22} h_{12} & w_{13} h_{11}+w_{23} h_{12} & w_{14} h_{11}+w_{24} h_{12} \\ w_{11} h_{21}+w_{21} h_{22} & w_{12} h_{21}+w_{22} h_{22} & w_{13} h_{21}+w_{23} h_{22} & w_{14} h_{21}+w_{24} h_{22} \\ w_{11} h_{31}+w_{21} h_{32} & w_{12} h_{31}+w_{22} h_{32} & w_{13} h_{31}+w_{23} h_{32} & w_{14} h_{31}+w_{24} h_{32} \end{array}\right] HW=⎣⎡y1y2y3⎦⎤=⎣⎡w11h11+w21h12w11h21+w21h22w11h31+w21h32w12h11+w22h12w12h21+w22h22w12h31+w22h32w13h11+w23h12w13h21+w23h22w13h31+w23h32w14h11+w24h12w14h21+w24h22w14h31+w24h32⎦⎤
H l + 1 = A H l W = [ a 11 ( w 11 h 11 + w 21 h 12 ) + a 12 ( w 11 h 21 + w 21 h 22 ) a 11 ( w 12 h 11 + w 22 h 12 ) + a 12 ( w 12 h 21 + w 22 h 22 ) a 11 ( w 13 h 11 + w 23 h 12 ) + a 12 ( w 13 h 21 + w 23 h 22 ) a 11 ( w 14 h 11 + w 24 h 12 ) + a 12 ( w 14 h 21 + w 24 h 22 ) a 22 ( w 11 h 21 + w 21 h 22 ) + a 23 ( w 11 h 31 + w 21 h 32 ) a 22 ( w 12 h 21 + w 22 h 22 ) + a 23 ( w 12 h 31 + w 22 h 32 ) a 22 ( w 13 h 21 + w 23 h 22 ) + a 23 ( w 13 h 31 + w 23 h 32 ) a 22 ( w 14 h 21 + w 24 h 22 ) + a 23 ( w 14 h 31 + w 24 h 32 ) a 33 ( w 11 h 31 + w 21 h 32 ) a 33 ( w 12 h 31 + w 22 h 32 ) a 33 ( w 13 h 31 + w 23 h 32 ) a 33 ( w 14 h 31 + w 24 h 32 ) ] H^{l+1}=AH^lW=\left[\begin{array}{cc} a_{11}(w_{11} h_{11}+w_{21} h_{12})+a_{12}(w_{11} h_{21}+w_{21} h_{22}) & a_{11}(w_{12} h_{11}+w_{22} h_{12})+a_{12}(w_{12} h_{21}+w_{22} h_{22}) & a_{11}(w_{13} h_{11}+w_{23} h_{12})+a_{12}(w_{13} h_{21}+w_{23} h_{22}) & a_{11}(w_{14} h_{11}+w_{24} h_{12})+a_{12}(w_{14} h_{21}+w_{24} h_{22}) \\ a_{22}(w_{11} h_{21}+w_{21} h_{22})+a_{23}(w_{11} h_{31}+w_{21} h_{32}) & a_{22}(w_{12} h_{21}+w_{22} h_{22})+a_{23}(w_{12} h_{31}+w_{22} h_{32}) & a_{22}(w_{13} h_{21}+w_{23} h_{22})+a_{23}(w_{13} h_{31}+w_{23} h_{32})& a_{22}(w_{14} h_{21}+w_{24} h_{22})+a_{23}(w_{14} h_{31}+w_{24} h_{32}) \\ a_{33(}w_{11} h_{31}+w_{21} h_{32}) & a_{33}(w_{12} h_{31}+w_{22} h_{32}) & a_{33}(w_{13} h_{31}+w_{23} h_{32}) & a_{33}(w_{14} h_{31}+w_{24} h_{32}) \end{array}\right] Hl+1=AHlW=⎣⎡a11(w11h11+w21h12)+a12(w11h21+w21h22)a22(w11h21+w21h22)+a23(w11h31+w21h32)a33(w11h31+w21h32)a11(w12h11+w22h12)+a12(w12h21+w22h22)a22(w12h21+w22h22)+a23(w12h31+w22h32)a33(w12h31+w22h32)a11(w13h11+w23h12)+a12(w13h21+w23h22)a22(w13h21+w23h22)+a23(w13h31+w23h32)a33(w13h31+w23h32)a11(w14h11+w24h12)+a12(w14h21+w24h22)a22(w14h21+w24h22)+a23(w14h31+w24h32)a33(w14h31+w24h32)⎦⎤
GCN、GraphSAGE、GAT的不同之处在于有着不同的节点聚合方式(Aggregation rule:将邻域所有节点的信息汇聚到自身的方式)【由第 l l l 层的节点向量更新出第 l + 1 l+1 l+1 层的节点向量】:
1、GCN的聚合方式
A G C N = [ 1 1 0 0 1 1 0 0 1 ] A^{GCN}=\left[\begin{array}{lll} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array}\right] \quad AGCN=⎣⎡100110011⎦⎤
GCN使用的是 A G C N A^{GCN} AGCN【单层GCN(下面的公式忽略激活函数)】【Weights in average depends on degree of neighbouring nodes】:
H l + 1 = A G C N H l W = [ ( w 11 h 11 + w 21 h 12 ) + ( w 11 h 21 + w 21 h 22 ) ( w 12 h 11 + w 22 h 12 ) + ( w 12 h 21 + w 22 h 22 ) ( w 13 h 11 + w 23 h 12 ) + ( w 13 h 21 + w 23 h 22 ) ( w 14 h 11 + w 24 h 12 ) + ( w 14 h 21 + w 24 h 22 ) ( w 11 h 21 + w 21 h 22 ) + ( w 11 h 31 + w 21 h 32 ) ( w 12 h 21 + w 22 h 22 ) + ( w 12 h 31 + w 22 h 32 ) ( w 13 h 21 + w 23 h 22 ) + ( w 13 h 31 + w 23 h 32 ) ( w 14 h 21 + w 24 h 22 ) + ( w 14 h 31 + w 24 h 32 ) w 11 h 31 + w 21 h 32 w 12 h 31 + w 22 h 32 w 13 h 31 + w 23 h 32 w 14 h 31 + w 24 h 32 ] H^{l+1}=A^{GCN}H^lW=\left[\begin{array}{cc} (w_{11} h_{11}+w_{21} h_{12})+(w_{11} h_{21}+w_{21} h_{22}) & (w_{12} h_{11}+w_{22} h_{12})+(w_{12} h_{21}+w_{22} h_{22}) & (w_{13} h_{11}+w_{23} h_{12})+(w_{13} h_{21}+w_{23} h_{22})& (w_{14} h_{11}+w_{24} h_{12})+(w_{14} h_{21}+w_{24} h_{22}) \\ (w_{11} h_{21}+w_{21} h_{22})+(w_{11} h_{31}+w_{21} h_{32}) & (w_{12} h_{21}+w_{22} h_{22})+(w_{12} h_{31}+w_{22} h_{32}) & (w_{13} h_{21}+w_{23} h_{22})+(w_{13} h_{31}+w_{23} h_{32}) & (w_{14} h_{21}+w_{24} h_{22})+(w_{14} h_{31}+w_{24} h_{32}) \\ w_{11} h_{31}+w_{21} h_{32} & w_{12} h_{31}+w_{22} h_{32} & w_{13} h_{31}+w_{23} h_{32} & w_{14} h_{31}+w_{24} h_{32} \end{array}\right] Hl+1=AGCNHlW=⎣⎡(w11h11+w21h12)+(w11h21+w21h22)(w11h21+w21h22)+(w11h31+w21h32)w11h31+w21h32(w12h11+w22h12)+(w12h21+w22h22)(w12h21+w22h22)+(w12h31+w22h32)w12h31+w22h32(w13h11+w23h12)+(w13h21+w23h22)(w13h21+w23h22)+(w13h31+w23h32)w13h31+w23h32(w14h11+w24h12)+(w14h21+w24h22)(w14h21+w24h22)+(w14h31+w24h32)w14h31+w24h32⎦⎤
2、GAT的聚合方式
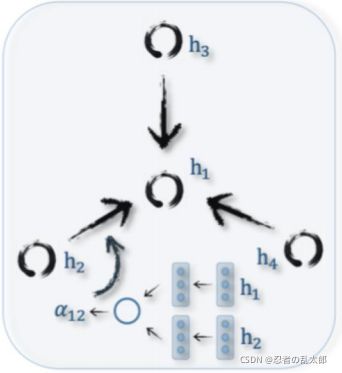
A G A T = [ α 11 α 12 0 0 α 22 α 23 0 0 α 33 ] A^{GAT}=\left[\begin{array}{lll} α_{11} & α_{12} & 0 \\ 0 & α_{22} & α_{23} \\ 0 & 0 & α_{33} \end{array}\right] AGAT=⎣⎡α1100α12α2200α23α33⎦⎤
GAT使用的是 A G A T A^{GAT} AGAT【GAT使用 self-attention为每个邻节点分配权重(下面的公式忽略激活函数)】【Weights computed by a self-attention mechanism based on node features】:
H l + 1 = A G A T H l W = [ α 11 ( w 11 h 11 + w 21 h 12 ) + α 12 ( w 11 h 21 + w 21 h 22 ) α 11 ( w 12 h 11 + w 22 h 12 ) + α 12 ( w 12 h 21 + w 22 h 22 ) α 11 ( w 13 h 11 + w 23 h 12 ) + α 12 ( w 13 h 21 + w 23 h 22 ) α 11 ( w 14 h 11 + w 24 h 12 ) + α 12 ( w 14 h 21 + w 24 h 22 ) α 22 ( w 11 h 21 + w 21 h 22 ) + α 23 ( w 11 h 31 + w 21 h 32 ) α 22 ( w 12 h 21 + w 22 h 22 ) + α 23 ( w 12 h 31 + w 22 h 32 ) α 22 ( w 13 h 21 + w 23 h 22 ) + α 23 ( w 13 h 31 + w 23 h 32 ) α 22 ( w 14 h 21 + w 24 h 22 ) + α 23 ( w 14 h 31 + w 24 h 32 ) α 33 ( w 11 h 31 + w 21 h 32 ) α 33 ( w 12 h 31 + w 22 h 32 ) α 33 ( w 13 h 31 + w 23 h 32 ) α 33 ( w 14 h 31 + w 24 h 32 ) ] H^{l+1}=A^{GAT}H^lW=\left[\begin{array}{cc} α_{11}(w_{11} h_{11}+w_{21} h_{12})+α_{12}(w_{11} h_{21}+w_{21} h_{22}) & α_{11}(w_{12} h_{11}+w_{22} h_{12})+α_{12}(w_{12} h_{21}+w_{22} h_{22}) & α_{11}(w_{13} h_{11}+w_{23} h_{12})+α_{12}(w_{13} h_{21}+w_{23} h_{22}) & α_{11}(w_{14} h_{11}+w_{24} h_{12})+α_{12}(w_{14} h_{21}+w_{24} h_{22}) \\ α_{22}(w_{11} h_{21}+w_{21} h_{22})+α_{23}(w_{11} h_{31}+w_{21} h_{32}) & α_{22}(w_{12} h_{21}+w_{22} h_{22})+α_{23}(w_{12} h_{31}+w_{22} h_{32}) & α_{22}(w_{13} h_{21}+w_{23} h_{22})+α_{23}(w_{13} h_{31}+w_{23} h_{32})& α_{22}(w_{14} h_{21}+w_{24} h_{22})+α_{23}(w_{14} h_{31}+w_{24} h_{32}) \\ α_{33(}w_{11} h_{31}+w_{21} h_{32}) & α_{33}(w_{12} h_{31}+w_{22} h_{32}) & α_{33}(w_{13} h_{31}+w_{23} h_{32}) & α_{33}(w_{14} h_{31}+w_{24} h_{32}) \end{array}\right] Hl+1=AGATHlW=⎣⎡α11(w11h11+w21h12)+α12(w11h21+w21h22)α22(w11h21+w21h22)+α23(w11h31+w21h32)α33(w11h31+w21h32)α11(w12h11+w22h12)+α12(w12h21+w22h22)α22(w12h21+w22h22)+α23(w12h31+w22h32)α33(w12h31+w22h32)α11(w13h11+w23h12)+α12(w13h21+w23h22)α22(w13h21+w23h22)+α23(w13h31+w23h32)α33(w13h31+w23h32)α11(w14h11+w24h12)+α12(w14h21+w24h22)α22(w14h21+w24h22)+α23(w14h31+w24h32)α33(w14h31+w24h32)⎦⎤
参考资料:
从GNN到GCN(1)–传统GCN和基于空域的MPNN及GraphSage
如何通俗易懂地解释卷积?
从CNN到GCN的联系与区别——GCN从入门到精(fang)通(qi)
技术思辨:GCN和CNN到底有什么差别?
CNN与GCN的区别、联系及融合
GCN、GAT、GraphSAGE的优势很明显,想问一下它们分别有什么缺点?
GCN、GAT、GraphSAGE 的优势很明显,想问一下它们分别有什么缺点?
如何通俗易懂地解释卷积?
(三)图神经网络消息传递