第二周.DGL初体验
文章目录
- Deep Graph Library基本介绍
- 节点分类
-
- 加载数据集
- 创建GCN
- 训练GCN
- 图的基本操作 based on DGL
-
- 点和边的特征表示
- 查询图结构信息
- 图的切割
- 保存和加载图
- 消息传递框架Message passing
-
- 自定义SAGEConv
- 定义GraphSAGE模型
- 训练
- GraphSAGE的变形
-
- 带权GraphSAGE卷积层
- 定义模型
- 训练
- 边预测
-
- 预处理
- 定义GraphSAGE模型
- 正样本图+负样本图
- 训练
本文内容整理自深度之眼《GNN核心能力培养计划》,第一周是GNN的理论知识复习,基本在GNN论文带读中有涵盖,就不写了。从第二周开始。
https://docs.dgl.ai/guide_cn/index.html
https://github.com/dmlc/dgl/tree/master/tutorials/blitz
Deep Graph Library基本介绍
是亚马逊开发的GNN深度学习框架,在复现模型,简化搭建自己的模型上有很好的优势,也是我们选用这个框架作为本次课程学习内容的主要原因。本周通过几个简单例子先对DGL简单的上手一下。
环境要求:
Python 3.7
PyTorch 1.8.1
DGL 0.6.1
GPU没有也木有关系
安装我直接用的pip install就ok,基础环境我用conda复制了一份base,因为要用jupyter。
conda create -n env_name --clone base
然后装torch和DGL(安装说明看这里:https://github.com/dmlc/dgl)
导入库没报错就ok
import dgl
import torch
import torch.nn as nn
import torch.nn.functional as F
节点分类
用DGL自带的Cora数据集,关于这个数据集的介绍看这里。
This tutorial will show how to build such a GNN for semi-supervised node classification with only a small number of labels on the Cora dataset, a citation network with papers as nodes and citations as edges. The task is to predict the category of a given paper. Each paper node contains a word count vector as its features, normalized so that they sum up to one, as described in Section 5.2 of Semi-Supervised Classification with Graph Convolutional Networks
文章是节点,引用是边,节点的特征表示用的word count vector(要有归一化操作)
加载数据集
import dgl.data
# networkx
dataset = dgl.data.CoraGraphDataset()
print('Number of categories:', dataset.num_classes)
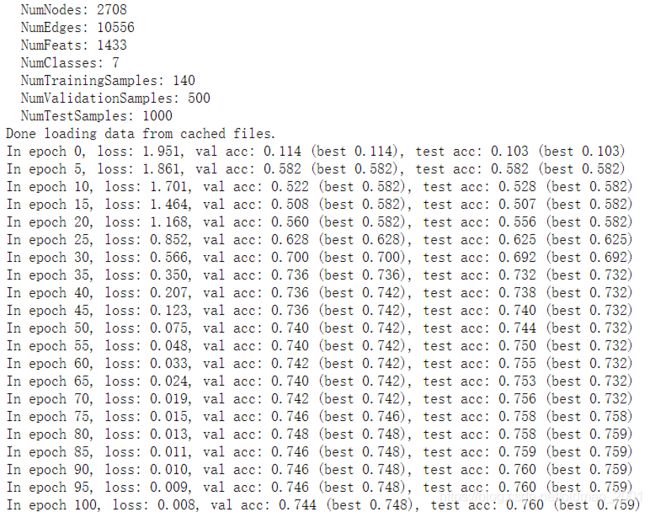
打印结果:
Downloading C:\Users\mhq.dgl\cora_v2.zip from https://data.dgl.ai/dataset/cora_v2.zip…
Extracting file to C:\Users\mhq.dgl\cora_v2
Finished data loading and preprocessing.
NumNodes: 2708#节点数量
NumEdges: 10556#边数量
NumFeats: 1433#节点特征维度
NumClasses: 7#节点分类
NumTrainingSamples: 140#训练集
NumValidationSamples: 500#验证集
NumTestSamples: 1000#测试集
Done saving data into cached files.
Number of categories: 7
DGL的数据集对象可以包含多个图,但是Cora数据集中只有一个图,因此图的读取为:
g = dataset[0]
在g这个图数据集对象中,节点特征和边特征分别在ndata和edata属性中,但是所有的节点按上面的训练集、验证集、测试集进行了划分,因此在ndata中用不同的mask代表该节点属于哪个集合:
train_mask: A boolean tensor indicating whether the node is in the training set.
val_mask: A boolean tensor indicating whether the node is in the validation set.
test_mask: A boolean tensor indicating whether the node is in the test set.
除了mask信息,还有标签和特征信息:
label: The ground truth node category.
feat: The node features.
用代码把这些信息打印出来看看
print('Node features')
print(g.ndata)
print('Edge features')
print(g.edata)
如下图所示,红色部分是mask,train_mask长度是2708,它的前面140位都是true,后面都是false,蓝色部分是label,代表每个节点的分类(ground truth),绿色的是一个二维矩阵,每行是每个节点的特征表示。
边特征信息这里没有,是空的。

创建GCN
弄一个两层GCN,如果要创建更多层的模型可以堆叠dgl.nn.GraphConv
如果是用别的聚合方式可以用别的接口。
from dgl.nn import GraphConv
class GCN(nn.Module):
def __init__(self, in_feats, h_feats, num_classes):#初始化
super(GCN, self).__init__()
self.conv1 = GraphConv(in_feats, h_feats)#第一层in_feats的输入维度,这里是1433,h_feats是第一层的输出维度
self.conv2 = GraphConv(h_feats, num_classes)#第二层,h_feats是第一层的输出也就是第二层的输入,num_classes是节点的分类数量
def forward(self, g, in_feat):#前向传播过程
h = self.conv1(g, in_feat)#第一层卷积吃图数据,输入维度,对应的卷积操作是GCN原文公式的AXW(红色部分)
h = F.relu(h)#黄色部分
h = self.conv2(g, h)#蓝色部分
return h
# Create the model with given dimensions
#model = GCN(g.ndata['feat'].shape[1], 16, dataset.num_classes)
#g.ndata['feat'].shape[1]是特征矩阵([2708, 1433])的第二个的维度,上面这句代码不用写这里,下面有。。。
训练GCN
def train(g, model):
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
best_val_acc = 0
best_test_acc = 0
#取出各种词典
features = g.ndata['feat']
labels = g.ndata['label']
train_mask = g.ndata['train_mask']
val_mask = g.ndata['val_mask']
test_mask = g.ndata['test_mask']
for e in range(100):#训练100个epoch
# Forward
logits = model(g, features)
# Compute prediction
pred = logits.argmax(1)
# Compute loss
# Note that you should only compute the losses of the nodes in the training set.
#利用训练数据集来计算loss,注意这里mask的使用
loss = F.cross_entropy(logits[train_mask], labels[train_mask])
# Compute accuracy on training/validation/test
train_acc = (pred[train_mask] == labels[train_mask]).float().mean()
val_acc = (pred[val_mask] == labels[val_mask]).float().mean()
test_acc = (pred[test_mask] == labels[test_mask]).float().mean()
# Save the best validation accuracy and the corresponding test accuracy.
#保存验证集准确率和测试集准确率
if best_val_acc < val_acc:
best_val_acc = val_acc
best_test_acc = test_acc
# Backward
optimizer.zero_grad()
loss.backward()
optimizer.step()
if e % 5 == 0:
print('In epoch {}, loss: {:.3f}, val acc: {:.3f} (best {:.3f}), test acc: {:.3f} (best {:.3f})'.format(
e, loss, val_acc, best_val_acc, test_acc, best_test_acc))
model = GCN(g.ndata['feat'].shape[1], 16, dataset.num_classes)
train(g, model)
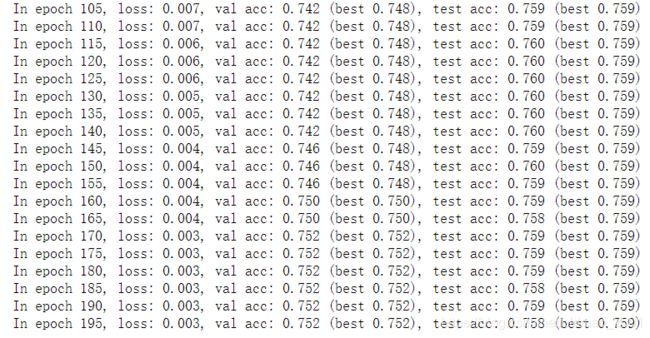
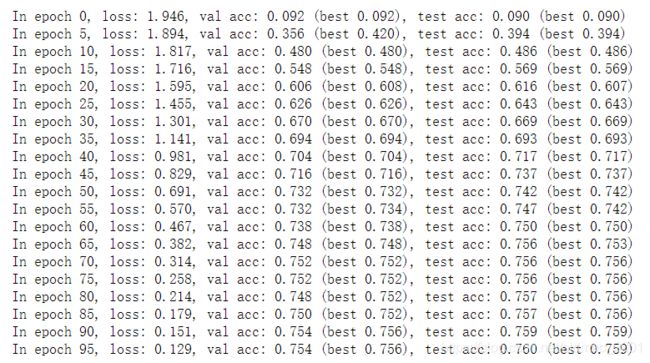
结果:
如果要使用GPU,可以使用to函数把数据丢进显存里面
g = g.to('cuda') model = GCN(g.ndata['feat'].shape[1], 16, dataset.num_classes).to('cuda') train(g, model)
图的基本操作 based on DGL
DGL中默认是有向图,因此在创建图的时候,除了要指定节点之外,指定边的时候节点的顺序是不能颠倒的(源节点→目标节点)。
import dgl
import numpy as np
import torch
#这里将邻接矩阵的源节点和目标节点分别拿出来,最后给出节点数量(这个参数在所有节点都在源节点和目标节点集合里面的时候可以省略)
g = dgl.graph(([0, 0, 0, 0, 0], [1, 2, 3, 4, 5]), num_nodes=6)
# Equivalently, PyTorch LongTensors also work.
g = dgl.graph((torch.LongTensor([0, 0, 0, 0, 0]), torch.LongTensor([1, 2, 3, 4, 5])), num_nodes=6)
# You can omit the number of nodes argument if you can tell the number of nodes from the edge list alone.
g = dgl.graph(([0, 0, 0, 0, 0], [1, 2, 3, 4, 5]))
得到的图结构如下图所示:

注意边的索引跟创建时候的节点对顺序是一样的。
如果要创建无向图,把上面的节点信息调换并double一倍即可。具体可以使用dgl.add_reverse_edges函数。
# Print the source and destination nodes of every edge.
print(g.edges())
结果:
(tensor([0, 0, 0, 0, 0]), tensor([1, 2, 3, 4, 5]))
点和边的特征表示
DGL中的点和边的特征通常使用同样大小的维度。可以把点和边的特征保存在上面提到的ndata和edata里面,因为这两个玩意是字典,因此可以加入我们自定义的key,例如:
# Assign a 3-dimensional node feature vector for each node.
# 为节点添加3维特征
g.ndata['x'] = torch.randn(6, 3)
# Assign a 4-dimensional edge feature vector for each edge.
# 为边添加4维特征
g.edata['a'] = torch.randn(5, 4)
# Assign a 5x4 node feature matrix for each node. Node and edge features in DGL can be multi-dimensional.
# 为节点添加5*4维的特征
g.ndata['y'] = torch.randn(6, 5, 4)
print(g.edata['a'])
上面打印出来的边特征如下图所示:

一共五行,每行代表一个边
对于不同类型的节点,官方给出了一些特征表示是建议:
For categorical attributes (e.g. gender, occupation), consider converting them to integers or one-hot encoding.独热编码
For variable length string contents (e.g. news article, quote), consider applying a language model.文本
For images, consider applying a vision model such as CNNs.图像
查询图结构信息
print(g.num_nodes())#打印节点数量
print(g.num_edges())#打印边数量
# Out degrees of the center node
print(g.out_degrees(0))#打印节点0的出度
# In degrees of the center node - note that the graph is directed so the in degree should be 0.
print(g.in_degrees(0))#打印节点0的入度
结果:
6
5
5
0
图的切割
这里叫切割,实际上是提取子图的操作。
# Induce a subgraph from node 0, node 1 and node 3 from the original graph.
# 根据节点提取子图
sg1 = g.subgraph([0, 1, 3])
# Induce a subgraph from edge 0, edge 1 and edge 3 from the original graph.
# 根据边获取子图
sg2 = g.edge_subgraph([0, 1, 3])
得到的结果如下:
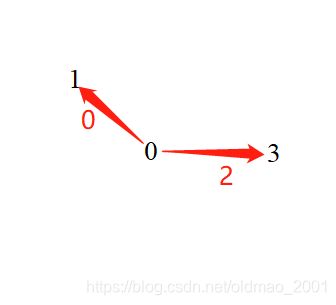

可以把上面提取的两个子图的节点和边信息打印一下:
# The original IDs of each node in sg1
print(sg1.ndata[dgl.NID])
# The original IDs of each edge in sg1
print(sg1.edata[dgl.EID])
# The original IDs of each node in sg2
print(sg2.ndata[dgl.NID])
# The original IDs of each edge in sg2
print(sg2.edata[dgl.EID])
结果:
子图1
tensor([0, 1, 3])
tensor([0, 2])
子图2
tensor([0, 1, 2, 4])
tensor([0, 1, 3])
打印两个子图的特征信息:
# The original node feature of each node in sg1
print(sg1.ndata['x'])
# The original edge feature of each node in sg1
print(sg1.edata['a'])
# The original node feature of each node in sg2
print(sg2.ndata['x'])
# The original edge feature of each node in sg2
print(sg2.edata['a'])
newg = dgl.add_reverse_edges(g)
newg.edges()
结果:
(tensor([0, 0, 0, 0, 0, 1, 2, 3, 4, 5]),
tensor([1, 2, 3, 4, 5, 0, 0, 0, 0, 0]))
保存和加载图
# Save graphs
dgl.save_graphs('graph.dgl', g)
dgl.save_graphs('graphs.dgl', [g, sg1, sg2])
# Load graphs
(g,), _ = dgl.load_graphs('graph.dgl')
print(g)
(g, sg1, sg2), _ = dgl.load_graphs('graphs.dgl')
print(g)
print(sg1)
print(sg2)
消息传递框架Message passing
本节以GraphSAGE为例,进行讲解,整个DGL是参考了MPNN框架中整理的消息传递框架,大多数GNN模型都可以套用整个消息传递框架,GraphSAGE也不例外。
GraphSAGE的套路和节点分类套路一样:先定义自己的卷积层,然后用卷积层堆叠GNN。

这里把原来的MPNN的消息传递公式拆分了一下,第一个公式对应update_all中的message_func,第二个公式对应reduce_func。
加载各种包:
import dgl
import torch
import torch.nn as nn
import torch.nn.functional as F
自定义SAGEConv
虽然DGL有专门的GraphSAGE的卷积方式SAGEConv,但是这里我们自己创建自己的GraphSAGE卷积层。
import dgl.function as fn
class SAGEConv(nn.Module):
"""Graph convolution module used by the GraphSAGE model.
Parameters
----------
in_feat : int
Input feature size.
out_feat : int
Output feature size.
"""
def __init__(self, in_feat, out_feat):
super(SAGEConv, self).__init__()
# A linear submodule for projecting the input and neighbor feature to the output.
# 这里的输入特征*2的原因是下面图中的公式对把当前节点的特征进行了concat
self.linear = nn.Linear(in_feat * 2, out_feat)
def forward(self, g, h):
"""Forward computation
Parameters
----------
g : Graph
The input graph.
h : Tensor
The input node feature.
"""
#local_scope里面的代码不会改变其他全局的信息,类似一个局部变量
#在local_scope中进行特征的操作非常方便,它直接使用原始的特征初始值,但不会修改特征的初始值(除非是in-place操作),具体看https://docs.dgl.ai/generated/dgl.DGLGraph.local_scope.html?highlight=local_scope#dgl.DGLGraph.local_scope
with g.local_scope():
g.ndata['h'] = h# 节点特征放进来
# update_all is a message passing API.
# https://docs.dgl.ai/generated/dgl.DGLGraph.update_all.html?highlight=update_all#dgl.DGLGraph.update_all
# 先把要传递的消息copy出来,当然还有别的消息定义方式,然后进行aggregate操作,这里用的是mean,得到的结果放h_N
g.update_all(message_func=fn.copy_u('h', 'm'), reduce_func=fn.mean('m', 'h_N'))
h_N = g.ndata['h_N']
#将h_N和h按行进行拼接,例如N*5的变成N*10,因此维度也就变成in_feat * 2
h_total = torch.cat([h, h_N], dim=1)
#进入linear层
return self.linear(h_total)
定义GraphSAGE模型
有了单层的SAGEConv卷积,就可以堆叠GraphSAGE模型了
class Model(nn.Module):
def __init__(self, in_feats, h_feats, num_classes):
super(Model, self).__init__()
self.conv1 = SAGEConv(in_feats, h_feats)#第一层
self.conv2 = SAGEConv(h_feats, num_classes)#第二层
#这里的维度参数上面基本操作的例子
def forward(self, g, in_feat):
h = self.conv1(g, in_feat)
h = F.relu(h)
h = self.conv2(g, h)
return h
训练
import dgl.data
# 加载Cora数据集
dataset = dgl.data.CoraGraphDataset()
g = dataset[0]#单图取第0个
def train(g, model):
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
all_logits = []
best_val_acc = 0
best_test_acc = 0
features = g.ndata['feat']
labels = g.ndata['label']
train_mask = g.ndata['train_mask']
val_mask = g.ndata['val_mask']
test_mask = g.ndata['test_mask']
for e in range(200):#200个epoch
# Forward
logits = model(g, features)
# Compute prediction
pred = logits.argmax(1)
# Compute loss
# Note that we should only compute the losses of the nodes in the training set,
# i.e. with train_mask 1.
loss = F.cross_entropy(logits[train_mask], labels[train_mask])
# Compute accuracy on training/validation/test
train_acc = (pred[train_mask] == labels[train_mask]).float().mean()
val_acc = (pred[val_mask] == labels[val_mask]).float().mean()
test_acc = (pred[test_mask] == labels[test_mask]).float().mean()
# Save the best validation accuracy and the corresponding test accuracy.
if best_val_acc < val_acc:
best_val_acc = val_acc
best_test_acc = test_acc
# Backward
optimizer.zero_grad()
loss.backward()
optimizer.step()
all_logits.append(logits.detach())
if e % 5 == 0:
print('In epoch {}, loss: {:.3f}, val acc: {:.3f} (best {:.3f}), test acc: {:.3f} (best {:.3f})'.format(
e, loss, val_acc, best_val_acc, test_acc, best_test_acc))
model = Model(g.ndata['feat'].shape[1], 16, dataset.num_classes)
train(g, model)
GraphSAGE的变形
如果我们考虑节点的权重,那么在进行aggregate取平均的时候就变成加权平均操作,要实现这么一个模型,我们可以按套路,先定义带权GraphSAGE卷积层,然后定义带权GraphSAGE模型。
带权GraphSAGE卷积层
update_all代码有变化,其他代码无变化
class WeightedSAGEConv(nn.Module):
"""Graph convolution module used by the GraphSAGE model with edge weights.
Parameters
----------
in_feat : int
Input feature size.
out_feat : int
Output feature size.
"""
def __init__(self, in_feat, out_feat):
super(WeightedSAGEConv, self).__init__()
# A linear submodule for projecting the input and neighbor feature to the output.
self.linear = nn.Linear(in_feat * 2, out_feat)
def forward(self, g, h, w):
"""Forward computation
Parameters
----------
g : Graph
The input graph.
h : Tensor
The input node feature.
w : Tensor
The edge weight.
"""
with g.local_scope():
g.ndata['h'] = h
g.edata['w'] = w
#可以看到消息中加入了权重,u_mul_e是elementwise的乘法
g.update_all(message_func=fn.u_mul_e('h', 'w', 'm'), reduce_func=fn.mean('m', 'h_N'))
h_N = g.ndata['h_N']
h_total = torch.cat([h, h_N], dim=1)
return self.linear(h_total)
定义模型
代码不变,卷积层换了一下,前向传播函数加了一个权重参数
class Model(nn.Module):
def __init__(self, in_feats, h_feats, num_classes):
super(Model, self).__init__()
self.conv1 = WeightedSAGEConv(in_feats, h_feats)
self.conv2 = WeightedSAGEConv(h_feats, num_classes)
def forward(self, g, in_feat):
# 这里生成的每个边的权重都是1,因此只是演示用而已,并没有起到权重的作用
h = self.conv1(g, in_feat, torch.ones(g.num_edges()).to(g.device))
h = F.relu(h)
h = self.conv2(g, h, torch.ones(g.num_edges()).to(g.device))
return h
训练
这里直接用前面的train函数就可以训练了
model = Model(g.ndata['feat'].shape[1], 16, dataset.num_classes)
train(g, model)
边预测
边预测也是GNN非常重要的任务。通用模型实验部分必做两个任务:节点分类和边预测。
边预测可以用在:social recommendation(社交网络好友推荐), item recommendation(电商根据购买历史进行商品推荐), knowledge graph completion(知识图谱补全)等任务上。
边预测任务可以看做是一个二分类任务;当节点之间存在边,则可以看做是正样本,反之为负样本;使用AUC曲线来衡量模型的好坏;在一些预测模型中的预测结果是top-K的,类似于推荐前K个商品。
我们要训练一个GNN模型来预测模型中的两个节点是否存在边。
预处理
先导入包:
import dgl
import torch
import torch.nn as nn
import torch.nn.functional as F
import itertools
import numpy as np
import scipy.sparse as sp#处理稀疏矩阵的包
导入数据:
import dgl.data
dataset = dgl.data.CoraGraphDataset()
g = dataset[0]
# Split edge set for training and testing
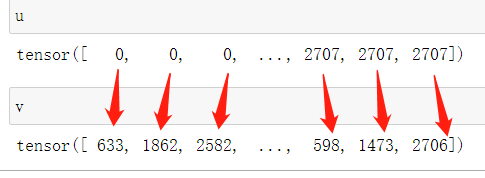
# 从边分出源点和目标点
u, v = g.edges()
eids = np.arange(g.number_of_edges())#根据边的数量生成对应的顺序数字作为id,并放到array里面:
print(eids)
eids = np.random.permutation(eids)#将id进行shuffle打乱
print(eids)
test_size = int(len(eids) * 0.1)#取10%做训练集
print(test_size)
train_size = g.number_of_edges() - test_size#剩下的做测试
print(train_size)
test_pos_u, test_pos_v = u[eids[:test_size]], v[eids[:test_size]]#取训练集中的源点和目标点
print(test_pos_u.shape)
print(test_pos_u)
print(test_pos_v)
train_pos_u, train_pos_v = u[eids[test_size:]], v[eids[test_size:]]#取测试集中的源点和目标点
print(train_pos_u.shape)
print(train_pos_u)
print(train_pos_v)
结果:
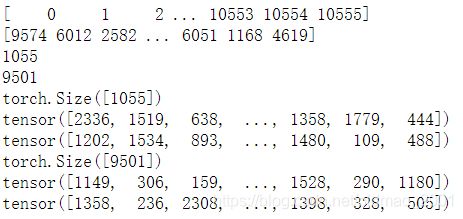
由于有边的节点在图中是不多的,因此整个邻接矩阵是稀疏的,用专门的处理稀疏矩阵的包比较高效,实际只用保存有边的节点在矩阵中的行列坐标即可:
# Find all negative edges and split them for training and testing
adj = sp.coo_matrix((np.ones(len(u)), (u.numpy(), v.numpy())))#邻接矩阵的稀疏存储
adj_neg = 1 - adj.todense() - np.eye(g.number_of_nodes())#邻接矩阵反位(除对角线)
neg_u, neg_v = np.where(adj_neg != 0)#求负样本的源点和目标点
如果要看邻接矩阵可以这样:

上图有1的位置表示有边,0的位置表示么有边。
然后求邻接矩阵的反位,就是0变1,1变0,当然这里对角线上的0保持不变,我们不考虑节点本身是连接关系。
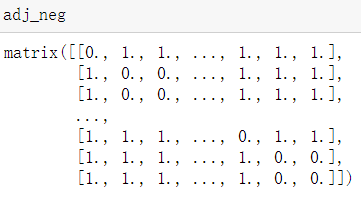
从上面反位的矩阵位置为1的地方都是负样本,找出这些负样本的源点和目标点:

随机采样负样本id,随机采样个数如下所示:
print(len(neg_u))#7320000
print(g.number_of_edges())#10556
neg_eids = np.random.choice(len(neg_u), g.number_of_edges())
想想为什么要随机采样这个数量?因为要和正样本数量匹配,好同步划分测试和训练集。
然后把负样本的源点和目标点取出来:
test_neg_u, test_neg_v = neg_u[neg_eids[:test_size]], neg_v[neg_eids[:test_size]]
train_neg_u, train_neg_v = neg_u[neg_eids[train_size:]], neg_v[neg_eids[train_size:]]
把测试集中的正样本(边)去掉,否则把标准答案给模型训练就没有什么意义了:
train_g = dgl.remove_edges(g, eids[:test_size])
定义GraphSAGE模型
这里的套路和前面意义,不过我们不需要自己定义GraphSAGE卷积层了,用DGL自带的:
from dgl.nn import SAGEConv
# ----------- 2. create model -------------- #
# build a two-layer GraphSAGE model
class GraphSAGE(nn.Module):
def __init__(self, in_feats, h_feats):
super(GraphSAGE, self).__init__()
self.conv1 = SAGEConv(in_feats, h_feats, 'mean')#第一层
self.conv2 = SAGEConv(h_feats, h_feats, 'mean')#第二层
def forward(self, g, in_feat):
h = self.conv1(g, in_feat)
h = F.relu(h)
h = self.conv2(g, h)
return h
要做边的预测,要丢两个点的embedding,然后用一个函数(NN)计算两个点的结果是否有边:
y ^ u ∼ v = f ( h u , h v ) \hat y_{u\sim v}=f(h_u,h_v) y^u∼v=f(hu,hv)
正样本图+负样本图
由上面的公式我们可以看到在边预测的时候需要一对节点的embedding,DGL推荐以下操作来进行操作:保持所有节点不变,将所有正样本边放一个图(正样本图),所有负样本边放一个图(负样本图),如果再按训练集和测试集进行划分,总共就四张图。
train_pos_g = dgl.graph((train_pos_u, train_pos_v), num_nodes=g.number_of_nodes())
train_neg_g = dgl.graph((train_neg_u, train_neg_v), num_nodes=g.number_of_nodes())
test_pos_g = dgl.graph((test_pos_u, test_pos_v), num_nodes=g.number_of_nodes())
test_neg_g = dgl.graph((test_neg_u, test_neg_v), num_nodes=g.number_of_nodes())
这样划分的好处就是可以用DGL的DGLGraph.apply_edges方法来计算两个节点的embedding是否会有边。
import dgl.function as fn
class DotPredictor(nn.Module):
def forward(self, g, h):
with g.local_scope():
g.ndata['h'] = h
# Compute a new edge feature named 'score' by a dot-product between the
# source node feature 'h' and destination node feature 'h'.
# u_dot_v相当于上面公式里面的f,当然也可以使用自己定义的NN,这里是计算当前节点和其他所有节点的点乘
g.apply_edges(fn.u_dot_v('h', 'h', 'score'))
# u_dot_v returns a 1-element vector for each edge so you need to squeeze it.
return g.edata['score'][:, 0]#去掉上面点乘出来的多余维度
点乘计算也可以换成自定义的NN,例如:
class MLPPredictor(nn.Module):
def __init__(self, h_feats):
super().__init__()
self.W1 = nn.Linear(h_feats * 2, h_feats)
self.W2 = nn.Linear(h_feats, 1)
def apply_edges(self, edges):
"""
Computes a scalar score for each edge of the given graph.
Parameters
----------
edges :
Has three members ``src``, ``dst`` and ``data``, each of
which is a dictionary representing the features of the
source nodes, the destination nodes, and the edges
themselves.
Returns
-------
dict
A dictionary of new edge features.
"""
h = torch.cat([edges.src['h'], edges.dst['h']], 1)
return {'score': self.W2(F.relu(self.W1(h))).squeeze(1)}#将多余维度去掉
def forward(self, g, h):
with g.local_scope():
g.ndata['h'] = h
g.apply_edges(self.apply_edges)
return g.edata['score']
训练
model = GraphSAGE(train_g.ndata['feat'].shape[1], 16)#初始化模型
# You can replace DotPredictor with MLPPredictor.
#pred = MLPPredictor(16)
pred = DotPredictor()#选择简单的点乘方式计算
损失函数用的binary cross entropy
L = − ∑ u ∼ v ∈ D ( y u ∼ v log ( y ^ u ∼ v ) + ( 1 − y u ∼ v ) log ( 1 − y ^ u ∼ v ) ) ) \mathcal{L} = -\sum_{u\sim v\in \mathcal{D}}\left( y_{u\sim v}\log(\hat{y}_{u\sim v}) + (1-y_{u\sim v})\log(1-\hat{y}_{u\sim v})) \right) L=−u∼v∈D∑(yu∼vlog(y^u∼v)+(1−yu∼v)log(1−y^u∼v)))
def compute_loss(pos_score, neg_score):
scores = torch.cat([pos_score, neg_score])#分别算正样本和负样本score
labels = torch.cat([torch.ones(pos_score.shape[0]), torch.zeros(neg_score.shape[0])])#根据pos_score,neg_score的形状设置ground truth标签
return F.binary_cross_entropy_with_logits(scores, labels)#用预测值和标签
def compute_auc(pos_score, neg_score):
scores = torch.cat([pos_score, neg_score]).numpy()
labels = torch.cat(
[torch.ones(pos_score.shape[0]), torch.zeros(neg_score.shape[0])]).numpy()
return roc_auc_score(labels, scores)
设置优化器
optimizer = torch.optim.Adam(itertools.chain(model.parameters(), pred.parameters()), lr=0.01)
训练
all_logits = []
for e in range(100):
# forward
h = model(train_g, train_g.ndata['feat'])
pos_score = pred(train_pos_g, h)
neg_score = pred(train_neg_g, h)
loss = compute_loss(pos_score, neg_score)
# backward
optimizer.zero_grad()
loss.backward()
optimizer.step()
if e % 5 == 0:
print('In epoch {}, loss: {}'.format(e, loss))
# ----------- 5. check results ------------------------ #
from sklearn.metrics import roc_auc_score
with torch.no_grad():
pos_score = pred(test_pos_g, h)
neg_score = pred(test_neg_g, h)
print('AUC', compute_auc(pos_score, neg_score))