GPS卫星位置计算（卫星位置计算小程序）java版

目录

 

一、准备以及结果图

二、数据

三、计算

四、全部代码

附：

---

 

 

一、准备以及结果图

软件：eclipse（2020-6版本）带有WindowBuilder插件

编程语言：Java

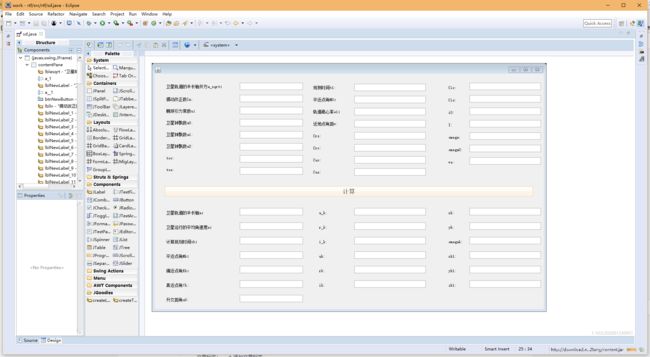
结果图：

 

二、数据

t0e	星历的基准时间单位：秒
a_sqrt	轨道半长轴的平方根单位：米
e1	轨道离心率单位：无量纲
i0	倾角（在 t0e时）单位：rad 弧度
omega0	升交点经度（在每星期历元上）单位：rad 弧度
M0	平均近点角（在 t0e时）单位：rad 弧度
I	倾角的变化率单位：rad/s弧度/秒
omega	升交点经度的变化率单位：rad/s弧度/秒
ln	对平均角速度的校正值单位：rad/s弧度/秒
Cuc	对纬度幅角余弦的校正值单位：rad 弧度
Cus	对纬度幅角正弦的校正值单位：rad 弧度
Crc	对轨道半径余弦的校正值单位：米
Crs	对轨道半径正弦的校正值单位：米
Cic	对倾角余弦的校正值单位：rad 弧度
Cis	对倾角正弦的校正值单位：rad 弧度

 

• 椭球引力常数:  μ = 3.986005e14 m3s-2(GPS )
• 地球自转角速度 we = 7.2921151467e-5 （rad/s）
• t1=4800.0;            // 观测时间
• toe=0.00000000000000000;    // 星历基准时间
• toc=0.00000000000000000;    // 卫星钟基准时间
• a_sqrt =  5153.7127704599998 //轨道半长轴平方根
• //卫星钟飘参数
• a0 =  0.00028600683435800001
• a1 =  1.7053025658199999e-012
• a2 =  0
• //平均角速度摄动改正参数
• ln =  4.1115998360700002e-009
• //参考时刻的平近点角
• M0     =  1.2263973009600000
• //轨道离心率
• e1     =  0.0053100715158500003
• //近地点角距
• w    =  -1.6819446292500000
• //对轨道半径正弦的修正值
• Crs   =  -105.43750000000000
• //在轨道径向方向上周期改正余余弦的振幅
• Crc   =  175.34375000000000
• //轨道延迹方向上周期改正余弦振幅
• Cuc   =  -5.5264681577700003e-006
• //轨道延迹方向上周期改正正弦振幅
• Cus   =  1.1192634701700000e-005
• //轨道倾角周期改正余弦项振幅
• Cic   =  -9.6857547759999998e-008
• //轨道倾角周期改正正弦项振幅
• Cis   =  -7.8231096267699997e-008
• //参考时刻升交点赤径主项
• omega0   =  -2.9080127721900002
• //升交点赤径在赤道平面中的长期变化
• omega     =  -7.7124641122299999e-009
• //参考时间轨道倾角
• i0    =  0.97432927738800001
• //轨道倾角变化率
• I    =  1.8643633724999999e-010

 

三、计算

计算卫星轨道半长轴

double a_sqrt = Double.parseDouble(a_1.getText().trim());
double a = a_sqrt * a_sqrt;
String Sa = "" + a;
a__1.setText(Sa);

计算卫星运动的平均角速度n

double ln = Double.parseDouble(ln_2.getText().trim());
double u = Double.parseDouble(u_2.getText().trim());
double n0 = Math.pow(u / Math.pow(a, 3), 0.5);
double n = n0 + ln;
String Sn = "" + n;
n_2.setText(Sn);

计算规划时间

double toe = Double.parseDouble(toe_1.getText().trim());
double toc = Double.parseDouble(toc_1.getText().trim());
double t1 = Double.parseDouble(t1_1.getText().trim());
double a0 = Double.parseDouble(a0_1.getText().trim());
double a1 = Double.parseDouble(a1_1.getText().trim());
double a2 = Double.parseDouble(a2_1.getText().trim());
double lt = a0 + a1 * (t1 - toc) + a2 * ((t1 - toc) * (t1 - toc));// 计算卫星钟差
double t = t1 - lt;
double tk = t - toe;
String Stk = "" + tk;
tk_1.setText(Stk);

计算真近点角Vk

double M0 = Double.parseDouble(M0_1.getText().trim());
double e1 = Double.parseDouble(e_1.getText().trim());
double Mk = M0 + n * tk;
String SMk = "" + Mk;
Mk_1.setText(SMk);

double Ek_old = Mk;
double Ek_new = Mk + e1 * Math.sin(Ek_old);
int i = 1;
while (Math.abs(Ek_new - Ek_old) > 10e-8) {
	Ek_old = Ek_new;
	Ek_new = Mk + e1 * Math.sin(Ek_old);
	i += 1;
	if (i > 10)// ?
		break;
	}
	double Ek = Ek_new;
	String SEk = "" + Ek;
	Ek_1.setText(SEk);

double Vk1 = (Math.pow(1 - e1 * e1, 0.5) * Math.sin(Ek)) / (1 - e1 * Math.cos(Ek));// sinVk
double Vk2 = (Math.cos(Ek) - e1) / (1 - e1 * Math.cos(Ek)); // cosVk
double Vk;
	if (Vk2 == 0) {
		if (Vk1 > e1)
			Vk = Math.PI / 2;
		else
			Vk = -Math.PI / 2;
	} else {
		Vk = Math.atan(Vk1 / Vk2);
		if (Vk2 < 0) {
			if (Vk1 >= 0)
				Vk += Math.PI;
			else
				Vk -= Math.PI;
		}
	}
String SVk = "" + Vk;
Vk_1.setText(SVk);

计算升交距角u0

double w = Double.parseDouble(w_1.getText().trim());
double u0 = Vk + w;
String Su0 = "" + u0;
u0_1.setText(Su0);

计算经过摄动改正的升交距角uk、卫星的地心距离rk、轨道倾角ik

double Crs = Double.parseDouble(Crs_1.getText().trim());
double Crc = Double.parseDouble(Crc_1.getText().trim());
double Cuc = Double.parseDouble(Cuc_1.getText().trim());
double Cus = Double.parseDouble(Cus_1.getText().trim());
double Cic = Double.parseDouble(Cic_1.getText().trim());
double Cis = Double.parseDouble(Cis_1.getText().trim());
double i0 = Double.parseDouble(i0_1.getText().trim());
double I = Double.parseDouble(I_1.getText().trim());
double u_k = Cus * Math.sin(2 * u0) + Cuc * Math.cos(2 * u0);
double r_k = Crs * Math.sin(2 * u0) + Crc * Math.cos(2 * u0);
double i_k = Cis * Math.sin(2 * u0) + Cic * Math.cos(2 * u0);

String Su_k = "" + u_k;
u_k_1.setText(Su_k);
String Sr_k = "" + r_k;
r_k_1.setText(Sr_k);
String Si_k = "" + i_k;
i_k_1.setText(Si_k);

double uk = u0 + u_k;
double rk = a * (1 - e1 * Math.cos(Ek)) + r_k;
double ik = i0 + i_k + I * tk;

String Suk = "" + uk;
uk_1.setText(Suk);
String Srk = "" + rk;
rk_1.setText(Srk);
String Sik = "" + ik;
ik_1.setText(Sik);

计算卫星的轨道平面直角坐标

double xk = rk * Math.cos(uk);
double yk = rk * Math.sin(uk);

String Sxk = "" + xk;
xk_1.setText(Sxk);
String Syk = "" + yk;
yk_1.setText(Syk);

坐标转换

double omega = Double.parseDouble(omega_1.getText().trim());
double omega0 = Double.parseDouble(omega0_1.getText().trim());
double we = Double.parseDouble(we_1.getText().trim());
double omegak = omega0 + omega * (t - toe) - we * t;
String Somegak = "" + omegak;
omegak_1.setText(Somegak);

double xk1 = xk * Math.cos(omegak) - yk * Math.cos(ik) * Math.sin(omegak);
double yk1 = xk * Math.sin(omegak) + yk * Math.cos(ik) * Math.cos(omegak);
double zk1 = yk * Math.sin(ik);

String Sxk1 = "" + xk1;
xk1_1.setText(Sxk1);
String Syk1 = "" + yk1;
yk1_1.setText(Syk1);
String Szk1 = "" + zk1;
zk1_1.setText(Szk1);

四、全部代码见另一篇

附：

结果图数据：

a_sqrt:5153.7127704599998

ln:4.1115998360700002e-009

u:3.986005e14

a0:0.00028600683435800001

a1:1.7053025658199999e-012

a2:0

toc:0

toe:0

t1:4800

M0:1.2263973009600000

e1:0.0053100715158500003

w:-1.6819446292500000

Crs:-105.43750000000000

Crc:175.34375000000000

Cuc:-5.5264681577700003e-006

Cus:1.1192634701700000e-005

Cic:-9.6857547759999998e-008

Cis:-7.8231096267699997e-008

i0:0.97432927738800001

I:1.8643633724999999e-010

omega:-7.7124641122299999e-009

omega0:-2.9080127721900002

we:7.2921151467e-5

 

代入数据结果图：

 

 

a=a_sqrt*a_sqrt	半轴长
n=ln+(u/a^3)^1/2	经校正的平均角速度
lt= a0+a1(t-toc)+a2(t-toc)^2	计算卫星种差
tk = t - toe	从星历历元算起的时间
Mk = M0 + n * tk	平均近点角
Ek= Mk + e1 * sin(Ek)	k为偏心近点角，必须用迭代法解出
sinVk=(Math.pow(1 - e1 * e1, 0.5) * sin(Ek)) / (1 - e1 * cos(Ek)) cosVk=(cos(Ek) - e1) / (1 - e1 * cos(Ek))	真近点角
u0 = Vk + w	升交距角
u_k = Cus * sin(2 * u0) + Cuc * cos(2 * u0)	升交距角校正值
r_k = Crs * Math.sin(2 * u0) + Crc * Math.cos(2 * u0)	向径校正值
i_k = Cis * Math.sin(2 * u0) + Cic * Math.cos(2 * u0)	倾角校正值
uk = u0 + u_k	经校正的升交距角
rk = a * (1 - e1 * Math.cos(Ek)) + r_k	经校正的向径
ik = i0 + i_k + I * tk	经校正的倾角
omegak = omega0 + omega * (t - toe) - we * t	经校正的升交点经度 地球自转角速度
xk = rk * Math.cos(uk)	在轨道平面中的x位置
yk = rk * Math.sin(uk)	在轨道平面中的y位置
xk1 = xk * Math.cos(omegak) - yk * Math.cos(ik) * Math.sin(omegak)	ECEF x坐标
yk1 = xk * Math.sin(omegak) + yk * Math.cos(ik) * Math.cos(omegak)	ECEF y坐标
zk1 = yk * Math.sin(ik)	ECEF z坐标