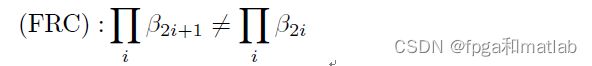【GF(q)+LDPC】基于二值图GF(q)域的规则LDPC编译码设计与matlab仿真
1.软件版本
matlab2017b
2.系统原理
首先假设环长l,如果二进制矩阵的秩是满秩,那么这个环没有包含于二进制最小距离中,假设g=lmin为校验矩阵的环长。那么每一个二进制矩阵(其环长在lmin和lmax)之间,那么就可以降低误码率,提高性能。这里论文中给出的满秩条件FRC的描述如下所示:
给出一个方块矩阵Cd,其环长为d=l/2;通过行列变换,可以得到如下的式子:
那么其满秩条件为det(Cd)不等于0。这个等效于如下的条件:
所以,我们在进行消环的时候,我们将通过循环的方法,通过不断的进行行列变换,满足上述条件,从而得到消环效果。
再介绍停止集:
系统的性能,除了和环相关,还和停止集相关,在实际中,没有具体的方法去消除停止集所带来的影响,通常的做法是:
假设ds是一个给定的停止集的权值,那么对应的规则图形(矩阵)其最小的停止集的权值为dsmin=3g/4.,这里g为环长。在实际中,为了提供系统的性能,需要最大化停止集的最小距离。
然后使用论文最后给出的四个步骤进行循环优化。
整个二进制图像算法的大概步骤为:
第一步:初始化,初始化的步骤就是从初始的H校验矩阵中随机的选择几行,这些行主要来及行集合R以及他们的排列组合中。通过步骤一,我们将得到不同排列组合的几个R的行数据构造的矩阵H。
第二步:这个步骤的主要目的就是删除环长在g和LM之间的环。包括集合S中的停止集,从而获得较好性能的环和停止集状态。设置矩阵H的一组行的标号集合I,然后开始迭代计算,直接矩阵的最大环长大于LM。即消除了整个矩阵中的小环。
具体步骤为:
2.1:初始化随机选择I,这里I 是H矩阵中的所有的行标号的集合的子集合或者全集,这里我们选择所有的行标号作为被优化目标。
2.2:从I中随机的选择一个行标号。
2.3:从矩阵R中随机一个n个随机排列的集合 ![]()
2.4:选择![]() 一个组合,保证一些小的环长的环尽可能的被删除,对于每个循环下的l,搜索比l小的围长,然后删除。
一个组合,保证一些小的环长的环尽可能的被删除,对于每个循环下的l,搜索比l小的围长,然后删除。
2.5:将集合I中去除本次循环所被删除的环的所在行的标号,然后再循环,直接I变为空集合。
第三步:消环和停止集处理:
这个步骤,主要是针对一些围长大于LM的情况,进行删除,以及对S中的停止集的选择满足最小距离的最大化处理。
第四步:如果没有可以消除的环或者没有S中的停止集的选择满足最小距离的最大化处理发生改变的情况,那么完成这四个步骤的优化过程,否则继续开始上面四个步骤的循环。
关于2,4性能较好的分析
这个只能从相对的角度来分析,因为行重为2的时候,如果系统中存在一个4环,那么这个矩形的两个点分别是对应的行重的两个非0元素,另外两个点是另外一列重的两个非零元素,当列重为4的时候,出现4环的概率要小于2,6,28,210出现四环的概率,
当然,既然能构造出H矩阵,那么一般都是没有四环的,这个时候,就需要考虑六环的结构,六环存在如下几种情况:
同样道理,在列上出现当列重为4的时候,其出现六环的概率远小于列重大于4的情况。如果都没有六环,那么考虑八环的情况。一次类推。
但是2,4的性能又会比2,3性能差些。
从仿真角度考虑,你可以产生不同行重,列重的矩阵,进行仿真对比一下。上面的是从理论角度进行分析的。
3.核心源码
function H = func_good_Hgf32(H0,N);
H = zeros(size(H0));
H = func_randomly(H0,N);
H0 = H;
%%
%Initialization
%The rows values in H are chosen at random from the rows in R and their random permutations
%产生random permutations构成的H矩阵
R = H0;
%随机排列组合
[M,N] = size(H0);
indcol= randperm(M);%行的随机排列
indrow= randperm(N);%列的随机排列
%行排列
for i = 1:M
H(i,:) = R(indcol(i),:);
end
for i = 1:N
H(:,i) = R(:,indrow(i));
end
%产生不同排列组合的R
NUM = N;%设置一个集合
for j = 1:NUM
indcol= randperm(M);%行的随机排列
indrow= randperm(N);%列的随机排列
%行排列
for i = 1:M
Hj(i,:) = R(indcol(i),:);
end
for i = 1:N
Hj(:,i) = R(:,indrow(i));
end
RR{j} = Hj;
end
%%
%Initial cycle cancellation:
ROW_SET = [1:M];
I = ROW_SET;
n = floor(M/2);
g = 1;
LM = 6;
l = g;
MM = length(I);
while(MM > 0)%当为1的时候,则为1,停止循环
for l = g:1:LM
%2.2:从I中随机的选择一个行标号。
tmps = randperm(M);
Index = tmps(1);
%2.3:从R中随机选择n个组合;
for i = 1:n
R_tmps{i} = RR{Index+i-1};
end
%2.4:最大化围长值,然后删除这个集合
for i = 1:n
R_tmps{i} = RR{Index+i-1};
if rank(R_tmps{i}) == M
R_tmps{i} = [];
RR{Index+i-1} = zeros(size(RR{Index+i-1}));
end
end
end
%2.5:本次循环结束,去掉随机的Index
MM = MM-1;
end
%去除被排除的组合方法
Index2 = 0;
for i = 1:NUM
if sum(RR{i}) > 0;
Index2 = Index2 + 1;
RR2{Index2} = RR{i};
end
end
%%
%Cycle cancellation and stopping set mitigation
%先进行消环
Index3 = 0;
RR3 = RR2;
for i = 1:Index2
%检测是否存在大于LM的环长,如果存在,则删除,否则不删除
cycle4num = check4cycle(RR3{i});
cycle6num = check6cycle(RR3{i});
cycle8num = check8cycle(RR3{i});
if cycle4num == 0 & cycle6num == 0 & cycle8num == 0
Index3 = Index3 + 1;
RR3{Index3} = RR2{Index3};
elseif cycle4num == 0 & cycle6num == 0 & cycle8num > 0
RR3{Index3} = zeros(size(RR2{Index3}));
end
end
%去除被排除的组合方法
Index4 = 0;
for i = 1:Index3
if sum(RR3{i}) > 0;
Index4 = Index4 + 1;
RR4{Index4} = RR3{i};
end
end
%在剩下的集合中,任意选择一个。
SEL = randperm(Index4);
H = RR4{SEL(1)};
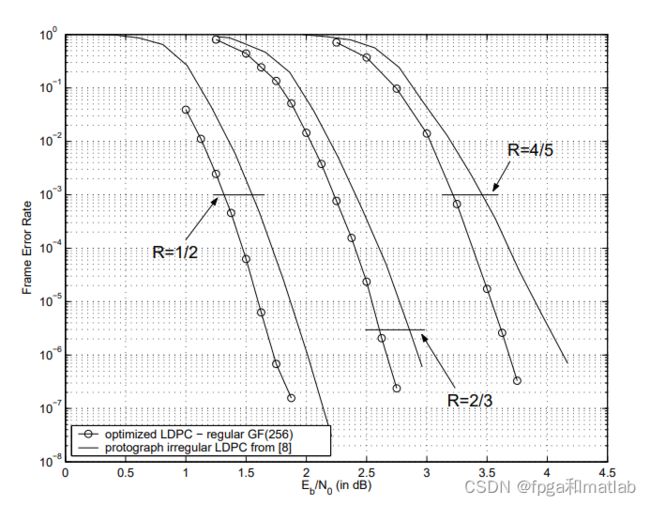
4.测试结果
5.参考文献
[1] Poulliat C , Fossorier M , Declercq D . Design of regular (2,dc)-LDPC codes over GF(q) using their binary images[J]. IEEE Transactions on Communications, 2008, 56(10):1626-1635.A14-14(error)