如何解释模型预测?常用4种可解释性分析方法~
模型可解释性
- 1.为什么要模型可解释性
-
- 2.模型可解释性的应用场景
- 3.模型可解释性理论方法
-
- 3.1 可解释的模型方法
-
- 3.1.1 线性回归
- 3.1.2 树模型
- 3.2 模型无关的方法
-
- 3.2.1 LIME(局部解释)
- 3.2.2 SHAP(全局解释 + 局部解释)
- 4.模型可解释性工具比较
- 5.模型可解释性与模型工作流的集成
-
- 5.1 基于线性回归的特征权重系数
- 5.2 基于树模型(LightGBM)的特征重要性
- 5.3 基于SHAP的可解释性
-
- 5.3.1 全局解释
- 5.3.2 局部解释
- 5.4 基于LIME的可解释性
-
- 5.4.1 局部解释
1.为什么要模型可解释性
- 模型的决策对场景影响越大,模型对它行为的解释就越重要
- 可解释性便于人类理解模型的决策,模型必须“说服” 我们,这样它们才能达到预期的⽬标
- 我们需要模型可解释性来找出问题的隐患,如员工离职预测,我们需要通过可解释性来找出离职背后的真正原因,以采取相应的措施
2.模型可解释性的应用场景
-
Tabular:回归(价格/销量/流量预测) + 分类(违约/ctr/异常检测)
-
NLP:情感分类
-
CV:目标检测 + 识别
3.模型可解释性理论方法
3.1 可解释的模型方法
3.1.1 线性回归
线性回归 (Linear Regression) 模型将⽬标预测为特征输⼊的加权和,⽽所学习关系的线性使解释变得容易。线性模型可⽤于建模回归⽬标 y 对某些特征 x 的依赖性。由于学到的关系是线性的,可以针对第 i个实例写成如下:
y = ∑ i = 1 n w i x i + b y = \sum_{i = 1}^{n} w_ix_i + b y=i=1∑nwixi+b
实例的预测结果是其n 个特征的加权和。参数 w表⽰要学习的特征权重或系数,其中 b称为截距,不与特征相乘。
3.1.2 树模型
基于树的模型根据特征中的某些截断值多次分割 (Split,或称分裂、拆分) 数据。通过分割,可以创建数据集的不同⼦集,每个实例都属于⼀个⼦集。最后的⼦集称为终端 (Terminal) 或叶节点 (Leaf Nodes),中间的⼦集称为内部节点 (Internal Nodes) 或分裂节点 (Split Nodes)。为了预测每个叶节点的结果,使⽤该节点中训练数据的平均结果。树模型可⽤于分类和回归。
 在决策树中,⼀个特征的总体重要性可以⽤以下⽅法计算:遍历使⽤该特征的所有分割,并测量它相对于⽗节点减少了多少⽅差或基尼指数。所有重要性的总和被缩放为 100,这意味着每个重要性可以解释为总体模型重要性的⼀部分。
在决策树中,⼀个特征的总体重要性可以⽤以下⽅法计算:遍历使⽤该特征的所有分割,并测量它相对于⽗节点减少了多少⽅差或基尼指数。所有重要性的总和被缩放为 100,这意味着每个重要性可以解释为总体模型重要性的⼀部分。
3.2 模型无关的方法
3.2.1 LIME(局部解释)
对于一个分类器(复杂模型),想用一个可解释的模型(简单模型如线性规划,搭配可解释的特征进行适配,并且这个可解释模型再局部的表现上很接近复杂模型的效果
![]()
如图所示,红色和蓝色区域表示一个复杂的分类模型(黑盒),图中加粗的红色十字表示需要解释的样本,显然,我们很难从全局用一个可解释的模型(例如线性模型)去逼近拟合它。但是,当我们把关注点从全局放到局部时,可以看到在某些局部是可以用线性模型去拟合的。具体来说,我们从加粗的红色十字样本周围采样,所谓采样就是对原始样本的特征做一些扰动,将采样出的样本用分类模型分类并得到结果(红十字和蓝色点),同时根据采样样本与加粗红十字的距离赋予权重(权重以标志的大小表示)。虚线表示通过这些采样样本学到的局部可解释模型,在这个例子中就是一个简单的线性分类器。在此基础上,我们就可以依据这个局部的可解释模型对这个分类结果进行解释了。
LIME函数分为三个模块进行:
- 目标函数:
解释模型定义为模型g∈G,我们进一步使用πx(z)作为实例z与x之间的接近度,以定义x周围的局部性。定义一个目标函数ξ,这里的L函数作为一个度量,描述如何通过πx在局部定义中,不忠诚的g如何逼近f(复杂模型),在当Ω(g)(解释模型复杂度)足够低可以被人类理解时,我们最小化L函数得到目标函数的最优解。LIME产生的解释如下:
ξ ( x ) = argmin g ∈ G L ( f , g , π x ) + Ω ( g ) \xi(x)=\underset{g \in G}{\operatorname{argmin}} L\left(f, g, \pi_{x}\right)+\Omega(g) ξ(x)=g∈GargminL(f,g,πx)+Ω(g)
- 引入相似度后的目标函数:
对这个样本进行可解释的扰动(即采样),论文中还对扰动前后的样本相似度的距离进行了定义,这取决于样本的类型(文本的话就是余弦相似性,图像的话就是L2范数距离)。则相似度计算公式如下:
π x ( z ) = exp ( − D ( x , z ) 2 σ 2 ) \pi_{x}(z)=\exp \left(-\frac{D(x, z)^{2}}{\sigma^{2}}\right) πx(z)=exp(−σ2D(x,z)2)
- 最终函数
有了相似度的定义,便可以将原先的目标函数改写成如下的形式。其中f(z)就是扰动样本,在d维空间(原始特征)上的预测值,并把该预测值作为答案,g(z’)则是在d’维空间(可解释特征)上的预测值,然后以相似度作为权重,因此上述的目标函数便可以通过线性回归的方式进行优化。
ξ ( x ) = ∑ z ′ , z ∈ Z π x ( z ) ( f ( z ) − g ( z ′ ) ) 2 \xi(x)=\sum_{z^{\prime}, z \in Z} \pi_{x}(z)\left(f(z)-g\left(z^{\prime}\right)\right)^{2} ξ(x)=z′,z∈Z∑πx(z)(f(z)−g(z′))2
通过优化后的目标函数,我们利用岭回归取得对这个样本有影响力的系数,即可表达该特征的LIME值
3.2.2 SHAP(全局解释 + 局部解释)
SHAP 属于模型事后解释的方法,它的核心思想是计算特征对模型输出的边际贡献,再从全局和局部两个层面对“黑盒模型”进行解释。SHAP构建一个加性的解释模型,所有的特征都视为“贡献者”。
对于每个预测样本,模型都产生一个预测值,SHAP value就是该样本中每个特征所分配到的数值
基本思想:计算一个特征加入到模型时的边际贡献,然后考虑到该特征在所有的特征序列的情况下不同的边际贡献,取均值,即某该特征的SHAP baseline value
举个例子,我们可以想象一个机器学习模型(假设是线性回归,但也可以是其他任何机器学习算法),知道这个人的年龄、性别和工作,它可以预测一个人的收入。
Shapley值是基于这样一种想法,即应该考虑每个特征可能的组合的结果来决定单个特征的重要性。在我们的例子中,这对应于f特征的每个可能组合(f从0到F, F是所有可用特征的数量)。
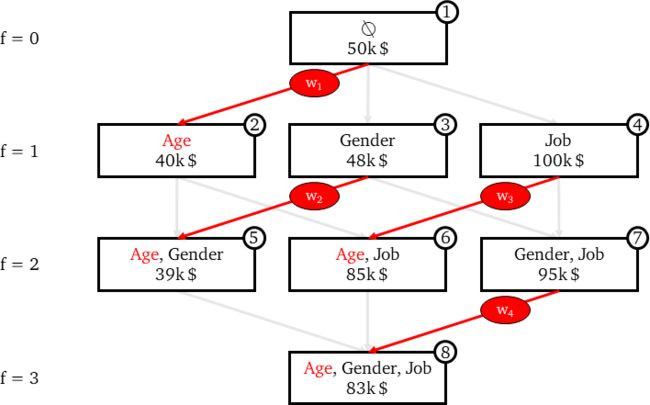
在数学中,这被称为“power set”,可以用树表示。

特征的Power set
每个节点代表一个特征组合,每条边代表包含一个在前一个组合中不存在的特征。
我们从数学上知道一个幂集的容量是2n,其中n是原始集合的元素个数。实际上,在我们的例子中,我们有2^F = 2^3= 8个可能的特征的组合。
现在,SHAP需要为幂集中的每个不同的组合训练一个不同的预测模型,这意味着有2^F个模型。当然,这些模型在涉及到它们的超参数和训练数据时是完全等价的。唯一改变的是模型中包含的一组特征。
假设我们已经在相同的训练数据上训练了8个线性回归模型。我们可以用一个新的观察样本(我们称之为x₀),看看同样的8种不同的模型对这个观察样本的预测。

用不同模型预测x₀。在每个节点上,第一行表示特征的组合,第二行为x₀的模型预测收入。
这里,每个节点代表一个模型。但是边代表什么呢?
正如上面所看到的,由一条边连接的两个节点只因为一个特征而不同,即底部的节点与上部的节点具有完全相同的特征,而上部的节点则没有。因此,两个连接节点的预测之间的差距可以归结为该附加特征的影响。这被称为特性的**“边际贡献”**。
因此,每条边代表一个特征对模型的边际贡献。假设我们在节点1中,节点1是一个没有任何特征的模型。该模型将简单地预测所有训练观察样本值的平均收入(50k美元)。如果我们到了节点2,这是一个模型只有一个特征(年龄),现在对x₀的预测为40k美元。这意味着知道x₀的年龄降低了我们的预测10k美元。
因此,年龄对只包含年龄作为特征的模型的边际贡献是-10k$。公式:
M C Age , { Age } ( x 0 ) = Predict { Age ( x 0 ) − Predict ∅ ( x 0 ) = 40 k $ − 50 k $ = − 10 k $ M C_{\text {Age },\{\text { Age }\}}\left(x_{0}\right)=\operatorname{Predict}_{\{\text {Age }}\left(x_{0}\right)-\operatorname{Predict}_{\varnothing}\left(x_{0}\right)=40 k \$-50 k \$=-10 k \$ MCAge ,{ Age }(x0)=Predict{Age (x0)−Predict∅(x0)=40k$−50k$=−10k$
当然,获得年龄对最终模型的整体效果(即x₀的年龄的SHAP值),有必要考虑年龄在所有出现过模型的边际贡献。在我们的树表示中,这意味着要考虑连接两个节点的所有边:
上一个节点不包含年龄,且
下一个节点中包含年龄
年龄的边际贡献
所有这些边际贡献然后通过加权平均数加以汇总。公式:
SHAP Age ( x 0 ) = w 1 × M C A g e , { A g e } ( x 0 ) + w 2 × M C A g e , { Age,Gender } ( x 0 ) + w 3 × M C A g e , { Age, Job } ( x 0 ) + w 4 × M C A g e , { Age, Gender,Job } ( x 0 ) \begin{aligned} \operatorname{SHAP}_{\text {Age }}\left(x_{0}\right)=& w_{1} \times M C_{A g e,\{A g e\}}\left(x_{0}\right)+\\ & w_{2} \times M C_{A g e,\{\text { Age,Gender }\}}\left(x_{0}\right)+\\ & w_{3} \times M C_{A g e,\{\text { Age, Job }\}}\left(x_{0}\right)+\\ & w_{4} \times M C_{A g e,\{\text { Age, Gender,Job }\}}\left(x_{0}\right) \end{aligned} SHAPAge (x0)=w1×MCAge,{Age}(x0)+w2×MCAge,{ Age,Gender }(x0)+w3×MCAge,{ Age, Job }(x0)+w4×MCAge,{ Age, Gender,Job }(x0)
其中
w 1 + w 2 + w 3 + w 4 = 1 w_1+w_2+w_3+w_4=1 w1+w2+w3+w4=1
我们如何确定边的权重(即4个模型中年龄的边际贡献)?
想法是:
所有边际贡献对具有1个特征的模型的权重之和应等于所有边际贡献对具有2个特征的模型的权重之和,以此类推……,换句话说,同一“行”上所有权值的和应该等于任意其他“行”上所有权值的和。在我们的例子中,这意味着:
w 1 = w 2 + w 3 = w 4 w_1= w_2+ w_3= w_4 w1=w2+w3=w4
对每个f,f个特征的模型的所有的边际贡献的权重应该是相等的。换句话说,同一“行”上的所有边应该相等。在我们的例子中,这意味着:
w 2 = w 3 w_2 = w_3 w2=w3
因此,(记住它们的和应该是1):
w 1 = 1 / 3 w 2 = 1 / 6 w 3 = 1 / 6 w 4 = 1 / 3 w_1 = 1/3\\ w_2 = 1/6\\ w_3 = 1/6\\ w_4 = 1/3\\ w1=1/3w2=1/6w3=1/6w4=1/3
通过上图,我们可以得出一般框架中确定权重的模式:
边的权值是同一“行”中边总数的倒数。或者,同样地,f个特征的模型的边际贡献的权重是可能的边际贡献的数量的倒数。即有最终计算x₀的Age的SHAP值所需的所有元素:
S H A P A g e ( x 0 ) = 1 3 × ( − 10 k $ ) + 1 6 × ( − 9 k $ ) + 1 6 × ( − 15 k $ ) + 1 3 × ( − 12 k $ ) = − 11.33 k SHAP_{Age}(x_0) = \frac{1}{3} \times(-10 k \$)+\frac{1}{6} \times(-9 k \$)+\frac{1}{6} \times(-15 k \$)+\frac{1}{3} \times(-12 k \$)=-11.33 k SHAPAge(x0)=31×(−10k$)+61×(−9k$)+61×(−15k$)+31×(−12k$)=−11.33k
4.模型可解释性工具比较
| —— | 速度 | 处理非线性 | 单一模型限制 | 局部解释 |
|---|---|---|---|---|
| 线性模型 | 快 | 弱 | 限制 | 可局部解释 |
| 树模型 | 快 | 强 | 限制 | 无法局部解释 |
| LIME | 快 | 强 | 限制 | 可局部解释 |
| SHAP | 快 | 强 | 限制 | 可局部解释 |
5.模型可解释性与模型工作流的集成
下面以波士顿房价作为各可解释性方法的Coding演示:
5.1 基于线性回归的特征权重系数
import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# 导入数据
data = pd.DataFrame(load_boston()['data'],columns = load_boston()['feature_names'].tolist())
data['Price'] = load_boston()['target']
# 定义特征和target
cols = [i for i in data.columns if i != 'Price']
label = ['Price']
#数据标准化
lr_data = data
ss = StandardScaler()
lr_data[cols] = ss.fit_transform(lr_data[cols])
#训练模型
lr = LinearRegression()
lr.fit(lr_data[cols],lr_data[label])
#画出特征权重系数值ranking图
plt.figure(figsize = (10,8))
rank_idx = abs(lr.coef_).argsort()
sort_cols = [cols[i] for i in rank_idx[0]]
sort_coef = [lr.coef_.tolist()[0][i] for i in rank_idx[0]]
plt.barh(sort_cols,sort_coef)

由上图可知,影响价格降低的头部因素是低收入人群占比(LSTAT) 和 到市就业中心的距离(DIS),而影响价格升高的头部因素是每栋房屋的平均房间数(RM) 和 到径向公路的可达性系数(RAD)
5.2 基于树模型(LightGBM)的特征重要性
import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import lightgbm as lgb
# 导入数据
data = pd.DataFrame(load_boston()['data'],columns = load_boston()['feature_names'].tolist())
data['Price'] = load_boston()['target']
# 定义特征和target
cols = [i for i in data.columns if i != 'Price']
label = ['Price']
#划分训练集和验证机,防止过拟合
tree_data = data.copy()
X_train, X_val, y_train, y_val = train_test_split(tree_data[cols], tree_data[label], test_size = 0.2, random_state=2022)
#训练模型
model = lgb.LGBMRegressor()
model.fit(X_train,y_train,early_stopping_rounds=10,eval_set=[(X_val,y_val)],verbose=10)
#画出树模型的特征重要性
lgb.plot_importance(model,figsize = (10,8),importance_type = 'split')

由上图可以看出,树模型的特征重要性并没有正负相关影响。从结果上看,与线性回归的前四个特征排名相差无几(RAD换成除了AGE)
5.3 基于SHAP的可解释性
5.3.1 全局解释
#初始化
shap.initjs()
#指定训练好的模型(此处使用上面训练好的LGB)
explainer = shap.Explainer(model)
#指定要计算SHAP的数据
shap_values = explainer(data[cols])
#绘制全局数据点的SHAP值分布图
shap.summary_plot(shap_values,data[cols])
- 颜色表示特征值,红色代表高,蓝色代表低。
- 可以看出当“低收入人群”(LSTAT)越大时,drive房价变低
- 可以看出当“每栋房屋的平均房间数”(RM)越大时,drive房价变高
5.3.2 局部解释
取Price最低的样本做分析
#初始化
shap.initjs()
#指定训练好的模型
explainer = shap.Explainer(model)
#指定要计算SHAP的数据
shap_values = explainer(data[cols])
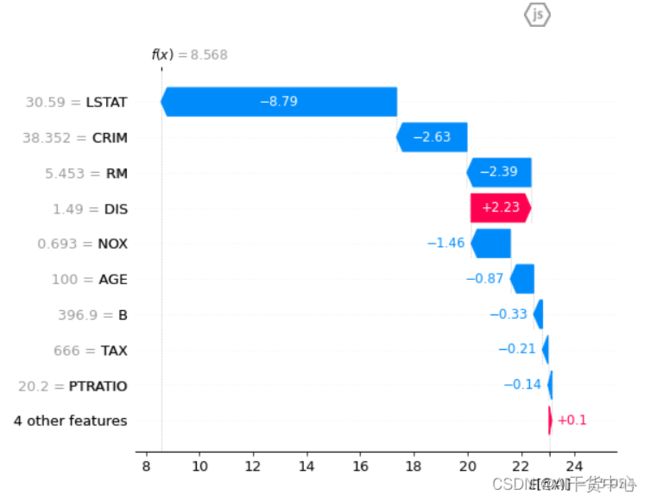
#画出样本中Price最低的SHAP值图
shap.plots.waterfall(shap_values[398])
- 低收入人群占比(LSTAT) 和 犯罪率(CRIM) 成为drive房价变低的头部因素
由数据查之:
- 该样本的犯罪率高达38.51,而所有样本犯罪率均值仅有3.61
- 该样本的低收入人群占比高达30.59,而所有样本低收入人群占比均值仅有12.65
取Price最高的样本做分析
#初始化
shap.initjs()
#指定训练好的模型
explainer = shap.Explainer(model)
#指定要计算SHAP的数据
shap_values = explainer(data[cols])
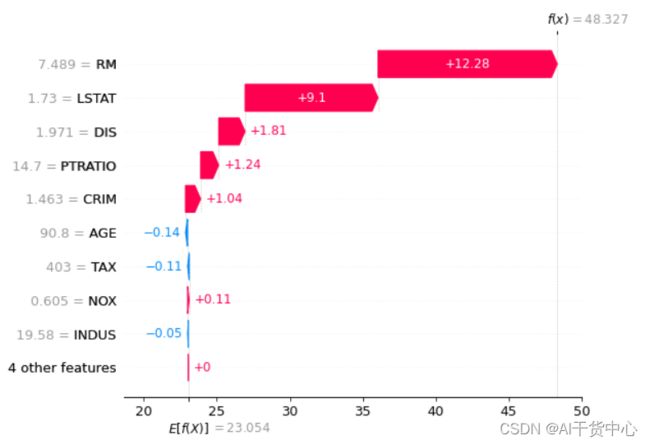
#画出样本中Price最高的SHAP值图
shap.plots.waterfall(shap_values[161])
- 每栋房屋的平均房间数(RM) 和 低收入人群占比(LSTAT) 成为drive房价变高的头部因素
由数据查之:
- 该样本的平均房间数为7.489,而所有样本平均房间数均值为6.28
- 该样本的低收入人群占比为1.73,而所有样本低收入人群占比均值为12.65
5.4 基于LIME的可解释性
5.4.1 局部解释
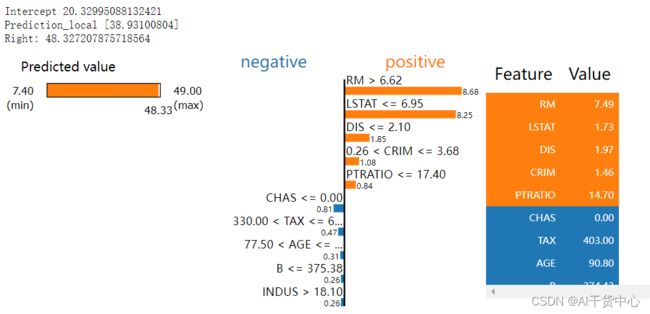
取Price最高的样本做分析
# 导入相关LIME包
from lime.lime_tabular import LimeTabularExplainer
# 指定target + columns + 问题类型(Regression or Classification)
explainer = LimeTabularExplainer(data[cols].values, feature_names = cols,
class_names = label, mode = 'regression',verbose = True)
#指定要分析的案例,此处指定房价最低的样本(index = 161)
exp = explainer.explain_instance(data[cols].iloc[161,:], model.predict)
exp.show_in_notebook(show_table=True)
取Price最低的样本做分析
# 导入相关LIME包
from lime.lime_tabular import LimeTabularExplainer
# 指定target + columns + 问题类型(Regression or Classification)
explainer = LimeTabularExplainer(data[cols].values, feature_names = cols,
class_names = label, mode = 'regression',verbose = True)
#指定要分析的案例,此处指定房价最低的样本(index = 398)
exp = explainer.explain_instance(data[cols].iloc[398,:], model.predict)
exp.show_in_notebook(show_table=True)
- LIME与SHAP的分析结果大同小异
- 在结果细节显示上,LIME更胜一筹,更易读懂
- 在代码复杂度上,SHAP更加清晰明了,封装的更好