机器学习基础:奇异值分解(SVD)
SVD 原理
奇异值分解(Singular Value Decomposition)是线性代数中一种重要的矩阵分解,也是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。
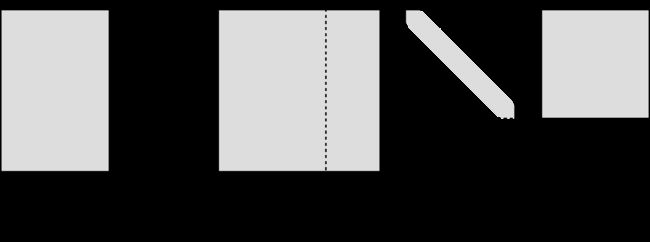
有一个×的实数矩阵,我们想要把它分解成如下的形式: A = U Σ V T A = U\Sigma V^T A=UΣVT
其中和均为单位正交阵,即有 = ^= UUT=I和 = ^= VVT=I,称为左奇异矩阵,称为右奇异矩阵,Σ仅在主对角线上有值,我们称它为奇异值,其它元素均为0。
上面矩阵的维度分别为 U ∈ R m × m U \in R^{m\times m} U∈Rm×m, Σ ∈ R m × n \ \Sigma \in R^{m\times n} Σ∈Rm×n, V ∈ R n × n \ V \in R^{n\times n} V∈Rn×n。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tpOQ6PSy-1650075054769)(https://files.mdnice.com/user/3611/3c237407-033b-4565-ab22-e0fb2e07a9da.svg)]
一般地Σ有如下形式
Σ = [ σ 1 0 0 0 0 0 σ 2 0 0 0 0 0 ⋱ 0 0 0 0 0 ⋱ 0 ] m × n \Sigma = \left[ \begin{matrix} \sigma_1 & 0 & 0 & 0 & 0\\ 0 & \sigma_2 & 0 & 0 & 0\\ 0 & 0 & \ddots & 0 & 0\\ 0 & 0 & 0 & \ddots & 0\\ \end{matrix} \right]_{m\times n} Σ=⎣⎢⎢⎡σ10000σ20000⋱0000⋱0000⎦⎥⎥⎤m×n
Font metrics not found for font: . 越大意味着对应的 ′ ′ A′A 的特征值 σ j 2 \sigma_j^2 σj2 越大, 从而其主成分 (principal component) _ Avj 的样本方差越大, 我们把方差大视为提供了更多信息.
求解U, Σ, V
假设我们的矩阵A是一个m×n的矩阵,则 A T A A^TA ATA是方阵,求其特征值及特征向量:
( A T A ) v i = λ i v i (A^TA)v_i = \lambda_i v_i (ATA)vi=λivi
得到矩阵 A T A A^TA ATA的n个特征值和对应的n个特征向量 v v v
因
A T A = V Σ T U T U Σ V T A^TA=V\Sigma^TU^TU\Sigma V^T ATA=VΣTUTUΣVT = V Σ T Σ V T = V Σ 2 V T V\Sigma^T\Sigma V^T= V\Sigma^2V^T VΣTΣVT=VΣ2VT
将特征向量 v v v张成一个 n × n n×n n×n的矩阵 V V V,就是SVD公式里面的 V V V矩阵, V V V中的每个特征向量叫做 A A A的右奇异向量。
同理: ( A A T ) u i = λ i u i (AA^T)u_i = \lambda_i u_i (AAT)ui=λiui,可得 U U U矩阵。
求得 U , V U , V U,V,然后求Σ,因Σ为奇异值矩阵,所以只需要求出每个奇异值 σ σ σ即可。
$A=U\Sigma V^T \Rightarrow AV=U\Sigma V^TV \Rightarrow $
A V = U Σ ⇒ A v i = σ i u i ⇒ σ i = A v i / u i AV=U\Sigma \Rightarrow Av_i = \sigma_i u_i \Rightarrow \sigma_i=Av_i / u_i AV=UΣ⇒Avi=σiui⇒σi=Avi/ui
其实特征值矩阵等于奇异值矩阵的平方,也就是说特征值和奇异值满足如下关系:
σ i = λ i \sigma_i = \sqrt{\lambda_i} σi=λi
所以不用 σ i = A v i / u i \sigma_i = Av_i / u_i σi=Avi/ui也可以通过求出 A T A A^TA ATA的特征值取平方根来求奇异值。
SVD算法
输入:样本数据
输出:左奇异矩阵,奇异值矩阵,右奇异矩阵
1 计算特征值: 特征值分解 A A T AA^T AAT,其中 A ∈ R m × n A \in \mathbf{R}^{m\times n} A∈Rm×n为原始样本数据
A A T = U Σ Σ T U T AA^T=U\Sigma \Sigma^TU^T AAT=UΣΣTUT
得到左奇异矩阵 U ∈ R m × m U \in \mathbf{R}^{m \times m} U∈Rm×m和奇异值矩阵 Σ ′ ∈ R m × m \Sigma' \in \mathbf{R}^{m \times m} Σ′∈Rm×m
2 间接求部分右奇异矩阵: 求 V ′ ∈ R m × n V' \in \mathbf{R}^{m \times n} V′∈Rm×n
利用A=UΣ′V′可得
V ′ = ( U Σ ′ ) − 1 A = ( Σ ′ ) − 1 U T A V' = (U\Sigma')^{-1}A = (\Sigma')^{-1}U^TA V′=(UΣ′)−1A=(Σ′)−1UTA
3 返回U, Σ′, V′,分别为左奇异矩阵,奇异值矩阵,右奇异矩阵。
Python 求解SVD
from numpy import array
from numpy import diag
from numpy import zeros
from scipy.linalg import svd
# define a matrix
A = array([
[1,2,3,4,5,6,7,8,9,10],
[11,12,13,14,15,16,17,18,19,20],
[21,22,23,24,25,26,27,28,29,30]])
print(A)
>>> A
array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[11, 12, 13, 14, 15, 16, 17, 18, 19, 20],
[21, 22, 23, 24, 25, 26, 27, 28, 29, 30]])
# Singular-value decomposition
U, s, VT = svd(A)
# create m x n Sigma matrix
Sigma = zeros((A.shape[0], A.shape[1]))
# populate Sigma with n x n diagonal matrix
Sigma[:A.shape[0], :A.shape[0]] = diag(s)
# select
n_elements = 2
Sigma = Sigma[:, :n_elements]
VT = VT[:n_elements, :]
# reconstruct
B = U.dot(Sigma.dot(VT))
print(B)
>>> B
array([[ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.],
[11., 12., 13., 14., 15., 16., 17., 18., 19., 20.],
[21., 22., 23., 24., 25., 26., 27., 28., 29., 30.]])
# transform
T = U.dot(Sigma)
print(T)
>>> T
array([[-18.52157747, 6.47697214],
[-49.81310011, 1.91182038],
[-81.10462276, -2.65333138]])
T = A.dot(VT.T)
print(T)
[[-18.52157747 6.47697214]
[-49.81310011 1.91182038]
[-81.10462276 -2.65333138]]
参考:
https://www.cnblogs.com/pinard/p/6251584.html
https://www.cnblogs.com/endlesscoding/p/10033527.html