数学建模心得分享(校赛)——2021.6.7

 一、个人感受

  总结为：找队友->讲方法->找知识->善讨论->勤实践

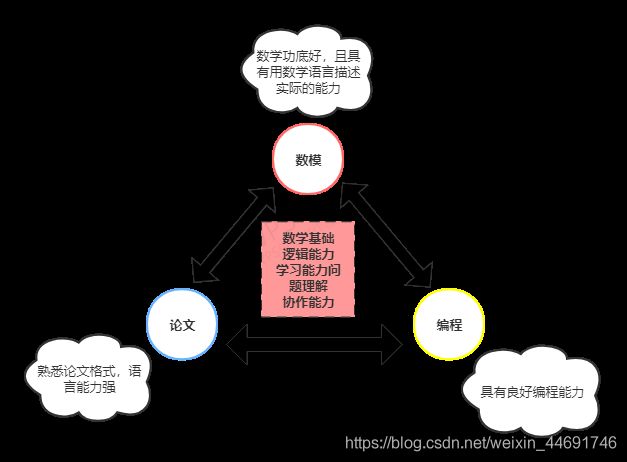
  基础能力(个人见解)：

  第一次比赛完，还有这刚刚实习完的余温，工作中的思维的惯性还时刻在影响着我，身边的人几乎都为了自己的生活而奋斗。有幸参加能参加这次比赛，其实当初也是冲着能够锻炼逻辑思维和团队协作能力去的。

  最初，我找到了许多优秀的文章以及和往届的参赛同学以此来交流和学习，有幸认识到我的两位学妹作为组员(最好是三不同(专业，年纪，性别)，这可能更类似以后现实中的团队场景，更加多元化。

  校赛(7天左右)的起初，由于他们比较忙，给我泼了一盆冷水(前期几乎没法投入比赛中来)，我渐渐开始意识到，寻找团队里的队员也是很需要技巧和经验的，我当初还是凭着感觉和交流能力去寻找的，这一点让我涨了教训，真的需要组员之间通力合作，有默契的队伍才会有动力在比赛中坚持下去。小组内互相认识、互相了解才会在最累的时候互相支持。一个队伍需要的是你认可的凝聚力，而不是有一个人专门端茶倒水。而且学习了解一个人对于团队是否绝对忠诚；能否有自己独立思维能力；以及强大的执行力真的很难也很重要，(1+1>2)这种事真的几乎只会发生在真正的团队上，所以，这本来是前期最重要的准备工作(当初并没有太当回事)，这里我建议比赛前，大家先线下见次面，也算一次为了交友的团建，可以随便聊一聊，这真的可以大概知道他在比赛中的状态，我并没有责备她们的意思，只不过是感到有些惋惜。 

  说白了就是，你能否有效判断，你的组员你的团队是否可以为了比赛去付出相对富裕的时间和经历，而不是大家都把活二推来推去，这是基础，也是比赛的通病。

  我认为真正的意义上的躺赢，是丝毫没有意义的，真么着你也得整点你满意的东西。

  可能因为我是学长又加上唯一个男孩儿(无非就是心理更成熟)，就成为了队伍的组长，我的起初目标是将这一周的时间充分利用起来，做到每天按步走，让大家更能多方面的感受每个过程的目的，这样也可以让大家每天去总结和规划我们的思维和经验，而不是两天敢出来一个作品。一定不要让大家产生不平等的感觉，组长只是在这个比赛中起到了引领的作用，仅仅是带动大家，给大家提供一个大概的方向，当然，我觉得一定要多多学习思维力和心理学。这回涉及到你生活的方方面面。

  上面提及的也是我感同身受的，尤其是当我兴致勃勃的将比赛做了一个比较充足的规划，安排了很基础的任务，和她们分享了我的经验之后，我收到的反馈却是，疑惑和无感...(这里我意识到学习能力和热情的重要性)

  经过我不懈的努力，我在比赛这一周当中有幸约到了她们俩各一次，每次都会提前说到开会的原因和目的，这点我认为很有必要，要不然，开会干嘛啊，就让你干讲吗？(结果还是我一个人干说...) 还有，一定要带纸和笔！边讨论边记录。（这里我意识到大家一定要具备一定的基础知识和讨论协商能力）

  其实看到这里，你可能已经猜到了这次比赛我们一定会很差很差，最后提交论文的时候，我还有一丝不甘心，明明可能会小有成果，却发生了这样的收尾...我很平凡，但是我不甘平庸。

  比赛结束后，我反思到，我所谓的科学理论为什么没有成功是因为他根本不适合我所组建的团队，我可能从第一步就错了，比赛的成绩真的不重要，重要的是锻炼到了你的什么能力，发现你的不足，需要侧重补充什么。

  数学比赛其实特别切合实际，这是一个人可以受益终身的工具，在如今信息如此爆炸的时代，当你可以处理分析大量数据，并得到一些优化的方法，这价值真的太必要了。

  相信我，从现在开始动手去套索吧~

  明年我必将从新参赛，到时候我可能不会成为队长，我可能只是一位普通的组员，但我必将为了自己的信念和目标继续奋斗！！！

其实很多优秀的论文，其高明之处并不是用了多少数学知识，而是思维比较全面、贴合实际、能解决问题或是有所创新。

---

二、比赛思路

  我的思路主要是来自于网络上文章和以及同学的交流，主要思路:

1. 提出问题(知识的匹配和延申)：

(1)每位组员都需把比赛问题弄懂，在转化成自己整理出来的问题(尽量用数学语言表达)。

(2)组员统一符号，交流对问题的看法，尽量多开会，组长开会前一定要安排好会议的目的和目标，写出来，同步给组员(节约大家时间)。

(3)可以模拟建模，也方便后续思考整理

1. 寻找建模方法(先问清楚自己第一步完成的咋样)：

(1)每位组员都需自己寻找文献(工作量大，但是关键)，可以多维度寻找，有关联即可。

(2)多翻一翻《数学模型(姜启源、谢金星)》,会产生灵感。

1. 推导模型公式(需要大量的2作为基础):

(1)对1和2的实现（模子和原料=>制作成品）。参考文献做修改。

(2)团队统一，把每个人的建议参考，采纳，过滤，优化。

1. 求解模型(对3的实现)

(1)组员都需要掌握或熟悉一些计算机语言的使用。

(2) Matlab(微分方程，运筹规划，智能算法，图像处理)是必须的，再有SPSS(统计模型)，足以。

1. 回答问题(1-4的思路概述和总结)

1. 论文的讨论部分，写的要有深度，可能需要图表，思维导图（XMind）等等。

---

三、工具

这些是一些可能用到的工具

• - 编程工具（Matlab / Python / Mathematica ）
• - 统计建模（R / SPSS / Minitab）
• - 论文写作（Word / LaTex）
• - 公式编辑器（MathType）
• - 插图制作（PowerPoint / PS）
• - 流程图绘制（Visio）
• - 版本控制器（SVN / Git）
• - 团队资料笔记共享（有道云笔记）

 

模型大致类型：

• 一、优化类
• 线性规划（运输问题、指派问题、对偶理论、灵敏度分析）
• 整数规划（分支定界、枚举试探、蒙特卡洛）
• 非线性规划（约束极值、无约束极值）
• 目标规划（单目标、多目标）
• 动态规划（动态、静态、线性动规、区域动规、树形动规、背包动规）
• 动态优化（变分法）
• 现代优化算法（贪婪算法、禁忌搜索、模拟退火、遗传算法、人工神经网络、蚁群算法、粒子群算法、人群搜索算法、人工免疫算法、集成算法、TSP问题、QAP问题、JSP问题）
• 模糊逼近算法
•  
• 二、图论
• 最小生成树（prim算法、Kruskal算法）
• 最短路径（Dijkstra算法、Floyd-Warshall算法、Bellman-Ford算法、SPFA算法）
• 匹配问题（匈牙利算法）
• Euler图和Hamilton图
• 网络流（最大流问题、最小费用最大流问题）
•  
• 三&四、预测类&统计
• GM（1，1）灰度预测
• 时间序列模型（确定性时间序列、平稳时间序列、移动平均、指数平滑、Winter方法、ARIMA模型）
• 回归（一元线性回归、多元线性回归MLR、非线性回归、多元逐步回归MSR、主元回归法PCR、部分最小二乘回归法PLSR）（重点）
• Bayes统计预测
• 分类模型（逻辑回归、决策树、神经网络）
• 判别分析模型（距离判别、Fisher判别、Bayes判别）
• 参数估计（点估计、极大似然估计、Bayes估计）
• 假设检验（U-检验、T-检验、卡方检验、F-检验、最优性检验、分布拟合检验）
• 方差分析（单因素、多因素、相关性检验）
• 经验分布函数
• 正交试验
• 模糊数学（模糊分类、模糊决策）
• 随机森林
•  
• 五、数据处理
• 图像处理
• 插值与拟合（Lagrange插值、Newton插值、Hermite插值、三次样条插值、线性最小二乘）
• 搜索算法（回溯、分治、排序、网格、穷举）
• 数值分析方法（方程组求解、矩阵运算、数值积分、逐次逼近法、牛顿迭代法）
• 模糊逼近
• 动态加权
• ES
• DWRR
• 序列分析
• 主成分分析
• 因子分析
• 聚类分析
• 灰色关联分析法
• 数据包络分析法（DEA）
•  
• 六、评价类
• 层次分析法（AHP）
• 模糊综合评价
• 基于层次分析的模糊综合评价
• 动态加权综合评价
• TEIZ理论
•  
• 七、图形类（重点）
• 算法流程图
• 条形图
• 直方图
• 散点图
• 饼图
• 折线图
• 茎叶图
• 箱线图
• P_P图
• Q_Q图
• Venn图
• 矢量图
• 误差分析图
• 概率分布图
• 5w1h分析法
• 漏斗模型
• 金字塔模型
• 鱼骨分析法
• 等高线曲面图
• 思维导图
•  
• 八、模拟与仿真
• 蒙特卡洛
• 元胞自动机
•  
• 九、方程（进阶）
• 微分方程（Malthus人口模型、Logistic模型、战争模型）
• 稳定状态模型（Volterra 模型）
• 常微分方程的解法（离散化、Euler方法、Runge—Kutta方法、线性多步法）
• 差分方程（蛛网模型、遗传模型）
• 偏微分方程数值解（定解问题、差分解法、有限元分析）
•  
• 十、数据建模&机器学习方法（当前热点）
• （注：此部分与数据处理算法有大量重叠）
• 云模型
• Logistic回归
• 主成分分析
• 支持向量机（SVM）
• K-均值（K-Means）
• 近邻法
• 朴素Bayes判别法
• 决策树方法
• 人工神经网络（BP、RBF、Hopfield、SOM）
• 正则化方法
• kernel算法
•  
• 十一、其他
• 排队论
• 博弈论
• 贮存伦
• 概率模型
• 马氏链模型
• 决策论
• （单目标决策：不确定型决策、风险决策、效用函数、决策树、灵敏度分析）
• （多目标决策：分层序列法、多目标线性规划、层次分析法）
• 系统工程建模（ISM解释模型、网络计划模型、系统评价、决策分析）
• 交叉验证方法（Holdout 验证、K-fold cross-validation、留一验证）

有任何想法和指正的地方欢迎留言讨论

参考： 如何入门参与数学建模？_JiandaoStudio-CSDN博客_数学建模学习