最大网络流算法之dinic算法

---

最大网络流

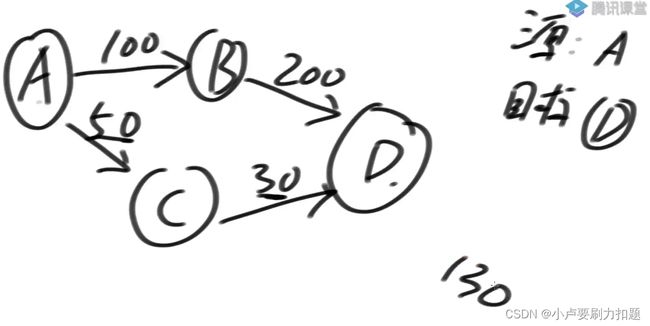
首先要给出每一条线路的承载量,一定要把边都是有方向的。一定要指明一个源点跟目标点如图源点是A,目标点是D,如果从A点灌水,没一根关系都有它的承载量,问从A出发能灌多少水到D,整个流最大是多少?

深度优先搜索

朴素的深度优先遍历不行,会因为选边的顺序导致算不出正确答案

Dinic

Dinic算法的主线
它最普遍的一点就是它有一个负反馈路线,或者说他有一个隐含的路线。

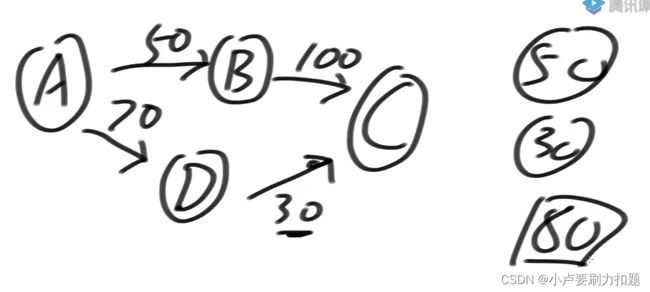
如图最大流量为80

补反向边,也就是说你减少多少,你的反向边就增加多少
补反向边,不会让总答案变大,但是能解决反悔的问题

如果你是正常线路的话,增加反向边不会增大答案,但是会因此让已经错失的可能性给报回来

第一个优化:高度数組

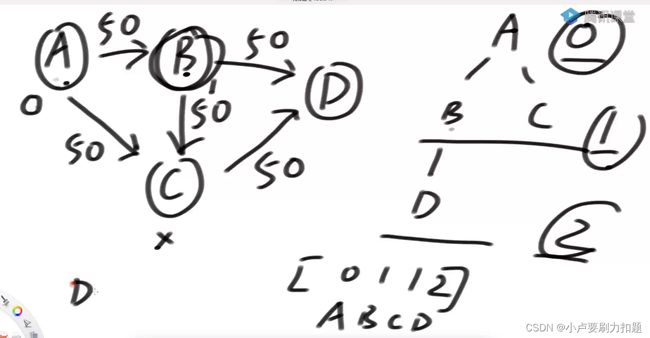
建立高度,让我每一步往下推的代价,尽量的低
从A出发完宽度优先遍历。认为A的高度是0, BC的高度是1,D的高度是2
我有一个数组记录的每一个点的层数
当我这个A往下走的时候,只有层数变大的路我去选。
A到B能不能到?能到,A是0层B是1层,而且层数大了1
从B走的时候,B要不要到C层?不要,因为你俩层数一样,本身Dinic算法规避了回去的问题。
所以B发现C跟自己层数一样,这条路它就不会走,它直接从A到B到D,一条深度优先,然后从A到C到D
先建立起1个高度数组,玩DFS这样的一种机制本身可以避免来回走的问题。

第二个优化

有一个支路数组,记录着每一个点走到了哪条支路了
记录哪些数组用过了,不用再尝试

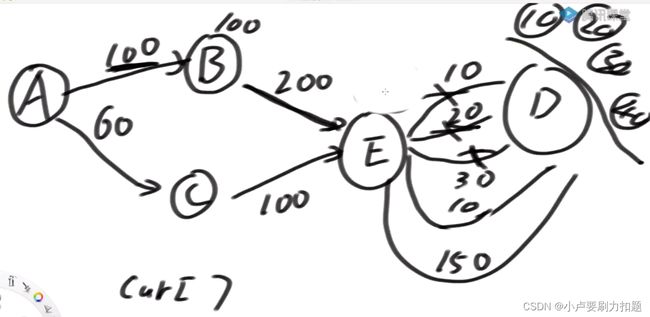
例如我们从a到d,其中第一条支路A->B->E->D 其中50这条支路还剩10,上面的支路已经走完了,不能再走了

接下来,A选择第二条线路如果我们有一个数组记录着某一个点之前哪些线路用过了,此时我就不用再看10用不用,20用不用,30用不用它们都跳过了,直接从没用完的边继续试。

二、代码

1城市拥有哪些边是一个list(),里头是边的编号每一个城市拥有边的编号,它其实在边数组里去找。
城市拥有哪些边是边的编号,这样有两个好处:
1.不影响我城市的跳转2.0,1 2,3 4,5…
一条边进来生成两条进入边数组里去,所以0,1互成反向,2,3互成反向,4,5互成反向号边的反向边就是i^1,特别方便找反向

	public static class Edge {
		public int from;
		public int to;
		public int available;

		public Edge(int a, int b, int c) {
			from = a;
			to = b;
			available = c;
		}
	}

	public static class Dinic {
		private int N;
		private ArrayList<ArrayList<Integer>> nexts;
		private ArrayList<Edge> edges;
		private int[] depth;
		private int[] cur;

		public Dinic(int nums) {
			N = nums + 1;
			nexts = new ArrayList<>();
			for (int i = 0; i <= N; i++) {
				nexts.add(new ArrayList<>());
			}
			edges = new ArrayList<>();
			depth = new int[N];
			cur = new int[N];
		}

		public void addEdge(int u, int v, int r) {
			int m = edges.size();
			edges.add(new Edge(u, v, r));
			nexts.get(u).add(m);
			edges.add(new Edge(v, u, 0));
			nexts.get(v).add(m + 1);
		}

		public int maxFlow(int s, int t) {
			int flow = 0;
			while (bfs(s, t)) {
				Arrays.fill(cur, 0);
				flow += dfs(s, t, Integer.MAX_VALUE);
				Arrays.fill(depth, 0);
			}
			return flow;
		}

		private boolean bfs(int s, int t) {
			LinkedList<Integer> queue = new LinkedList<>();
			queue.addFirst(s);
			boolean[] visited = new boolean[N];
			visited[s] = true;
			while (!queue.isEmpty()) {
				int u = queue.pollLast();
				for (int i = 0; i < nexts.get(u).size(); i++) {
					Edge e = edges.get(nexts.get(u).get(i));
					int v = e.to;
					if (!visited[v] && e.available > 0) {
						visited[v] = true;
						depth[v] = depth[u] + 1;
						if (v == t) {
							break;
						}
						queue.addFirst(v);
					}
				}
			}
			return visited[t];
		}

		// 当前来到了s点，s可变
		// 最终目标是t，t固定参数
		// r，收到的任务
		// 收集到的流，作为结果返回，ans <= r
		private int dfs(int s, int t, int r) {
			if (s == t || r == 0) {
				return r;
			}
			int f = 0;
			int flow = 0;
			// s点从哪条边开始试 -> cur[s]
			for (; cur[s] < nexts.get(s).size(); cur[s]++) {
				int ei = nexts.get(s).get(cur[s]);
				Edge e = edges.get(ei);
				Edge o = edges.get(ei ^ 1);
				if (depth[e.to] == depth[s] + 1 && (f = dfs(e.to, t, Math.min(e.available, r))) != 0) {
					e.available -= f;
					o.available += f;
					flow += f;
					r -= f;
					if (r <= 0) {
						break;
					}
				}
			}
			return flow;
		}
	}

	public static void main(String[] args) {
		Scanner cin = new Scanner(System.in);
		int cases = cin.nextInt();
		for (int i = 1; i <= cases; i++) {
			int n = cin.nextInt();
			int s = cin.nextInt();
			int t = cin.nextInt();
			int m = cin.nextInt();
			Dinic dinic = new Dinic(n);
			for (int j = 0; j < m; j++) {
				int from = cin.nextInt();
				int to = cin.nextInt();
				int weight = cin.nextInt();
				dinic.addEdge(from, to, weight);
				dinic.addEdge(to, from, weight);
			}
			int ans = dinic.maxFlow(s, t);
			System.out.println("Case " + i + ": " + ans);
		}
		cin.close();
	}