常见的链表面试题

常见的链表面试题

设计一个链表

typedef struct Node
{
	int data;
	struct Node* next;
}Node;

typedef struct List
{
	Node* head;	 //头指针
	Node* tail;  //尾指针
	size_t size; //节点个数
}List;

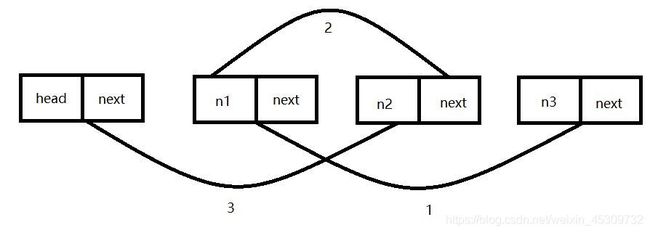
1、链表逆序

（不是改变值，改指针指向，要求不使用额外空间）

int reverse_list(List* list)
{
	Node* tmp = NULL;
	Node* cur = list->head->next;
	if(!cur) return -1;
	while(!list->tail->next)
	{
		tmp = cur->next;
		cur->next = tmp->next;
		tmp->next = list->head->next;
		list->head->next = tmp;
	}
	return 0;
}

2、找出链表中的倒数第n个节点

​ 1、遍历一次计算长度len,第二次遍历找到len-n+1的节点返回，浪费时间，略

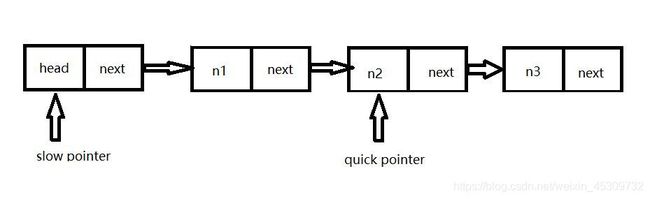
​ 2、利用快慢指针，快指针一个先走n-1步，慢指针再开始从头节点走，当快指针到达结尾时，慢指针刚好指向倒数第n个

int find(List* list,int n)
{
	Node* q = list->head;
	Node* s = list->head;
	for(int i=0;i<=n-1;i++) q = q->next;
	while(q->next != NULL)
	{
		q = q->next;
		s = s->next;
	}
	return s->next->data;
}

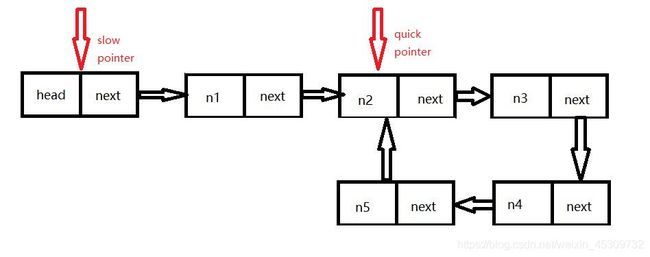
3、判断单链表是否存在环

​ 利用快慢指针判断是否相遇，相遇则有环

bool Isloop(List* list)
{
	if(list->head == NULL) return false;
	Node* slow = list->head->next;
	Node* quick = slow->next;
	while(slow != NULL && quick != NULL)
	{
		if(slow == quick) return true;
		slow = slow->next;
		quick = quick->next;
		if(quick != NULL) quick = quick->next;
	}
	return false;
}

4、找出环形链表的入口

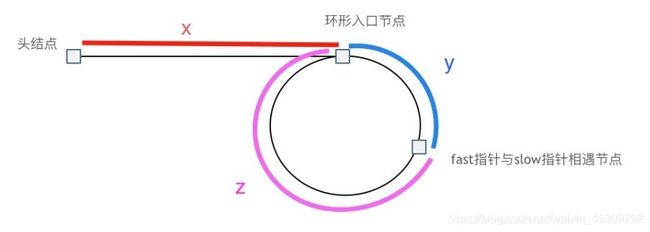
​ 利用上面的方法可以判断是否有环后，我们先推到一下快慢指针间的结点关系(慢指针一次走一步，快指针一次走两步)

​ x:从头结点到环形入口节点 的节点数为

​ y:环形入口节点到 fast指针与slow指针相遇节点 节点数为

​ z:从相遇节点 再到环形入口节点节点数为

​ 当快慢指针相遇时，慢指针走过了 x+y 个节点，快指针走过了 x+y+n(z+y)

​ 由步长可以得出 2(x+y ) = x+y+n(z+y) 推导出 x = (n - 1) (y + z) + z

​ 当n = 1 时候 推导出 x = z

​ 这就意味着，从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候

​ 就是环形入口的节点。

​ 当快慢指针相遇时我们定义一个 index1 从相遇节点出发, index2从头节点出发，他两相遇时index1即为环的入口

int find_enter(List* list)
{
	Node* fast = list->head;
	Node* slow = list->head;
	while(fast != NULL && fast->next != NULL)
	{
		slow = slow->next;
		fast = fast->next->next;
		if(slow == fast)
		{
			Node* index1 = fast;
			Node* index2 = list->head;
			while(index1 != index2)
			{
				index1 = index1->next;
				index2 = index2->next;
			}
			return index2->data;
		}
	}
	return 0;
}

5、合并两个有序的链表，合并后依然有序

​ 1、创建一个新的链表然后对两个链表排序，放入新的链表中

​ 2、直接将L2添加到L1后面去，整体排序

ListNode* ReNewCombineList(ListNode* p1, ListNode* p2)
{
    ListNode* pNewList = NULL;
    //ListNode* p3 = NULL;
    if (p1 == NULL)
        return p2;
    if (p2 == NULL)
        return p1;
    if (p1->data < p2->data)
    {
        pNewList = p1;
        pNewList->next = ReNewCombineList(p1->next, p2);
    }
    else
    {
        pNewList = p2;
        pNewList->next = ReNewCombineList(p1, p2->next);
    }
    return pNewList;
}

6、判断两个链表是否是Y型链表

​ 1、先访问其中一个链表，在每访问一个节点时，都对另外一个链表进行遍历，看节点是否相等，直到找到一个相等的节点位置，如果链表长度分别是m,n 则时间复杂度为O(mn)

​ 2、我们可以知道如果两个链表有公共节点，那么该公共节点之后的所有节点都是两个链表所共有的，所以长度一定也是相等的，如 果两个链表的总长度是相等的，那么我们对两个链表进行遍历，则一定同时到达第一个公共节点。但是链表的长度实际上不一定相同， 所以我们只需要计算出两个链表的长度之差n，然后让长的那个链表先移动n步，短的链表再开始向后遍历，这样他们一定同时到达第 一个公共节点，我们只需要在向后移动的时候比较两个链表的节点是否相等就可以获得第一个公共节点。时间复杂度是O(m+n)

​ 3、我们可以将其中一个链表的首尾相连，然后判断另一个链表是否含环。如果含环，则两链表交叉；否则，不交叉。时间复杂度是 O(max[m,n])