斯坦福NLP名课带学详解 | CS224n 第8讲 - 机器翻译、seq2seq与注意力机制（NLP通关指南·完结）

• 作者：韩信子@ShowMeAI，路遥@ShowMeAI，奇异果@ShowMeAI
• 教程地址：http://www.showmeai.tech/tutorials/36
• 本文地址：http://www.showmeai.tech/article-detail/243
• 声明：版权所有，转载请联系平台与作者并注明出处
• 收藏ShowMeAI查看更多精彩内容

---

ShowMeAI为斯坦福CS224n《自然语言处理与深度学习(Natural Language Processing with Deep Learning)》课程的全部课件，做了中文翻译和注释，并制作成了GIF动图！

本讲内容的深度总结教程可以在这里 查看。视频和课件等资料的获取方式见文末。

---

引言

本篇内容覆盖

• 引入新任务：机器翻译
• 引入一种新的神经结构：sequence-to-sequence
  • 机器翻译是 sequence-to-sequence 的一个主要用例
• 引入一种新的神经技术：注意力
  • sequence-to-sequence 通过 attention 得到提升

1.机器翻译与SMT（统计机器翻译）

1.1 Pre-neural Machine Translation

1.2 机器翻译

机器翻译(MT)是将一个句子 $x$ 从一种语言(源语言)转换为另一种语言(目标语言)的句子 $y$ 的任务。

1.3 1950s：早期机器翻译

机器翻译研究始于20世纪50年代初。

• 俄语 → 英语(冷战的推动)
• 系统主要是基于规则的，使用双语词典来讲俄语单词映射为对应的英语部分

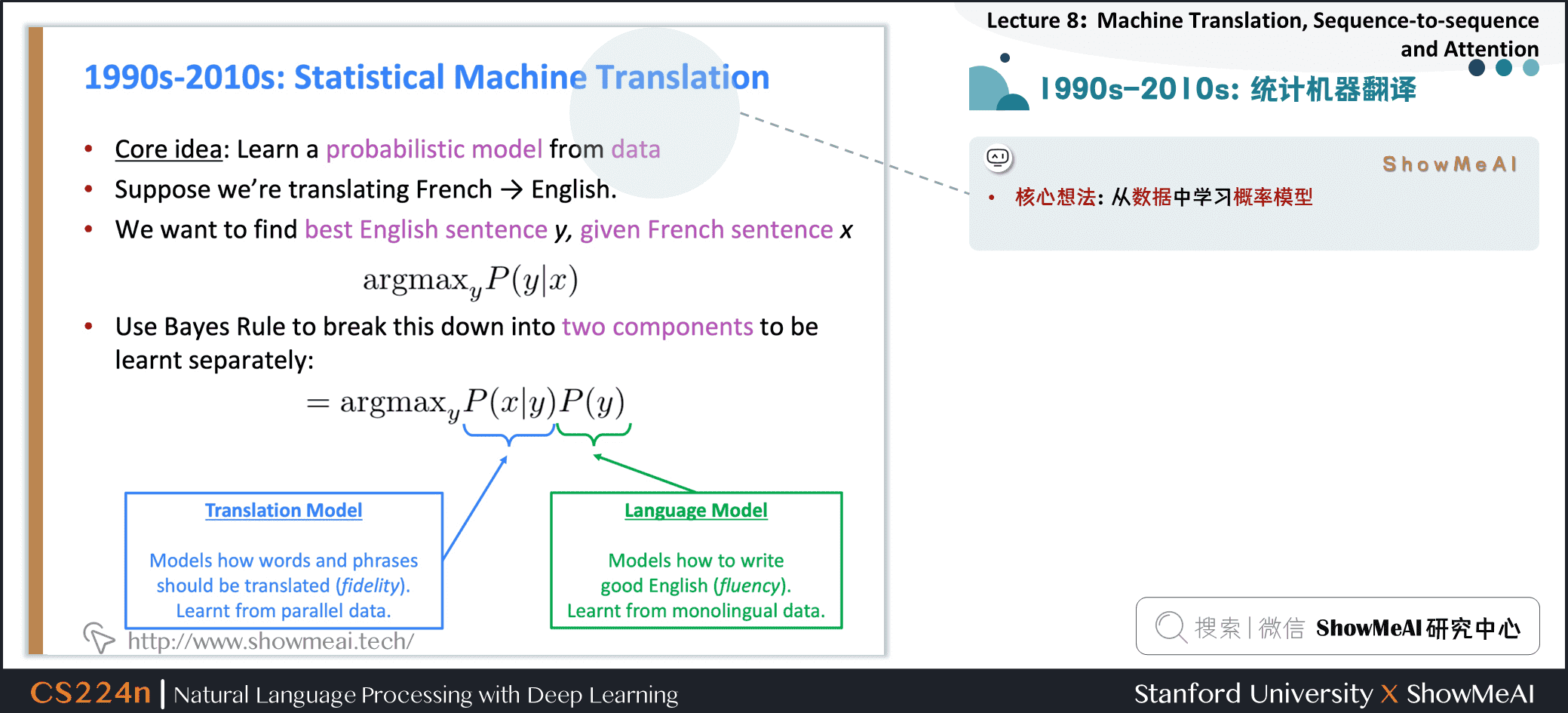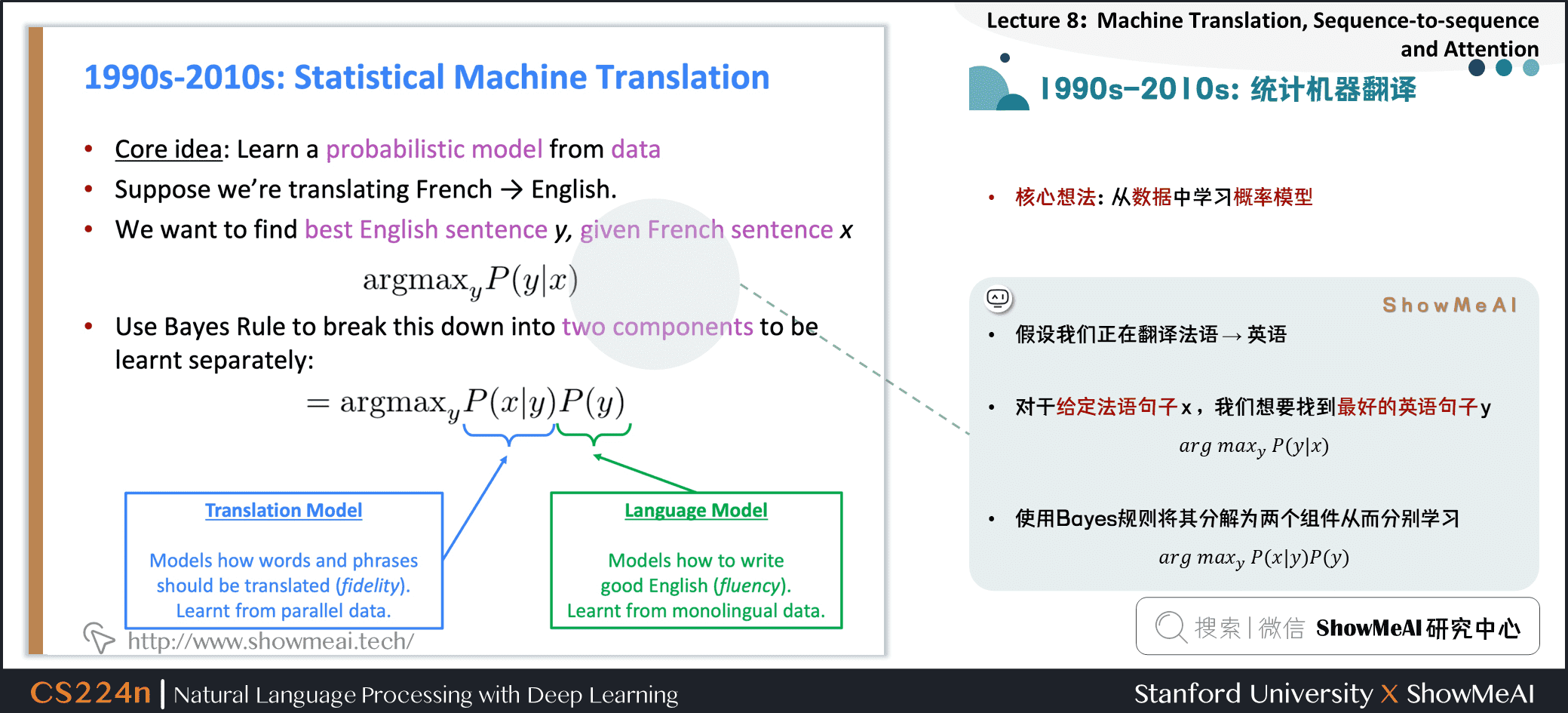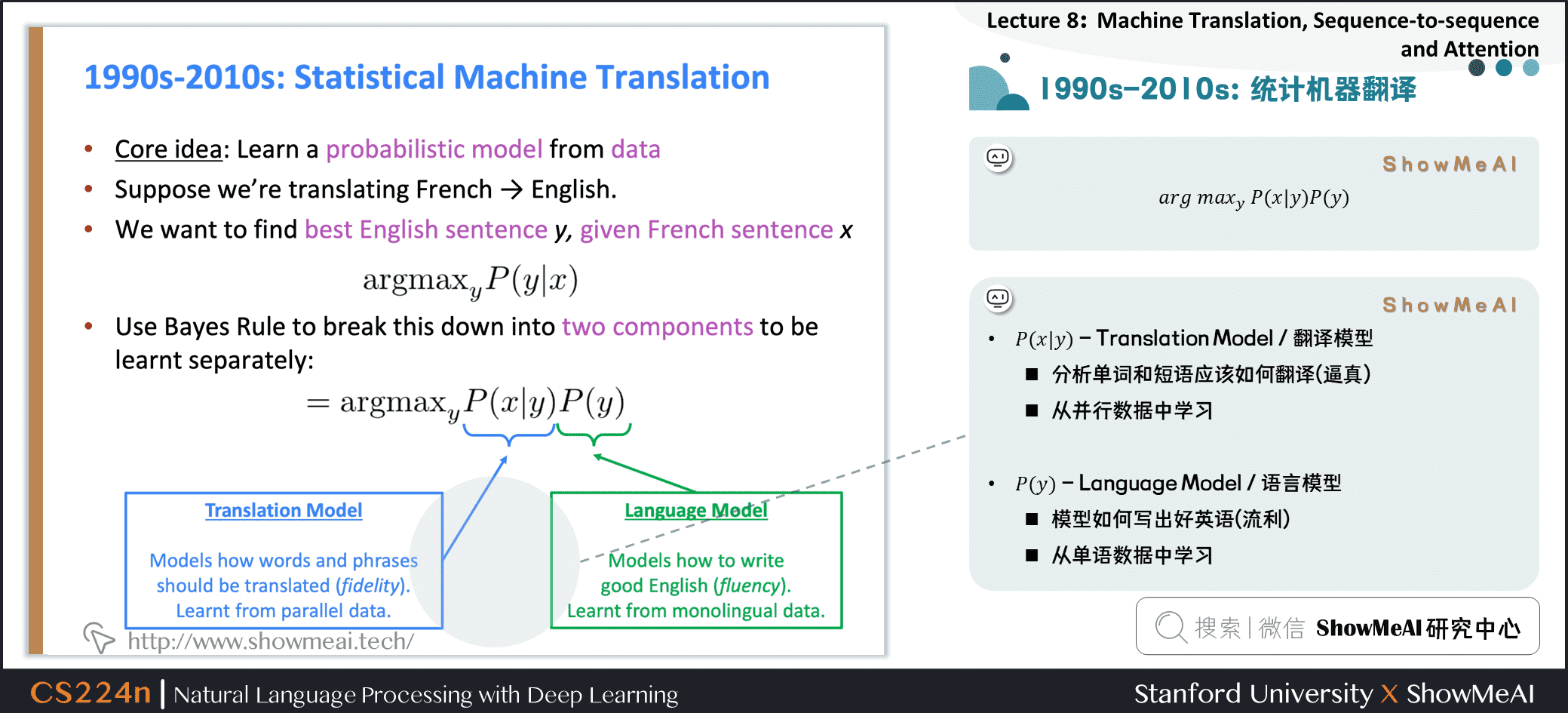
1.4 1990s-2010s：统计机器翻译

• 核心想法：从数据中学习概率模型

• 假设我们正在翻译法语 → 英语

• 对于给定法语句子 $x$，我们想要找到最好的英语句子 $y$

$$argma{x}_{y}P(y\mid x)$$

• 使用Bayes规则将其分解为两个组件从而分别学习

$$argma{x}_{y}P(x\mid y)P(y)$$

• $P(x\mid y)$：Translation Model / 翻译模型

  • 分析单词和短语应该如何翻译(逼真)
  • 从并行数据中学习

• $P(y)$：Language Model / 语言模型

  • 模型如何写出好英语(流利)
  • 从单语数据中学习

1.5 1990s-2010s：统计机器翻译

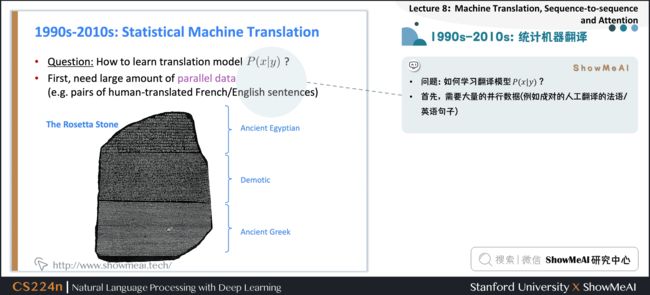
• 问题：如何学习翻译模型 P(x \mid y)？

• 首先，需要大量的并行数据(例如成对的人工翻译的法语/英语句子)

1.6 SMT的学习对齐

• 问题：如何从并行语料库中学习翻译模型 $P(x\mid y)$？
• 进一步分解：我们实际上想要考虑

$$P(x,a\mid y)$$

• $a$ 是对齐
• 即法语句子 $x$ 和英语句子 $y$ 之间的单词级对应

1.7 对齐

Examples from: “The Mathematics of Statistical Machine Translation: Parameter Estimation", Brown et al, 1993. http://www.aclweb.org/anthology/J93-2003

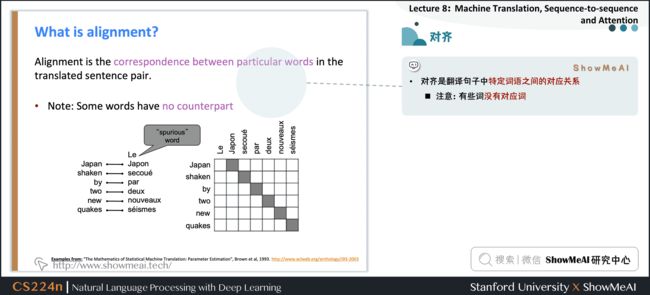
• 对齐是翻译句子中特定词语之间的对应关系
  • 注意：有些词没有对应词

1.8 对齐是复杂的

• 对齐可以是多对一的

1.9 对齐是复杂的

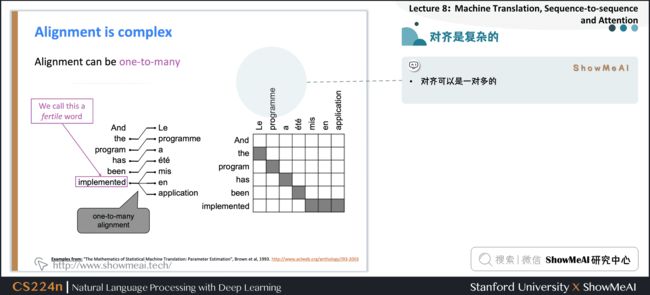
• 对齐可以是一对多的

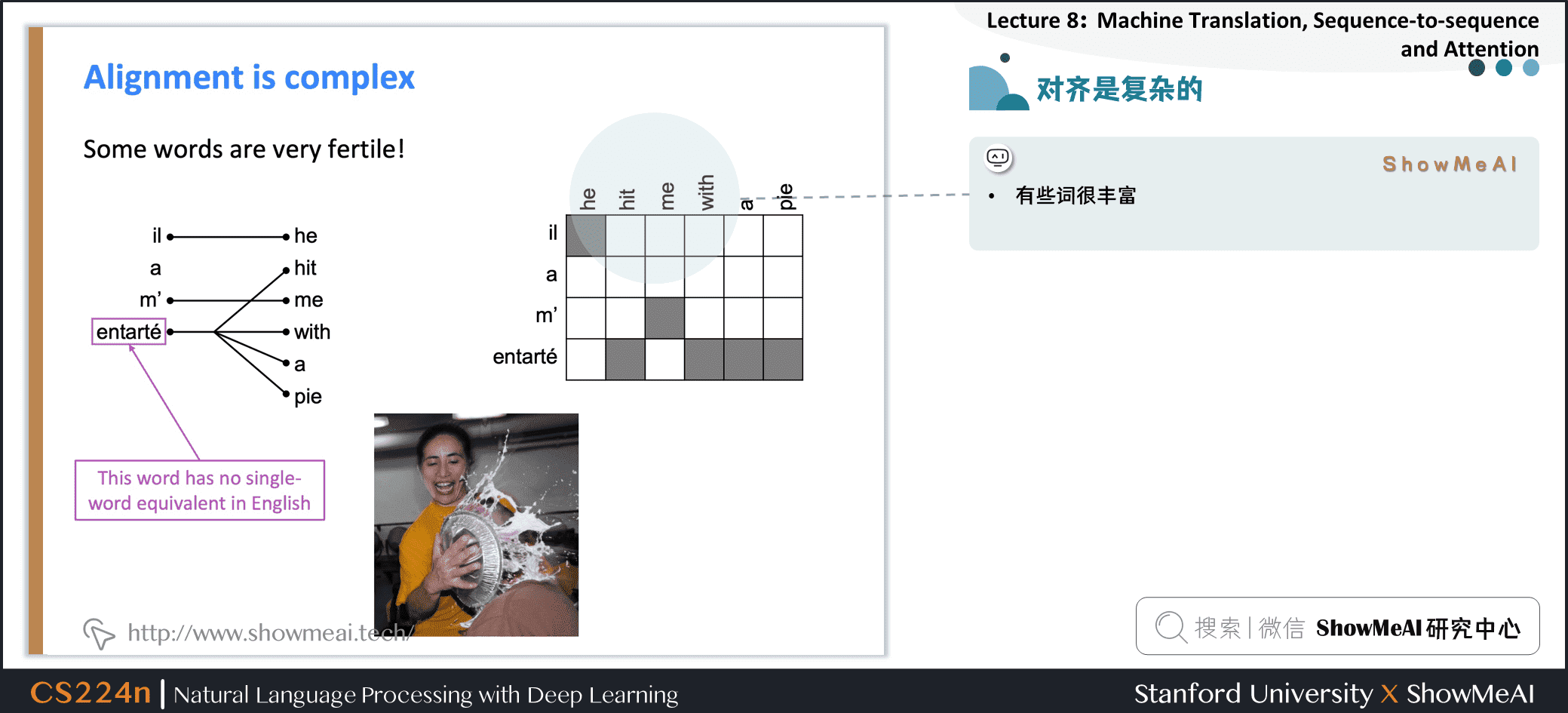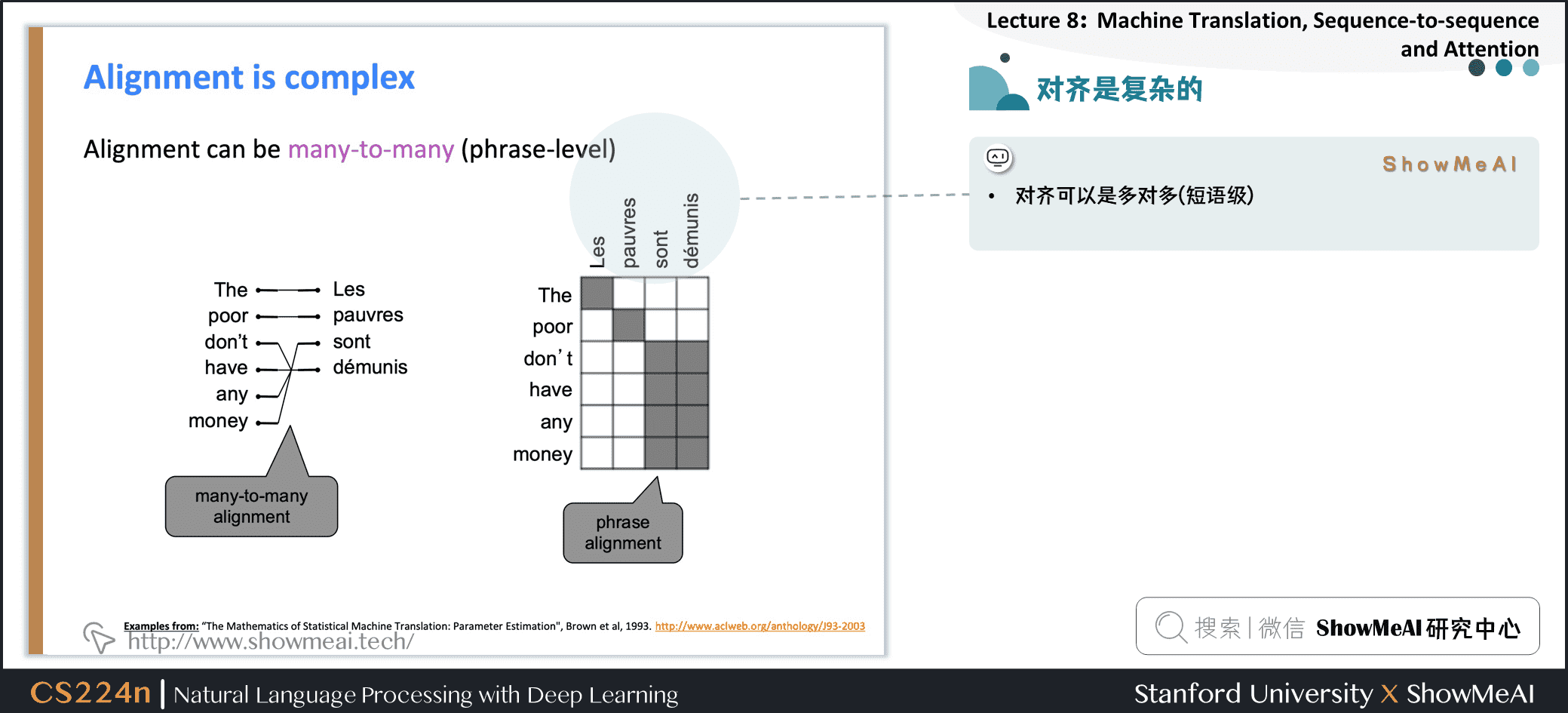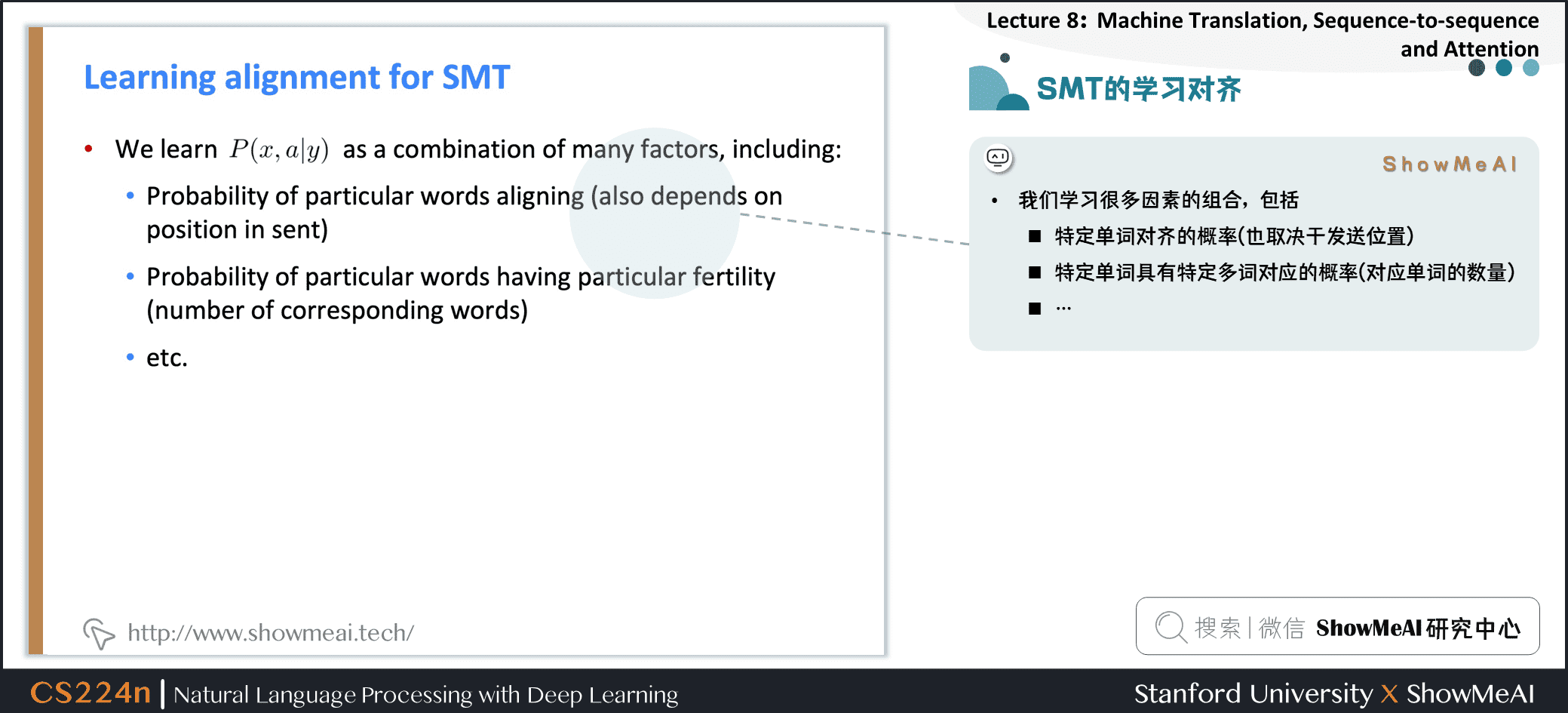
1.10 对齐是复杂的

• 有些词很丰富

• 对齐可以是多对多(短语级)

• 我们学习很多因素的组合，包括

  • 特定单词对齐的概率(也取决于发送位置)
  • 特定单词具有特定多词对应的概率(对应单词的数量)

1.11 SMT的学习对齐

• 问题：如何计算argmax

  • 我们可以列举所有可能的 $y$ 并计算概率？→ 计算成本太高

• 回答：使用启发式搜索算法搜索最佳翻译，丢弃概率过低的假设

  • 这个过程称为解码

1.12 SMT解码

Source: ”Statistical Machine Translation", Chapter 6, Koehn, 2009. https://www.cambridge.org/core/books/statistical-machine-translation/94EADF9F680558E13BE759997553CDE5

1.13 SMT解码

1.14 1990s-2010s：统计机器翻译

• SMT是一个巨大的研究领域

• 最好的系统非常复杂

  • 数以百计的重要细节我们还没有提到
  • 系统有许多独立设计子组件工程
  • 大量特征工程
    • 很多功能需要设计特性来获取特定的语言现象
  • 需要编译和维护额外的资源
    • 比如双语短语对应表
  • 需要大量的人力来维护
    • 对于每一对语言都需要重复操作

2.神经网络机器翻译

2.1 Neural Machine Translation

2.2 神经机器翻译(NMT)

2.3 神经机器翻译(NMT)

• 神经机器翻译(NMT)是利用单个神经网络进行机器翻译的一种方法

• 神经网络架构称为 sequence-to-sequence (又名seq2seq)，它包含两个RNNs

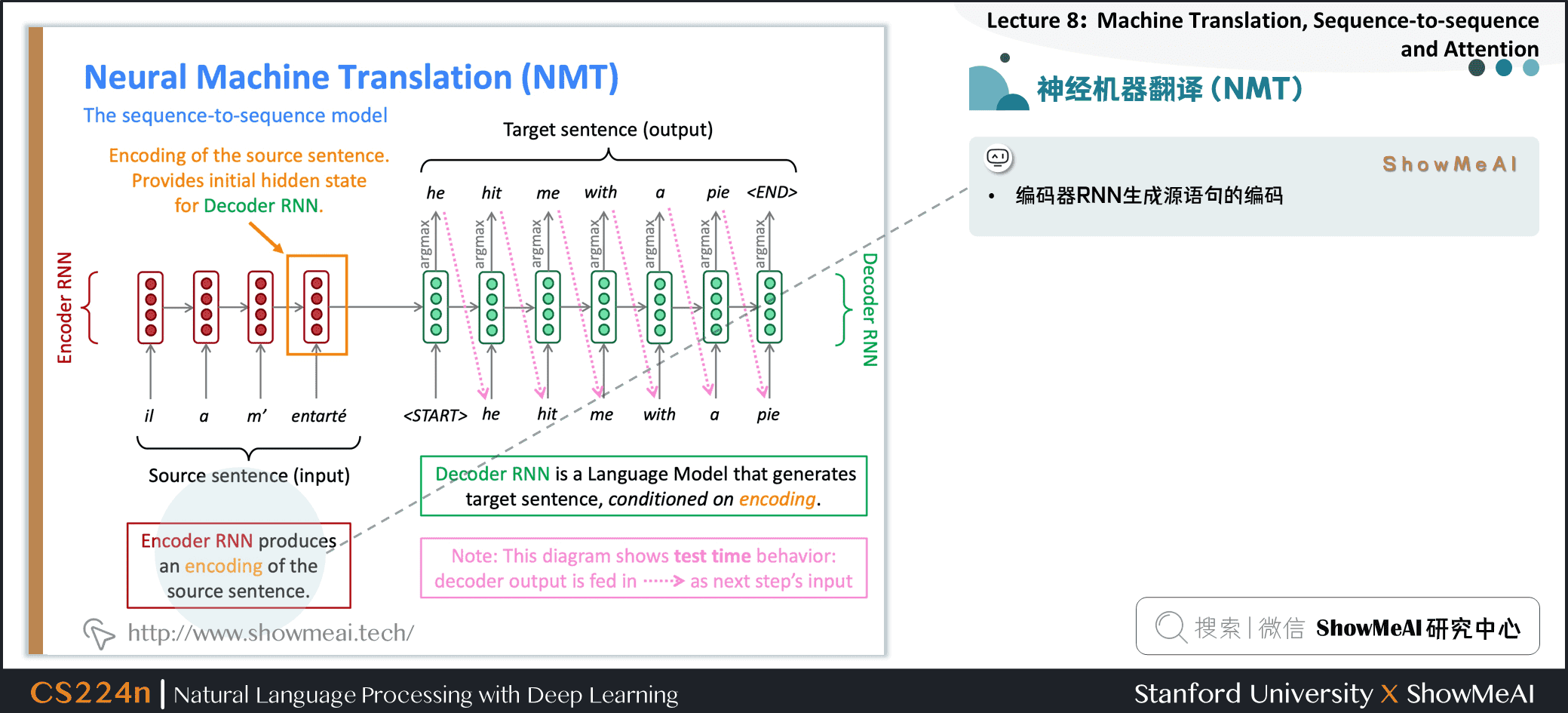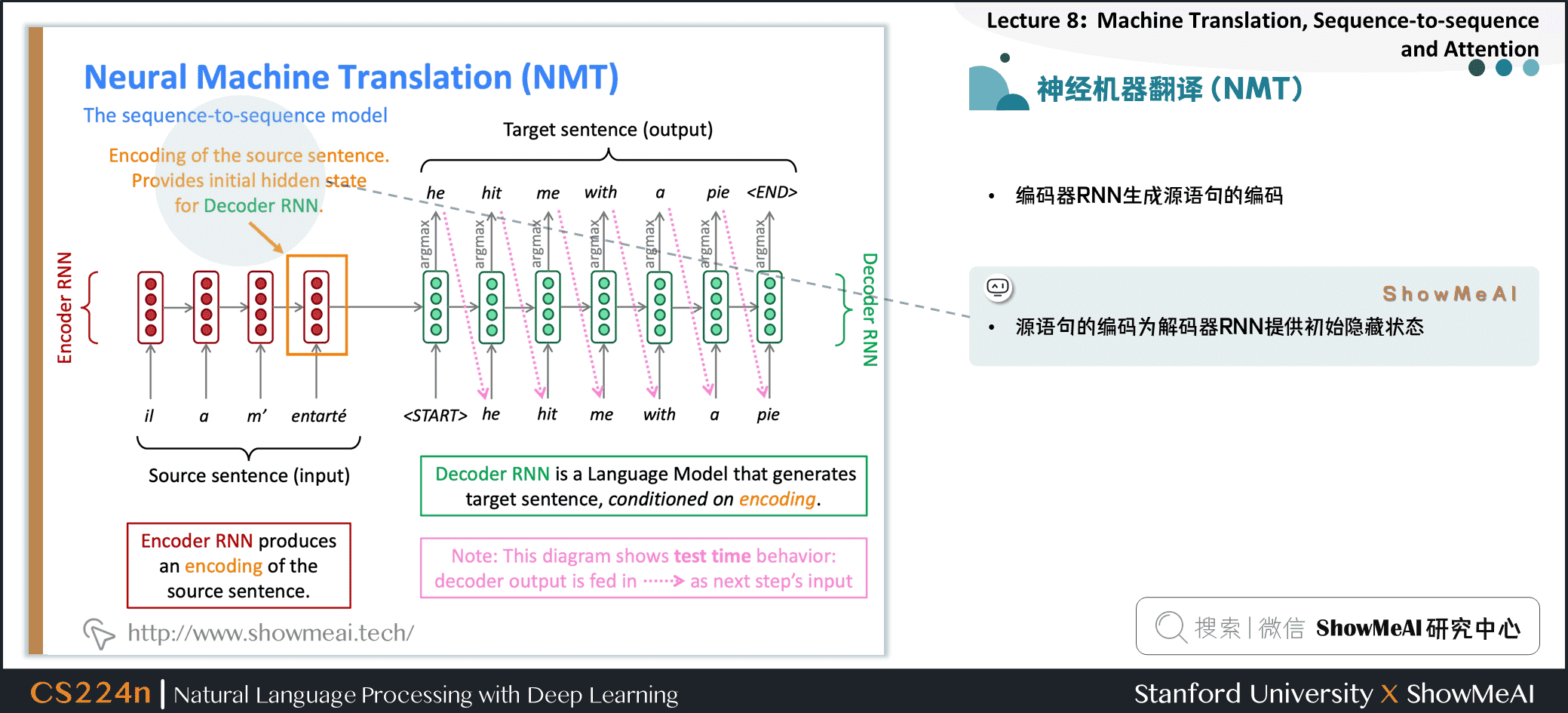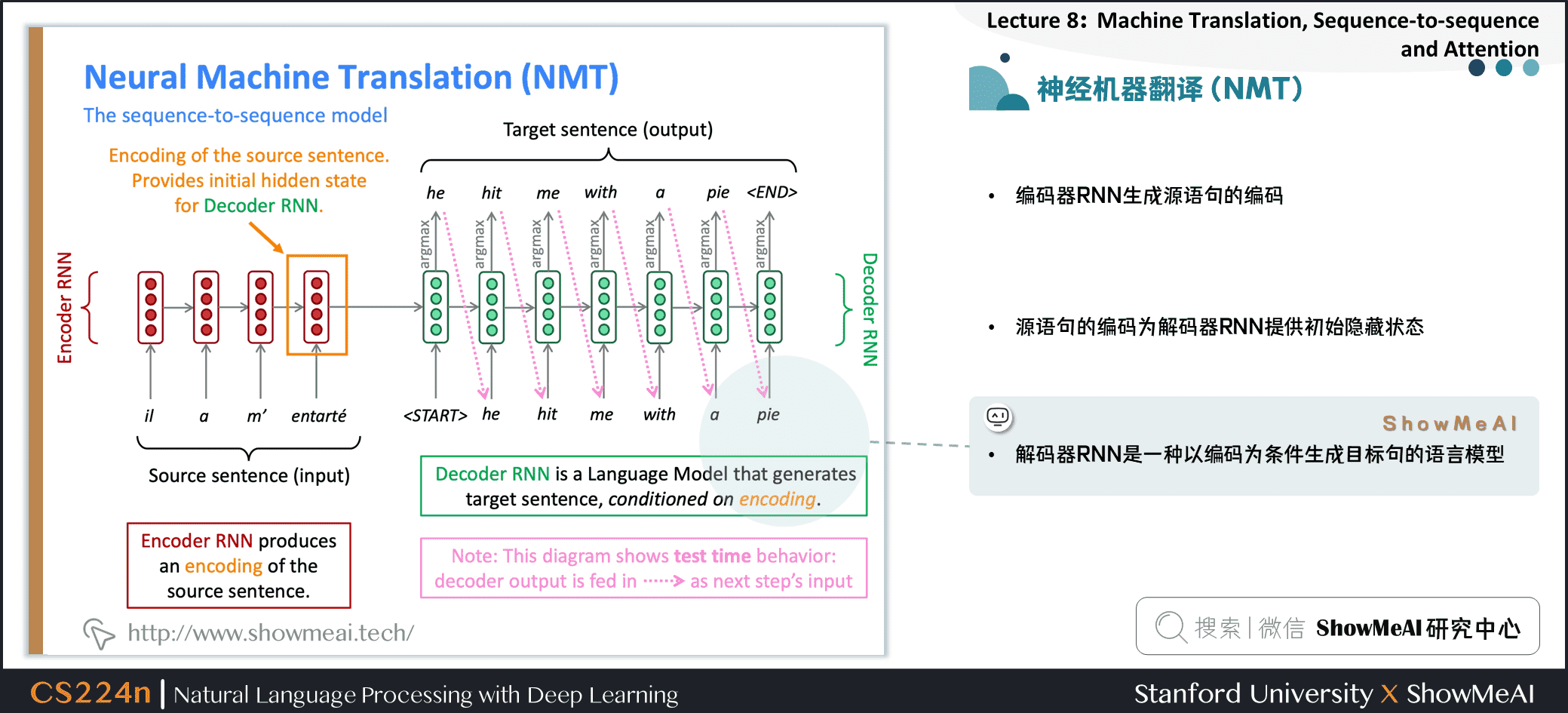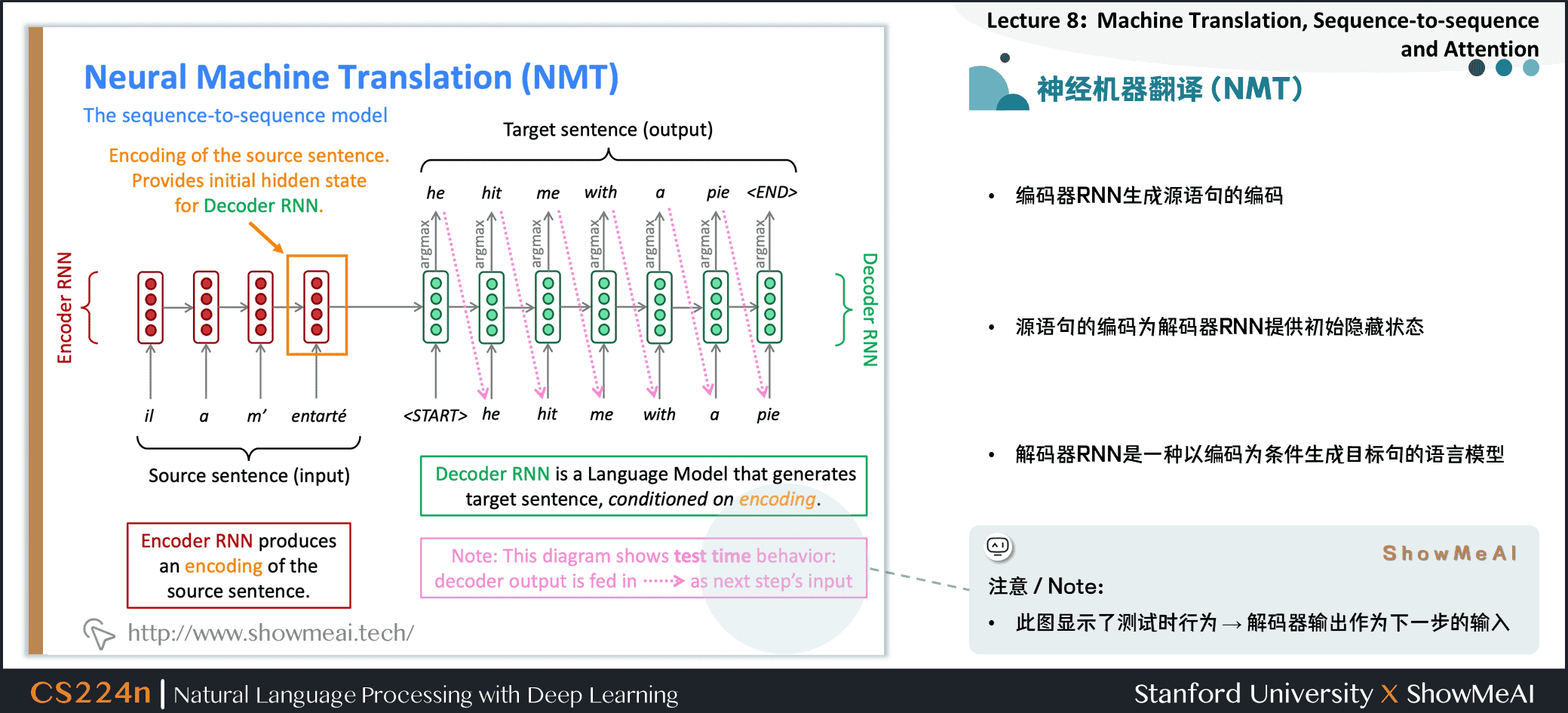
2.4 神经机器翻译(NMT)

• 编码器RNN生成源语句的编码

• 源语句的编码为解码器RNN提供初始隐藏状态

• 解码器RNN是一种以编码为条件生成目标句的语言模型

• 注意：此图显示了测试时行为 → 解码器输出作为下一步的输入

2.5 Sequence-to-sequence是多功能的！

• 序列到序列不仅仅对机器翻译有用

• 许多NLP任务可以按照顺序进行表达

  • 摘要(长文本 → 短文本)
  • 对话(前一句话 → 下一句话)
  • 解析(输入文本 → 输出解析为序列)
  • 代码生成(自然语言 → Python代码)

2.6 神经机器翻译(NMT)

• sequence-to-sequence 模型是条件语言模型的一个例子

  • 语言模型(Language Model)，因为解码器正在预测目标句的下一个单词 $y$
  • 条件约束的(Conditional)，因为预测也取决于源句 $x$

• NMT直接计算 $P(y\mid x)$

$$P(y|x)=P\left(y_1|x\right)P\left(y_2|y_1,x\right)P\left(y_3|y_1,y_2,x\right)\dots P\left(y_T|y_1,\dots ,y_{T-1},x\right)$$

• 上式中最后一项为，给定到目前为止的目标词和源句 $x$，下一个目标词的概率

• 问题：如何训练NMT系统？

• 回答：找一个大的平行语料库

2.7 训练一个机器翻译系统

• Seq2seq被优化为一个单一的系统。反向传播运行在“端到端”中

3.机器翻译解码

3.1 贪婪解码

• 我们了解了如何生成(或“解码”)目标句，通过对解码器的每个步骤使用 argmax

• 这是贪婪解码(每一步都取最可能的单词)

• 这种方法有问题吗？

3.2 贪婪解码的问题

• 贪婪解码没有办法撤销决定

• 如何修复？

3.3 穷举搜索解码

• 理想情况下，我们想要找到一个(长度为 $T$ )的翻译 $y$ 使其最大化

• 我们可以尝试计算所有可能的序列 $y$

  • 这意味着在解码器的每一步 $t$ ，我们跟踪 $V^t$个可能的部分翻译，其中 $V$ 是 vocab 大小
  • 这种 $O(V^T)$ 的复杂性太昂贵了！

3.4 集束搜索解码

• 核心思想：在解码器的每一步，跟踪 $k$ 个最可能的部分翻译(我们称之为假设[hypotheses ] )

  • $k$ 是Beam的大小(实际中大约是5到10)

• 假设 $y_1,\dots ,y_t$ 有一个分数，即它的对数概率

$$\mathrm{score}\left(y_1,\dots ,y_t\right)=\log P_{\mathrm{L}\mathrm{M}}\left(y_1,\dots ,y_t|x\right)=\sum _{i=1}^t\log P_{\mathrm{LM}}\left(y_i|y_1,\dots ,y_{i-1},x\right)$$

• 分数都是负数，分数越高越好

• 我们寻找得分较高的假设，跟踪每一步的 top k 个部分翻译

• 波束搜索 不一定能 找到最优解

• 但比穷举搜索效率高得多

3.5 集束搜索解码：示例

• Beam size = k = 2
• 蓝色的数字是

$$\mathrm{score}\left(y_1,\dots ,y_t\right)=\sum _{i=1}^t\log P_{\mathrm{LM}}\left(y_i|y_1,\dots ,y_{i-1},x\right)$$

• 计算下一个单词的概率分布
• 取前 $k$ 个单词并计算分数
  • 对于每一次的 $k$ 个假设，找出最前面的 $k$ 个单词并计算分数
  • 在 $k^2$ 的假设中，保留 $k$ 个最高的分值
    • $t=2$ 时，保留分数最高的 hit 和 was
    • $t=3$ 时，保留分数最高的 a 和 me
    • $t=4$ 时，保留分数最高的 pie 和 with
    • $t=5$ 时，保留分数最高的 a 和 one
    • $t=6$ 时，保留分数最高的 pie
• 这是最高得分的假设
• 回溯以获得完整的假设

3.6 集束搜索解码：停止判据

• 在贪心解码中，我们通常解码到模型产生一个 令牌

  • 例如： he hit me with a pie

• 在集束搜索解码中，不同的假设可能在不同的时间步长上产生 令牌

  • 当一个假设生成了 令牌，该假设完成
  • 把它放在一边，通过 Beam Search 继续探索其他假设

• 通常我们继续进行 Beam Search ，直到

  • 我们到达时间步长 $T$ (其中 $T$ 是预定义截止点)
  • 我们至少有 $n$ 个已完成的假设(其中 $n$ 是预定义截止点)

3.7 集束搜索解码：完成

• 我们有完整的假设列表

• 如何选择得分最高的？

• 我们清单上的每个假设 $y_1,\dots ,y_t$ 都有一个分数

$$\mathrm{score}\left(y_1,\dots ,y_t\right)=\log P_{\mathrm{L}\mathrm{M}}\left(y_1,\dots ,y_t\mid x\right)=\sum _{i=1}^t\log P_{\mathrm{LM}}\left(y_i\mid y_1,\dots ,y_{i-1},x\right)$$

• 问题在于 ：较长的假设得分较低

• 修正：按长度标准化。用下式来选择top one

$$\frac{1}{t}\sum _{i=1}^t\log P_{\mathrm{L}\mathrm{M}}\left(y_i\mid y_1,\dots ,y_{i-1},x\right)$$

3.8 神经机器翻译(NMT)的优点

与SMT相比，NMT有很多优点

• 更好的性能

  • 更流利
  • 更好地使用上下文
  • 更好地使用短语相似性

• 单个神经网络端到端优化

  • 没有子组件需要单独优化

• 需要更少的人类工程付出

  • 无特征工程
  • 所有语言对的方法相同

3.9 神经机器翻译(NMT)的缺点

SMT相比，NMT的缺点

• NMT的可解释性较差

  • 难以调试

• NMT很难控制

  • 例如，不能轻松指定翻译规则或指南
  • 安全问题

4.机器翻译评估

4.1 如何评估机器翻译质量

• BLEU (Bilingual Evaluation Understudy)

  • 你将会在 Assignment 4 中看到BLEU的细节

• BLEU将机器翻译和人工翻译(一个或多个)，并计算一个相似的分数

  • n-gram 精度 (n通常为1-4)
  • 对过于短的机器翻译的加上惩罚

• BLEU很有用，但不完美

  • 有很多有效的方法来翻译一个句子
  • 所以一个好的翻译可以得到一个糟糕的BLEU score，因为它与人工翻译的n-gram重叠较低

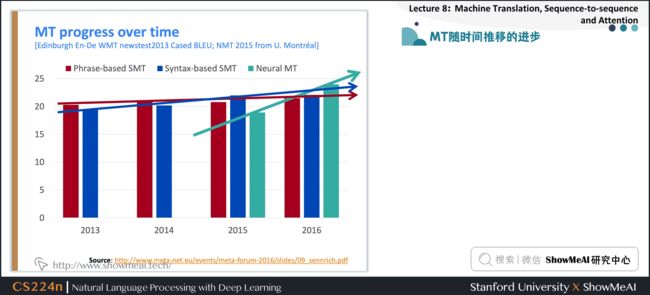
4.2 MT随时间推移的进步

Source: http://www.meta-net.eu/events/meta-forum-2016/slides/09_sennrich.pdf

4.3 NMT：NLP深度学习的最大成功案例

神经机器翻译于2014年从边缘研究活动到2016年成为领先标准方法

• 2014：第一篇 seq2seq 的文章发布

• 2016：谷歌翻译从 SMT 换成了 NMT

• 这是惊人的

  • 由数百名工程师历经多年打造的SMT系统，在短短几个月内就被少数工程师训练过的NMT系统超越

4.4 机器翻译问题完美解决了吗？

Further reading: “Has AI surpassed humans at translation? Not even close!” https://www.skynettoday.com/editorials/state_of_nmt

Source: https://hackernoon.com/bias-sexist-or-this-is-the-way-it-should-be-ce1f7c8c683c

Picture source: https://www.vice.com/en_uk/article/j5npeg/why-is-google-translate-spitting-out-sinister-religious-prophecies

Explanation: https://www.skynettoday.com/briefs/google-nmt-prophecies

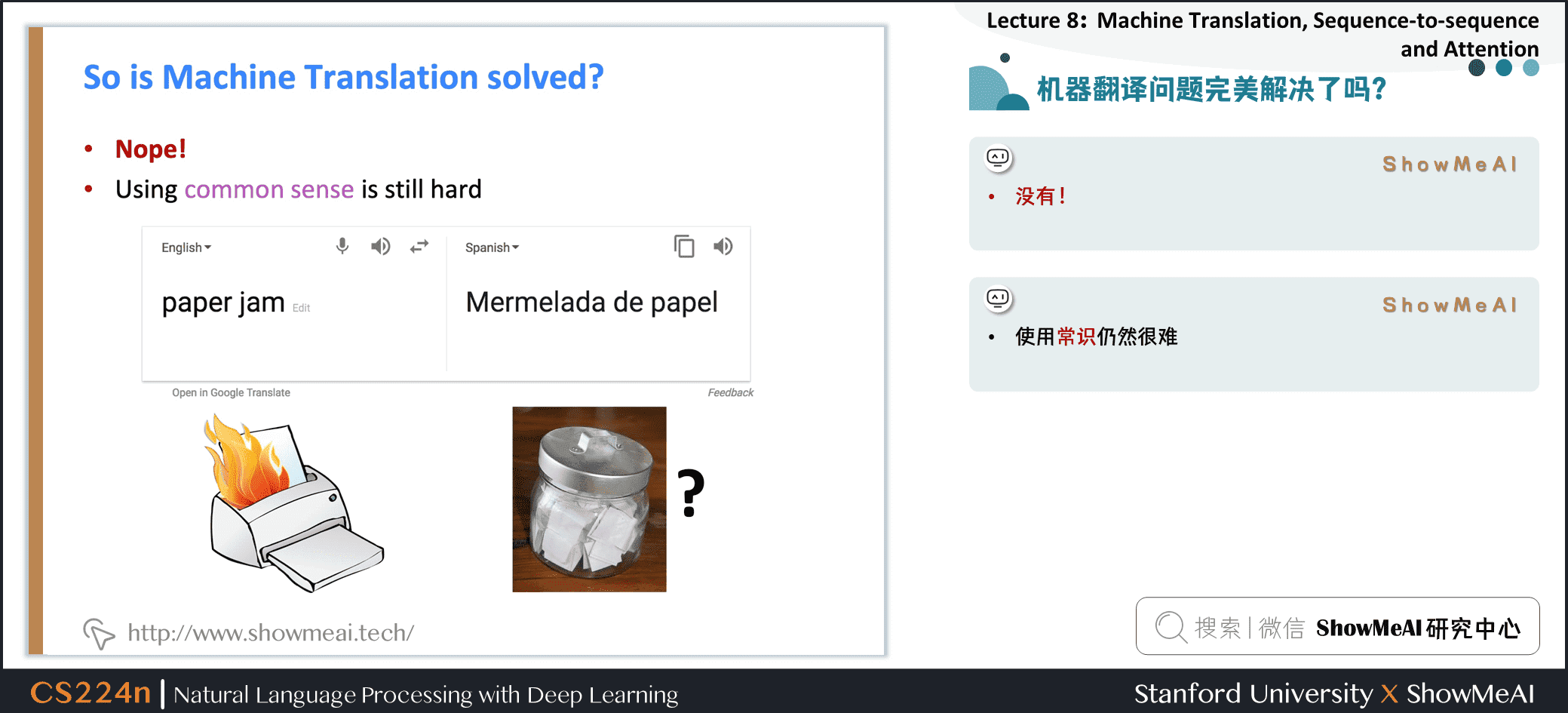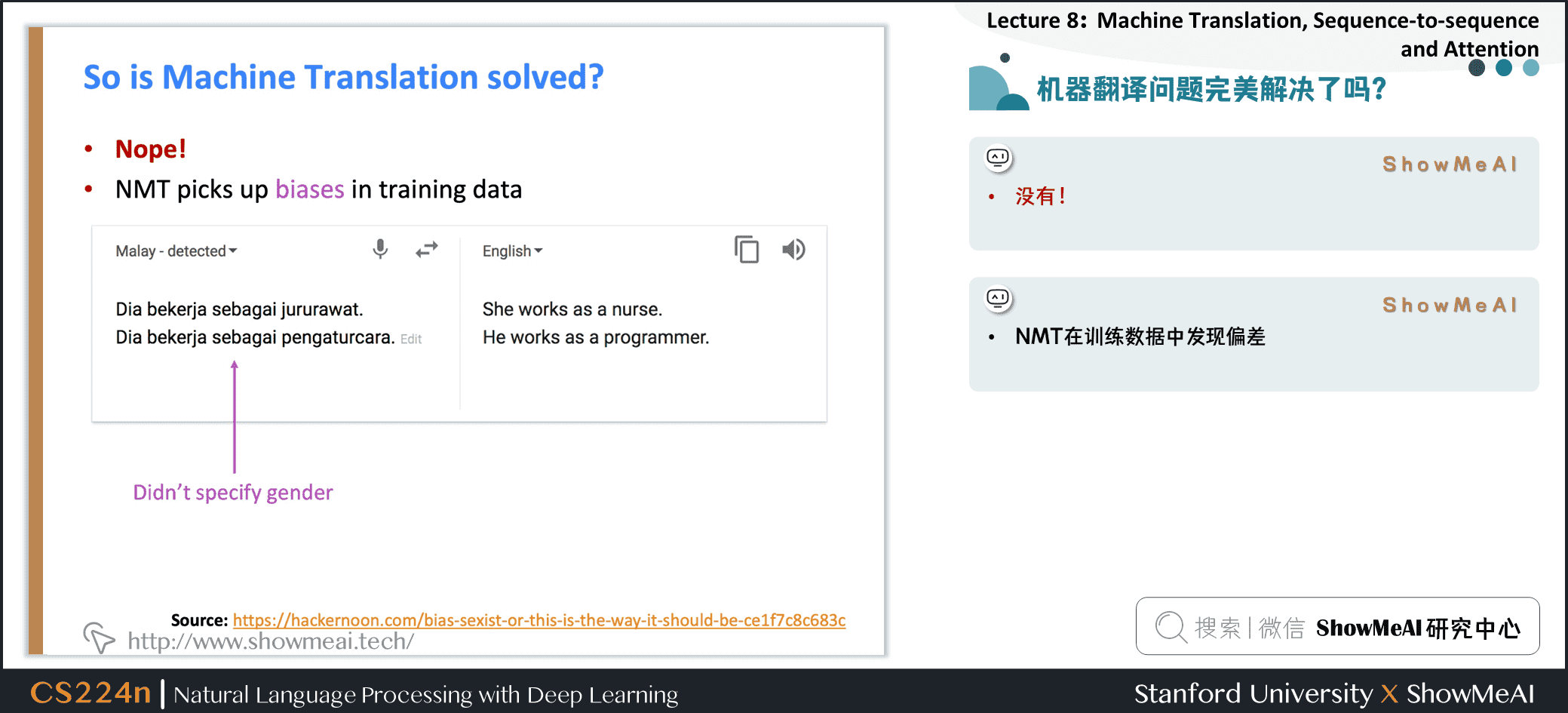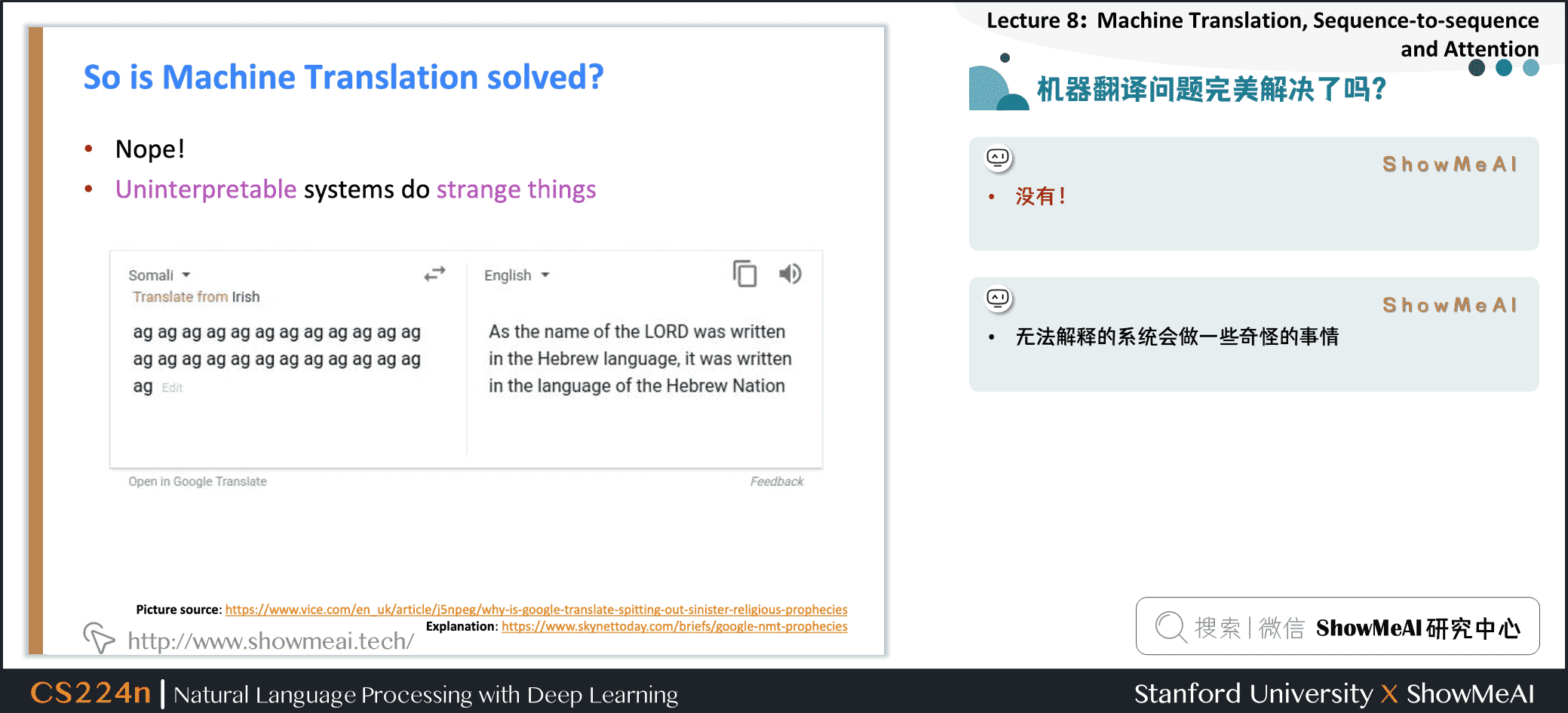
• 没有！

• 许多困难仍然存在

  • 词表外的单词处理
  • 训练和测试数据之间的领域不匹配
  • 在较长文本上维护上下文
  • 资源较低的语言对

• 使用常识仍然很难

• NMT在训练数据中发现偏差

• 无法解释的系统会做一些奇怪的事情

4.5 NMT研究仍在继续

• NMT是NLP深度学习的核心任务

• NMT研究引领了NLP深度学习的许多最新创新

• 2019年：NMT研究将继续蓬勃发展

  • 研究人员发现，对于我们今天介绍的普通seq2seq NMT系统，有很多、很多的改进。
  • 但有一个改进是如此不可或缺

5.注意力机制

5.1 Attention

5.2 Sequence-to-sequence：瓶颈问题

• 源语句的编码
• 需要捕获关于源语句的所有信息
• 信息瓶颈！

5.3 注意力

• 注意力为瓶颈问题提供了一个解决方案

• 核心理念：在解码器的每一步，使用与编码器的直接连接来专注于源序列的特定部分

• 首先我们将通过图表展示(没有方程)，然后我们将用方程展示

5.4 带注意力机制的序列到序列模型

• 将解码器部分的第一个token 与源语句中的每一个时间步的隐藏状态进行 Dot Product 得到每一时间步的分数

• 通过softmax将分数转化为概率分布

• 在这个解码器时间步长上，我们主要关注第一个编码器隐藏状态(“he”)

• 利用注意力分布对编码器的隐藏状态进行加权求和

• 注意力输出主要包含来自于受到高度关注的隐藏状态的信息

• 连接的注意力输出与解码器隐藏状态 ，然后用来计算 ${\hat{y}}_1$

• 有时，我们从前面的步骤中提取注意力输出，并将其输入解码器(连同通常的解码器输入)。我们在作业4中做这个。

5.5 注意力：公式

• 我们有编码器隐藏状态 $h_1,\dots ,h_N\in {\mathbb{R}}^h$
• 在时间步 $t$ 上，我们有解码器隐藏状态 $s_t\in {\mathbb{R}}^h$
• 我们得到这一步的注意分数

$$e^t=\left[s_t^T{\mathbf{h}}_1,\dots ,{\mathbf{s}}_t^T{\mathbf{h}}_N\right]\in {\mathbb{R}}^N$$

• 我们使用softmax得到这一步的注意分布 ${\alpha }^t$ (这是一个概率分布，和为1)

$${\alpha }^t=\mathrm{softmax}\left(e^t\right)\in {\mathbb{R}}^N$$

• 我们使用 ${\alpha }^t$ 来获得编码器隐藏状态的加权和，得到注意力输出 ${\alpha }^t$

$${\mathbf{a}}_t=\sum _{i=1}^N{\alpha }_i^t{\mathbf{h}}_i\in {\mathbb{R}}^h$$

• 最后，我们将注意输出 ${\alpha }^t$ 与解码器隐藏状态连接起来，并按照非注意 seq2seq 模型继续进行

$$\left[{\mathbf{a}}_t;{\mathbf{s}}_t\right]\in {\mathbb{R}}^{2h}$$

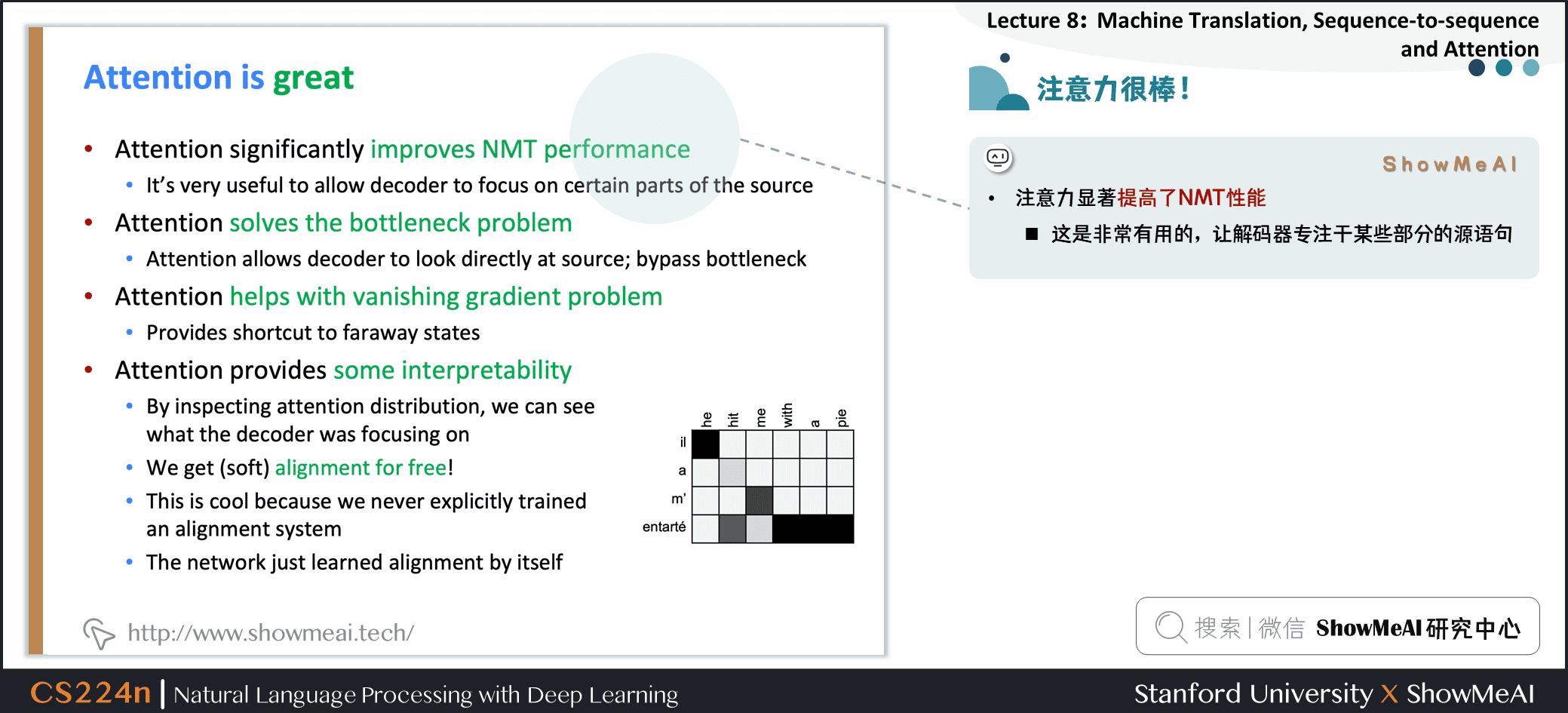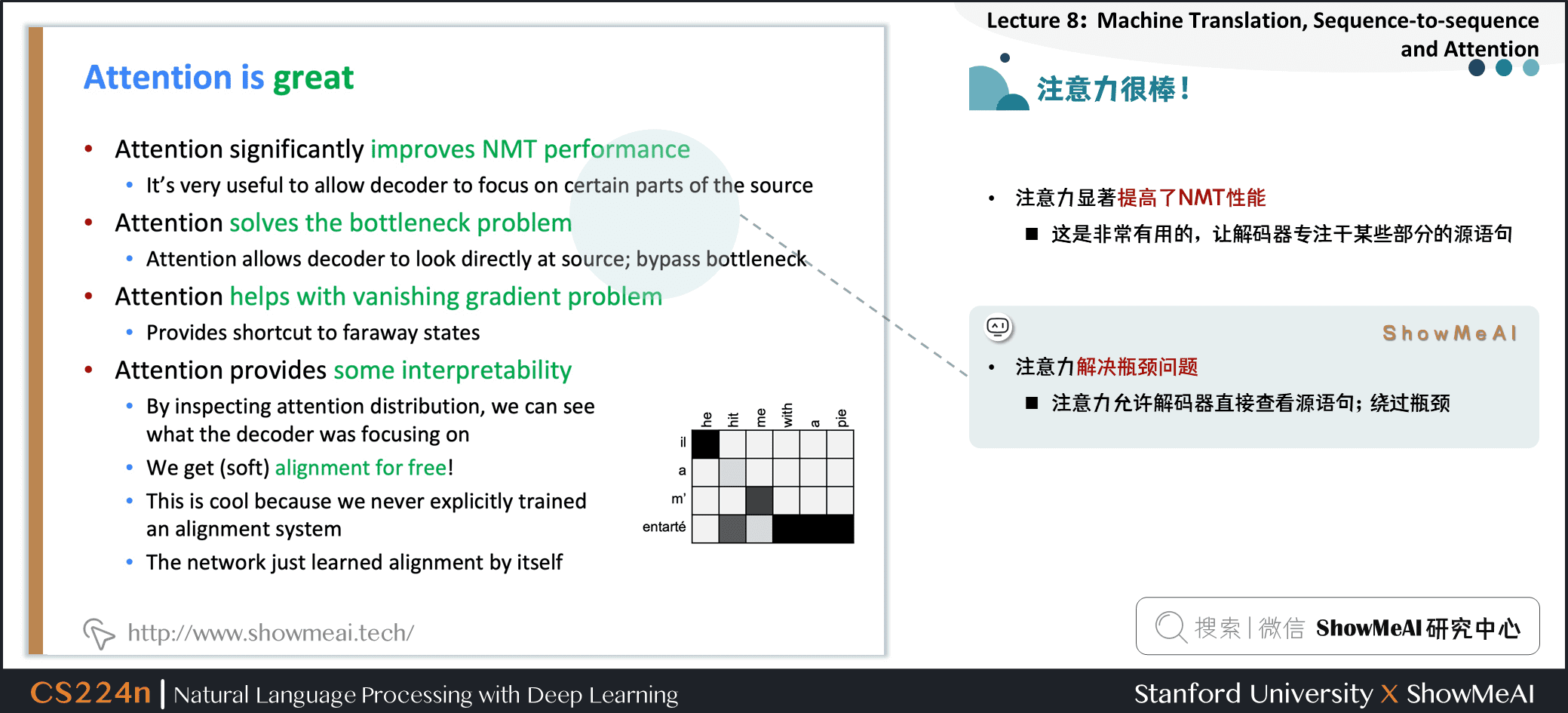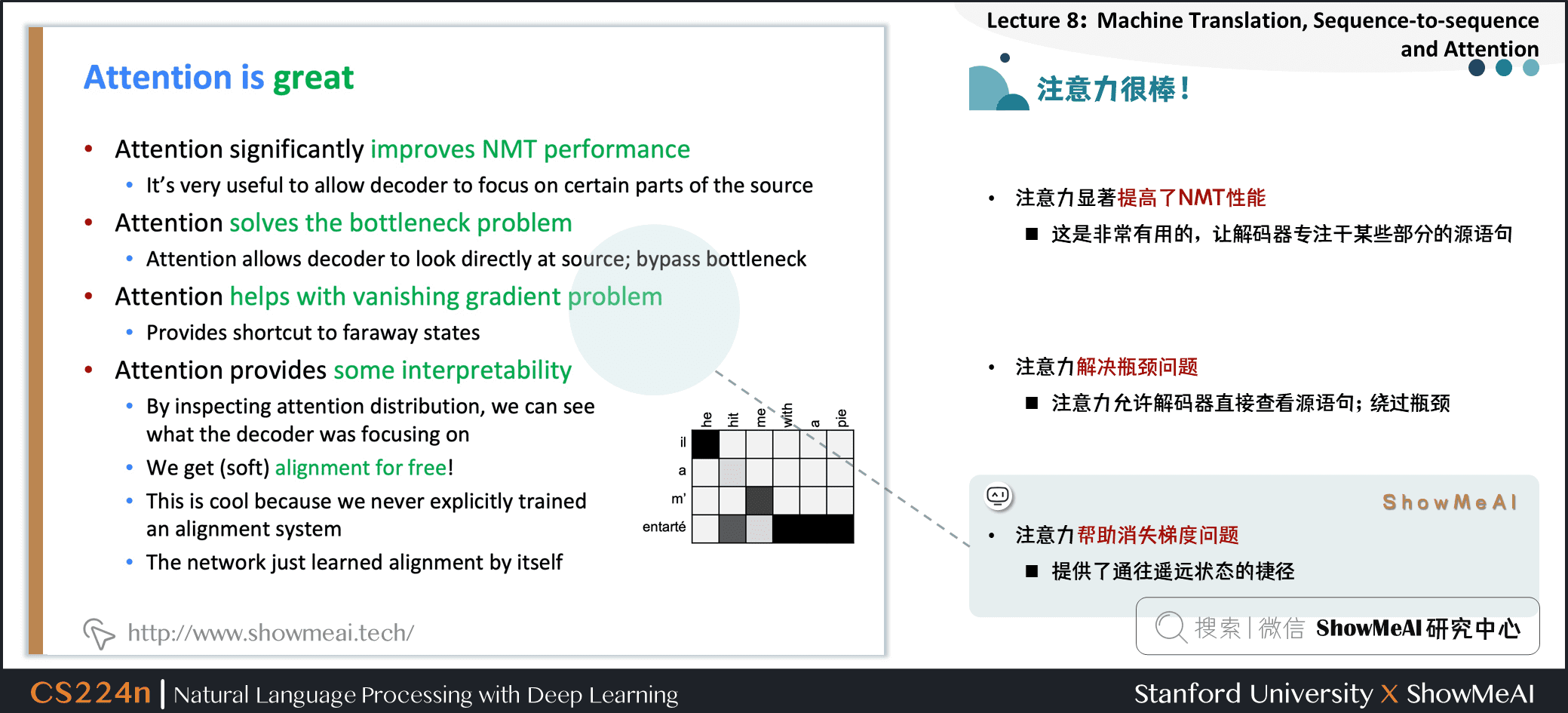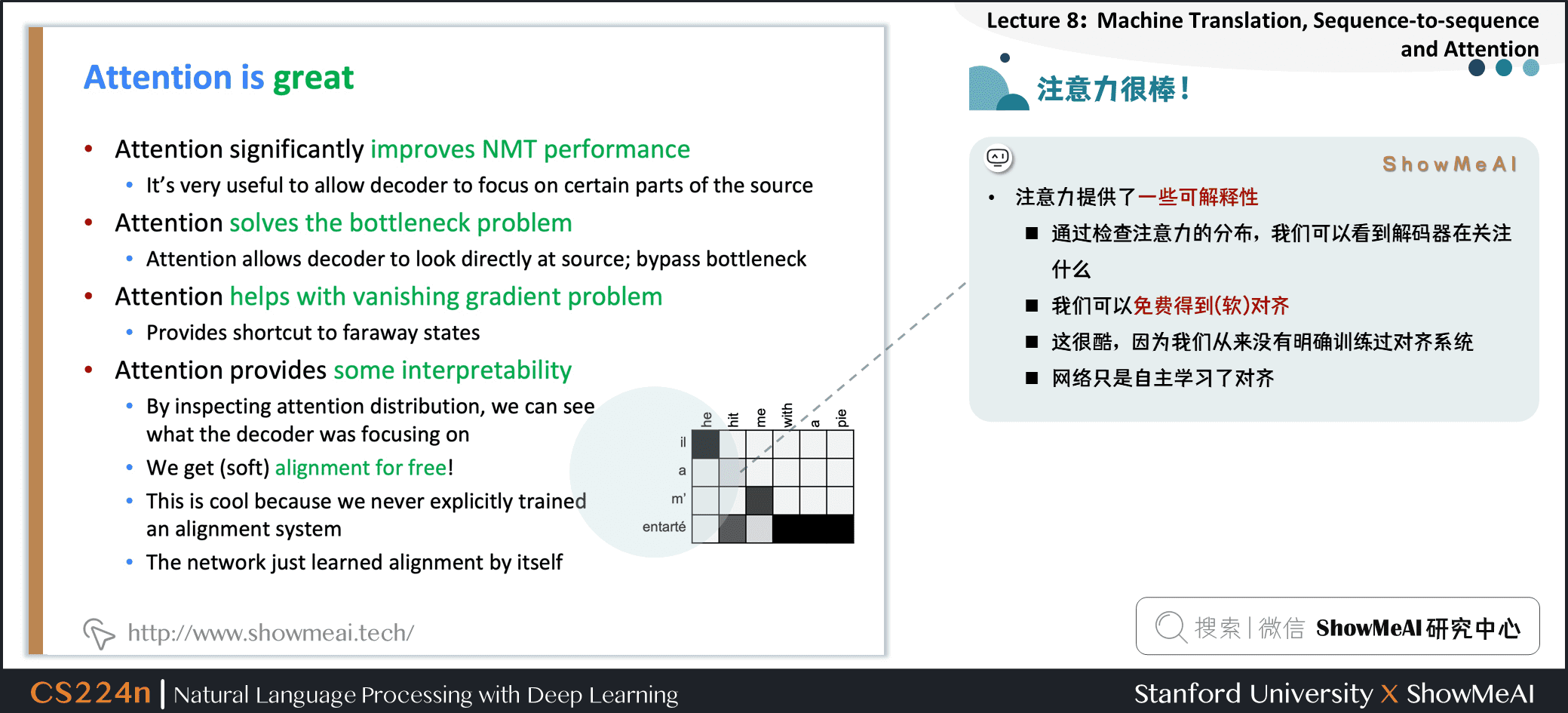
5.6 注意力很棒！

• 注意力显著提高了NMT性能

  • 这是非常有用的，让解码器专注于某些部分的源语句

• 注意力解决瓶颈问题

  • 注意力允许解码器直接查看源语句；绕过瓶颈

• 注意力帮助消失梯度问题

  • 提供了通往遥远状态的捷径

• 注意力提供了一些可解释性

  • 通过检查注意力的分布，我们可以看到解码器在关注什么
  • 我们可以免费得到(软)对齐
  • 这很酷，因为我们从来没有明确训练过对齐系统
  • 网络只是自主学习了对齐

5.7 注意力是一种普遍的深度学习技巧

• 我们已经看到，注意力是改进机器翻译的序列到序列模型的一个很好的方法

• 然而：你可以在许多结构(不仅仅是seq2seq)和许多任务(不仅仅是MT)中使用注意力

• 我们有时说 query attends to the values

• 例如，在seq2seq + attention模型中，每个解码器的隐藏状态(查询)关注所有编码器的隐藏状态(值)

5.8 注意力是一种普遍的深度学习技巧

• 注意力的更一般定义

  • 给定一组向量值和一个向量查询，注意力是一种根据查询，计算值的加权和的技术

• 直觉

  • 加权和是值中包含的信息的选择性汇总，查询在其中确定要关注哪些值
  • 注意是一种获取任意一组表示(值)的固定大小表示的方法，依赖于其他一些表示(查询)。

5.9 有几种注意力的变体

• 候选值 ${\mathbf{h}}_1,\dots ,{\mathbf{h}}_N\in {\mathbb{R}}^{d_1}$，查询 $s\in {\mathbb{R}}^{d_2}$

• 注意力总是包括：

  • 计算注意力得分 $e\in {\mathbb{R}}^N$ (很多种计算方式)
  • 采取softmax来获得注意力分布 $\alpha$

$$\alpha =\mathrm{softmax}(\mathbf{e})\in {\mathbb{R}}^N$$

• 使用注意力分布对值进行加权求和：从而得到注意力输出 $\alpha$ (有时称为上下文向量)

$$\mathbf{a}=\sum _{i=1}^N{\alpha }_i{\mathbf{h}}_i\in {\mathbb{R}}^{d_1}$$

5.10 注意力的变体

More information: “Deep Learning for NLP Best Practices”, Ruder, 2017. http://ruder.io/deep-learning-nlp-best-practices/index.html#attention
“Massive Exploration of Neural Machine Translation Architectures”, Britz et al, 2017, https://arxiv.org/pdf/1703.03906.pdf

• 有几种方法可以从 ${\mathbf{h}}_1,\dots ,{\mathbf{h}}_N\in {\mathbb{R}}^{d_1}$ 计算 $e\in {\mathbb{R}}^N$ 和 $s\in {\mathbb{R}}^{d_2}$

• 基本的点乘注意力 ${\mathbf{e}}_i={\mathbf{s}}^T{\mathbf{h}}_i\in \mathbb{R}$

  • 注意：这里假设 $d_1=d_2$ [这是我们之前看到的版本]

• 乘法注意力 $e_i=s^T\mathbf{W}{\mathbf{h}}_i\in \mathbb{R}$

  • $\mathbf{W}\in {\mathbb{R}}^{d_2\times d_1}$ 是权重矩阵

• 加法注意力 $e_i={\mathbf{v}}^T\tanh \left({\mathbf{W}}_1{\mathbf{h}}_i+{\mathbf{W}}_2\mathbf{s}\right)\in \mathbb{R}$

  • 其中 ${\mathbf{W}}_1\in {\mathbb{R}}^{d_3\times d_1},{\mathbf{W}}_2\in {\mathbb{R}}^{d_3\times d_2}$ 是权重矩阵，$\mathbf{v}\in {\mathbb{R}}^{d_3}$ 是权重向量 ，$d_3$ (注意力维度)是一个超参数

5.11 课程总结

• 我们学习了一些机器翻译的历史

• 自2014年以来，神经机器翻译迅速取代了复杂的统计机器翻译

• Sequence-to-sequence 是NMT的体系结构(使用2个RNN)

• 注意力是一种集中注意力的方法

  • 从序列到序列改进了很多

6.视频教程

可以点击 B站 查看视频的【双语字幕】版本

【双语字幕+资料下载】斯坦福CS224n | 深度学习与自然语言处理(2019·全20讲)

7.参考资料

• 《斯坦福NLP名课带学详解 | CS224n》本讲带学的动态翻页PPT在线阅翻页-Lecture8
• 《斯坦福CS224n深度学习与自然语言处理》课程学习指南
• 《斯坦福CS224n深度学习与自然语言处理》课程大作业解析
• 【双语字幕视频】斯坦福CS224n | 深度学习与自然语言处理(2019·全20讲)
• Stanford官网 | CS224n: Natural Language Processing with Deep Learning

ShowMeAI 深度学习与自然语言处理教程（完整版）

• ShowMeAI 深度学习与自然语言处理教程(1) - 词向量、SVD分解与Word2vec
• ShowMeAI 深度学习与自然语言处理教程(2) - GloVe及词向量的训练与评估
• ShowMeAI 深度学习与自然语言处理教程(3) - 神经网络与反向传播
• ShowMeAI 深度学习与自然语言处理教程(4) - 句法分析与依存解析
• ShowMeAI 深度学习与自然语言处理教程(5) - 语言模型、RNN、GRU与LSTM
• ShowMeAI 深度学习与自然语言处理教程(6) - 神经机器翻译、seq2seq与注意力机制
• ShowMeAI 深度学习与自然语言处理教程(7) - 问答系统
• ShowMeAI 深度学习与自然语言处理教程(8) - NLP中的卷积神经网络
• ShowMeAI 深度学习与自然语言处理教程(9) - 句法分析与树形递归神经网络

ShowMeAI 斯坦福NLP名课 CS224n带学详解（20讲·完整版）

• 斯坦福NLP名课带学详解 | CS224n 第1讲 - NLP介绍与词向量初步
• 斯坦福NLP名课带学详解 | CS224n 第2讲 - 词向量进阶
• 斯坦福NLP名课带学详解 | CS224n 第3讲 - 神经网络知识回顾
• 斯坦福NLP名课带学详解 | CS224n 第4讲 - 神经网络反向传播与计算图
• 斯坦福NLP名课带学详解 | CS224n 第5讲 - 句法分析与依存解析
• 斯坦福NLP名课带学详解 | CS224n 第6讲 - 循环神经网络与语言模型
• 斯坦福NLP名课带学详解 | CS224n 第7讲 - 梯度消失问题与RNN变种
• 斯坦福NLP名课带学详解 | CS224n 第8讲 - 机器翻译、seq2seq与注意力机制
• 斯坦福NLP名课带学详解 | CS224n 第9讲 - cs224n课程大项目实用技巧与经验
• 斯坦福NLP名课带学详解 | CS224n 第10讲 - NLP中的问答系统
• 斯坦福NLP名课带学详解 | CS224n 第11讲 - NLP中的卷积神经网络
• 斯坦福NLP名课带学详解 | CS224n 第12讲 - 子词模型
• 斯坦福NLP名课带学详解 | CS224n 第13讲 - 基于上下文的表征与NLP预训练模型
• 斯坦福NLP名课带学详解 | CS224n 第14讲 - Transformers自注意力与生成模型
• 斯坦福NLP名课带学详解 | CS224n 第15讲 - NLP文本生成任务
• 斯坦福NLP名课带学详解 | CS224n 第16讲 - 指代消解问题与神经网络方法
• 斯坦福NLP名课带学详解 | CS224n 第17讲 - 多任务学习(以问答系统为例)
• 斯坦福NLP名课带学详解 | CS224n 第18讲 - 句法分析与树形递归神经网络
• 斯坦福NLP名课带学详解 | CS224n 第19讲 - AI安全偏见与公平
• 斯坦福NLP名课带学详解 | CS224n 第20讲 - NLP与深度学习的未来

ShowMeAI系列教程精选推荐

• 大厂技术实现：推荐与广告计算解决方案
• 大厂技术实现：计算机视觉解决方案
• 大厂技术实现：自然语言处理行业解决方案
• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解大数据技术：从入门到精通系列教程
• 图解机器学习算法：从入门到精通系列教程
• 机器学习实战：手把手教你玩转机器学习系列
• 深度学习教程：吴恩达专项课程 · 全套笔记解读
• 自然语言处理教程：斯坦福CS224n课程 · 课程带学与全套笔记解读
• 深度学习与计算机视觉教程：斯坦福CS231n · 全套笔记解读