MATLB|具有储能的经济调度及机会约束和鲁棒优化

欢迎来到本博客❤️❤️❤️

作者研究：本科计算机专业，研究生电气学硕。主要研究方向是电力系统和智能算法、机器学习和深度学习。目前熟悉python网页爬虫、机器学习、群智能算法、深度学习的相关内容。希望将计算机和电网有效结合！⭐️⭐️⭐️
博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者，博主专门做了一个专栏目录，整个专栏只放了一篇文章，足见我对其重视程度：博主专栏目录。做到极度细致，方便大家进行学习！亲民！！！还有我开了一个专栏给女朋友的，很浪漫的喔，代码学累的时候去瞧一瞧，看一看：女朋友的浪漫邂逅。有问题可以私密博主，博主看到会在第一时间回复。
目前更新：电力系统相关知识，期刊论文，算法，机器学习和人工智能学习。
支持：如果觉得博主的文章还不错或者您用得到的话，可以免费的关注一下博主，如果三连收藏支持就更好啦！这就是给予我最大的支持！

                          

                                    欢迎您的到来

                     ⛅⛅⛅ 博主主页：电力系统科研室

                    专栏目录：电力系统与算法之美‍‍‍

                       

                          

‍博主课外兴趣：中西方哲学，送予读者：

‍做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。在我这个专栏记录我有空时的一些哲学思考和科研笔记：科研和哲思。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“真理”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......

本文目录如下：⛳️⛳️⛳️：

1 概述

2 机会约束方法

3 算例及Matlab代码实现

3.1 算例

3.2 Matlab代码

3.3 结果 

4 写在最后 

 1 概述

IT 是一个普遍的信念，即全球变暖正在推进。因此，必须采取紧急有效的碳减排政策，即碳税、总量控制和交易等。新的理论上，这些政策可以减少对碳密集型能源的依赖，鼓励可再生能源，从而纠正负面的环境外部性。但在实践中，现行的碳减排政策可能会提高区域电价，造成效率低下、分配不公平等经济问题。因此，它们并未得到普遍实施。然而，新冠病毒危机爆发后，在实践中实施此类政策的机会已经出现。尽管冠状病毒危机导致制造业停滞，但它也减缓了全球变暖的趋势，因为在能源部门，2020 年第一季度的碳排放量同比减少了 3.8% 。一方面，低碳排放水平使得与减碳政策相关的成本在实施时较低。为了在恢复正常生产的情况下保持这种成本水平，这个停滞期是碳密集型行业为自身经济利益进行改造的绝佳时期。另一方面，这种改造可以增加就业，从而解决他们的社会问题。因此，迫切需要利用这一宝贵时期，增强减碳政策的实用性。

在电力部门，碳税是一项旨在减少二氧化碳排放的常见环境政策，但通常被认为在经济上不友好，特别是对于依赖燃煤和其他碳密集型发电机的地区。利用储能系统的电网可能是缓解实施碳税的电网区域经济压力的有前景的解决方案。随着清洁能源（例如太阳能和风能）的日益开发，在这项工作中，我们使用两个框架（即机会约束框架和鲁棒优化框架）来描述具有存储系统的随机排放感知经济调度。我们通过研究稳健性和总体成本之间的权衡来突出它们的差异和联系。具体来说，我们将这两个框架与一个新颖的分布式鲁棒优化框架联系起来，该框架考虑实际边界来估计可靠性要求下的最佳系统性能。对IEEE-6节点模型和 IEEE-118 节点的数值研究进一步证明。

2 机会约束方法

能够处理不确定性的两种最广泛使用的优化方法是随机优化 (SO)，其中包括 CC 方法和 RO 方法。传统的 SO 方法通常是基于场景的。为了

CC方法由 Charnes 中提出。使用 CC 方法的动机是避免过度的系统冗余，这表明某些约束可以在有限的时间内被违反。不确定性下的优化问题通常采用以下形式：

                  

其中是目标函数；u是状态变量的向量（例如SOC、）；x是决策变量的向量（例如，每个发电机的功率输出）；ζ是随机变量的向量（例如，可再生输出）。等式（2 b）和（2 d）表示确定性约束。在（2 c）中，表示风险水平的条，表示嵌入约束应至少具有概率。在本节中，我们最初采用通用例程来描述CC优化问题，然后使用预防控制概念进行简化，这是电力系统的常见做法。

3 算例及Matlab代码实现

3.1 算例

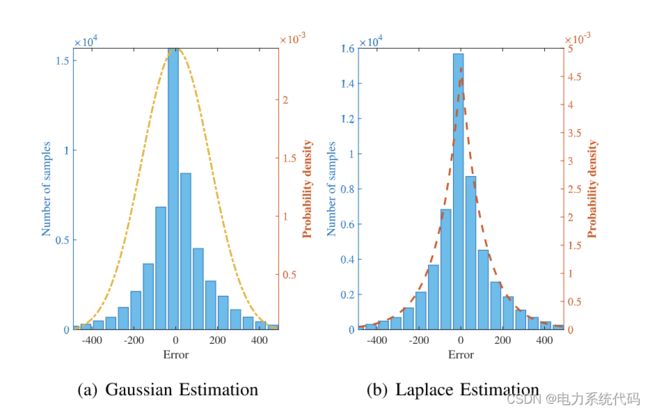
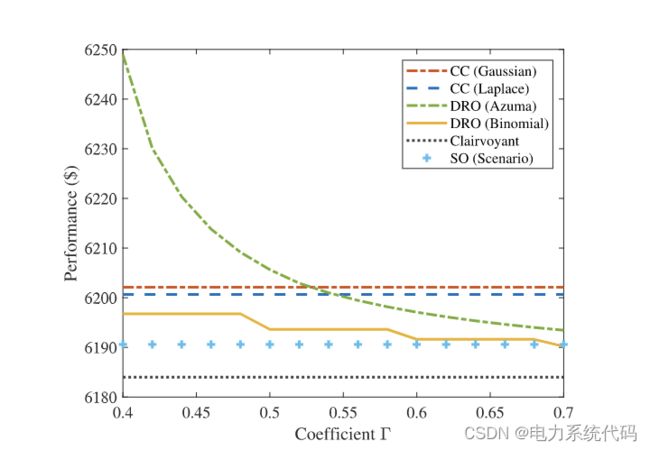
通过对改进的6节点系统和IEEE 118节点系统进行数值研究来评估所提出的方法。在第一个测试用例中，重点从数值上比较CC、DRO和透视场景，该场景认为可再生能源发电是完美的。本文数据集中提取可再生能源数据，该数据集以 5 分钟的分辨率提供有关预测和实际风能数据的信息。图 1 绘制了误差样本的直方图。对于CC问题，我们需要估计预测误差的分布模型。具体来说，采用两个单峰分布来拟合原始样本，即高斯分布和拉普拉斯分布，分别如图 1(a) 和图 1(b) 曲线所示。至于 RO，我们需要确定预期绝对预测误差的上限（即 Mn）。为了防止异常值的影响，我们只考虑 0.1-quantile 到 0.9-quantile 范围内的样本，并取所有绝对值的平均值来逼近上限。在实践中，如果允许我们在风力发电超过所选间隔时减少多余的风电或减少未履行的负荷，估计仍然有效。 

                     

                                        图1 风预报误差的高斯和拉普拉斯估计

          

                                         图3 IIIE6结构图

                                          图3 IEEE118结构图 

3.2 Matlab代码

本文仅展现部分代码，全部代码见：正在为您运送作品详情

%% 高斯分布
function [x,fval]=gen_performance_CC_Gaussian(T,N,M,bb,d_f,p,q,H,fmax,gmin,gmax,ramp_rate,epsilon,gamma,error_data,w_loc,w_num,DR,UR)
    virtual_bb=[bb bb bb];
    real_bb=zeros(N,1);
    if sum(bb)~=0
        for flag=1:1
            for k=1:w_num
                i=w_loc(k);
                virtual_bb(i,flag)= gen_virtual_storage_capacity(bb(i),epsilon,T,gamma,error_data,flag);
            end
            [standard_delta,real_bb(:,flag)]= gen_standard_delta(bb,virtual_bb(:,flag),w_loc);
        end
    end
    x=zeros(T*N*4,1);
    fval=zeros(1,1);

    for flag=1:1
        umin=-ramp_rate*real_bb(:,flag);
        umax=ramp_rate*real_bb(:,flag);
        [x(:,flag),fval(:,flag)]=MinC(T,N,M,real_bb(:,flag),d_f,p,q,H,fmax,gmin,gmax,umin,umax,DR,UR);
    end
end

3.3 结果 

 ​​​​​​​

4 写在最后 

部分理论引用网络文献，若有侵权请联系博主删除。