【数独 1】不回溯，试试候选数法1ms高效解数独谜题-C++实现

前言

不知道大家有没有玩过数独游戏，博主读高中的时候，数独曾经风靡一时，而数独作为一种数字逻辑游戏，其难度也不小，能不能用我们的计算机来解决数独问题呢？

用计算机解数独谜题最常用的方法是回溯法，如果大家想要更详细地了解回溯法，我觉得这篇文章比较思路清晰而容易理解： 链接: 回溯法解数独-知乎。接下来博主给大家介绍一种候选数法，供大家参考和交流。

一、什么是数独游戏

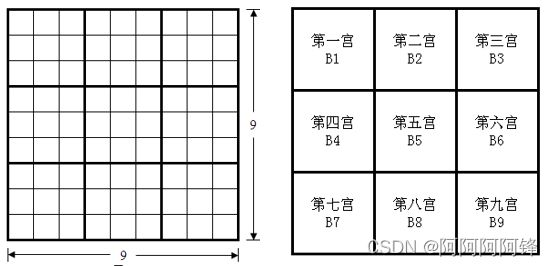
数独谜题可表示为一个9 * 9的大九宫格，它由9个小的九宫格（3 * 3格）组成。

每个谜题，81个单元格中的一部分格子会被赋予1 ~ 9中的一个数字，作为已知数字，剩余的单元格空着。数独谜题的解题就是要在空的格子中填入1 ~ 9中的数字，要求大九宫格的每一行、每一列、每一个小九宫格都包含九个不同的数字。

我们平常的数独游戏还有两个重要的特性。第一，每个数独游戏的解唯一。第二，可以通过推理来求解，即不需要列出所有可能的情况来一一行尝试。数独谜题解题的过程，就是通过已知的数字，不断推理来确定空白单元格中该填的数字的过程。

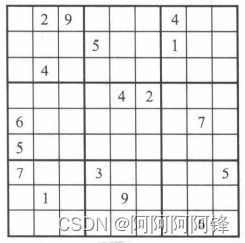
下面是一个推理过程的例子，以下图为例，数字4必须在第二行的某个单元格恰好出现一次，那么它应该在哪里呢？我们观察到，4不可能在这一行的前三个单元或后两个单元，因为4已经出现在这些单元所在小九宫格的其它单元中了；4也不能在这一行的第五个单元，因为它已经出现在这一列的其它单元中了。所以，我们可以得出结论，第二行的第6个单元中，一定是填4。

二、候选数法

每个单元格中都有1 ~ 9九个可能会填的数字，我们这些数字为该单元格的候选数。于是我们可以通过已有的数字，来删除其它单元格中的一些候选数，当某个单元格中的候选数只剩下一个时，这个单元格中的数字也就确定了。

三、设计程序

1、数独盘面和候选数在计算机中的表示

我们可以简单地用一个二维数组来表示一个数独的盘面，用一个三维数组来表示所有的候选数。

/*全局变量*/ 
//这里下标为0的位置不使用
int s[10][10]{};				//(行，列)数独的大九宫格盘面
bool p[10][10][10]{};			//(行，列，候选数字)

如： p[1][2][3] == 1 就表示第一行第二列的数字 3 候选状态，而 p[4][5][6] == 0 则表示第四行第五列填数字 6 的可能性已经被排除了。

2、算法过程

还记得数独要满足的三条规则吗？接下来就需要它们来帮助我们解数独谜题啦！
我们解一个数独谜题的过程如下：
第一步：通过给定的已知数字来删除一些候选数。对于一个已知的数字，我们删除包括处于同一行、列、小九宫的相同数字候选数，和这一单元格中的所有其它候选数。

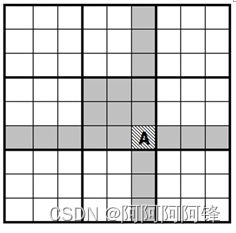
第二步：寻找只剩下一个候选数的单元格，确定该单元格中应填入的数字。
第三步：通过第二步确定的数字，继续删除候选数。
然后重复第二步和第三步，直到得到最终的答案。若在某次循环中，填入数字和候选数都不再发生变化，则停止循环，解该数独谜题就失败咯。

四、实现（C++）

了解了候选数法解数独的原理，那么接下来就和博主一起来实现它吧！

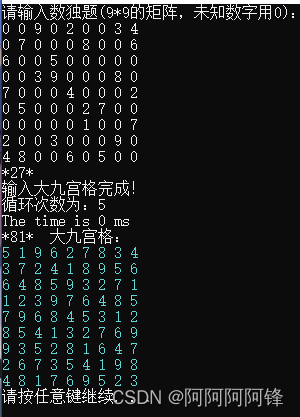
1、运行

博主将填出的数字标上了醒目的蓝色。

2、源代码

/*包含文件*/ 
#include
#include
#include
#include
#include
using namespace std;
/*全局变量*/ 
int s[10][10]{};				//(行，列)数独的大九宫格
bool p[10][10][10]{};			//(行，列，候选数字)
/*函数声明*/
void init_p();					//初始化p，置1
void init_s();   				//将s置0
void out_p();					//输出p
void in_s();					//输入数独谜题，从键盘
void out_s();					//输出s
bool exam_s(int s[][10]);		//数独有效，则返回true
void change_p();				//更新p，通过扫描s 
void change_s();				//更新s，通过扫描p
void init_a(int a[], int n);	//将一个一维数组置0
bool exam_a(int a[], int n);	//验证数组a，确定是否有数字多次出现(a记录的是数字出现的次数)
int where_small(int i);			//得到小九宫格起始坐标 
int num_have();					//统计s已经填出的数				
void color(int k);				//改变颜色输出	
bool enough_s();				//s填满则返回true
/*主函数*/
int main() {
	while(true) {		//每次循环输入一个新的谜题进行求解 
		init_s();
		init_p();
		in_s();
		clock_t start(0), finish(0);
		start = clock();
		
		int i = 0;
		for(i = 0; i < 81; ++i) {		//解数独 
			change_p();
			change_s();
			if(enough_s()) break;		//已经得到解时，停止循环
		}
		
		finish = clock();
		cout << "循环次数为：" << (i + 1) << endl;
		cout << "The time is " << (finish - start) << " ms " << endl;
		
		out_s();
		system("pause");
		system("cls");
	}
	return 0;
}
// --------------------------------------------------
/*将s矩阵重新置零*/
void init_s() {
	for(int i = 1; i <= 9; ++i) {
		for(int j = 1; j <= 9; ++j) {
			s[i][j] = 0;
		}
	}
} 
// --------------------------------------------------
/*
输出s矩阵*/
void out_s() {
	const int c(11);
	cout << "*" << num_have() << "*  ";  /*已经填好的数的数量*/ 
	cout << "大九宫格：" << endl;
	for(int i = 1; i <= 9; ++i) {
		for(int j = 1; j <= 9; ++j) {
			if(s[i][j] != 0)  color(c);
			cout << s[i][j] << " ";
			color(15);					//白色 
		}
		cout << endl;
	}
} 
// --------------------------------------------------
/*
前置：在大九宫格的行，或列i 
功能：由一个数字在大九宫格的位置，得到该数字所在的小九宫格的起始位置
后置：i不变 
返回：数字所在小九宫格的起始位置的行，或列*/
int where_small(int i) {
	if(i <= 3) return 1;
	if(i <= 6) return 4;
	if(i <= 9) return 7;
} 
// --------------------------------------------------
/*
前置：一维数组a
功能：测试数组a
后置：数组不变 
返回：a数组发现无效则返回false；否则返回true*/
bool exam_a(int a[], int n) {
	for(int i = 1; i < n; ++i) {
		if(a[i] > 1) {
			return false;
		}
	}
	return true;
} 
// --------------------------------------------------
/*
前置：一维数组
后置：一维数组所有元素值为0*/
void init_a(int a[], int n) {
	for(int i = 0; i < n; ++i) {
		a[i] = 0;
	}
} 
// --------------------------------------------------
/*
前置：p数组，s数组
功能：扫描p，在s写入已经可以确定的数字
原理：大九宫格的每一行，列，小九宫格都恰好包含1~9 
后置：p不变，s部分由0变为填入的数字*/
void change_s() {
	for(int i = 1; i <= 9; ++i) {			//i迭代p中9个数值矩阵
		for(int j = 1; j <= 9; ++j) {		//行列扫描一起 
			int count_h(0), count_l(0); 	//行，列扫描中1的个数
			int m_h(0), n_h(0);  			//(m,n)为1所在坐标
			int m_l(0), n_l(0); 
			for(int k = 1; k <= 9; ++k) {
				if(p[j][k][i] == 1) {  		//一行 
					count_h++;
					m_h = j;  n_h = k;
				}
				if(p[k][j][i] == 1) {		//一列 
					count_l++;
					m_l = k;  n_l = j;
				}
			}
			/*更新s*/ 
			if(count_h == 1)
				s[m_h][n_h] = i;
			if(count_l == 1)
				s[m_l][n_l] = i;
		}
		for(int j = 1; j <= 9; j += 3) {			//(j,k)定位9个小九宫的起始格(左上角) 
			for(int k = 1; k <= 9; k += 3) {
				int count(0);
				int m(0), n(0);
				for(int u = j; u <= j + 2; ++u) {	//(u,v)迭代扫描一个小九宫 
					for(int v = k; v <= k + 2; ++v) {
						if(p[u][v][i] == 1) {
							count++;
							m = u;  n = v;
						}
					}
				} 
				/*更新s*/
				if(count == 1) {
					s[m][n] = i;
				} 
			}
		}
	}
}
// --------------------------------------------------
/*
前置：p数组，s数组
功能：通过s数组的每个已知数字，调整p数组的值
后置：p部分由1变为0，s不变*/
void change_p() {
	/*p中代表数值s[i][j]的矩阵*/ 
	for(int i = 1; i <= 9; ++i) {
		for(int j = 1; j <= 9; ++j) {
			
			/*更新p的数值矩阵的行，列*/ 
			for(int k = 1; k <= 9; ++k) {
				if(k != j) 
					p[i][k][s[i][j]] = 0;
				if(k != i)
					p[k][j][s[i][j]] = 0;
			}
			
			/*更新p的对应数字的小九宫格*/ 
			int m = where_small(i);  /*行*/ 
			int n = where_small(j);  /*列*/ 
			
			for(int k = m; k <= m + 2; ++k) {
				for(int l = n; l <= n + 2; ++l) {
					if(k == i && l == j);
					else  p[k][l][s[i][j]] = 0;
				}
			}
			
			/*更新p的所有数字矩阵的对应位置*/
			for(int k = 1; k <= 9; ++k) {
				if(s[i][j] != 0 && s[i][j] != k)
					p[i][j][k] = 0;
			}
		}
	}
}
// --------------------------------------------------
/*
测试一个数独是否有效*/
bool exam_s(int s[][10]) {
	int a[10]{};
	/*每行没有重复数字*/
	for(int i = 1; i <= 9; ++i) {
		init_a(a, 9);
		
		for(int j = 1; j <= 9; ++j) {
			a[s[i][j]] = 1;
		}
		if(exam_a(a, 9) == false) 
			return false;
	}
	/*每列没有重复数字*/
	for(int i = 1; i <= 9; ++i) {
		init_a(a, 9);
		
		for(int j = 1; j <= 9; ++j) {
			a[s[j][i]] = 1;  /*i,j改成了j,i*/
		}
		if(exam_a(a, 9) == false) 
			return false;
	}
	/*
	每个小九宫格没有重复数字
	定位小九宫格开始的位置*/ 
	for(int i = 1; i <= 9; i += 3) {
		for(int j = 1; j <= 9; j +=3) {
			init_a(a, 9);
			/*处理一个小九宫格*/ 
			for(int k = i; k <= i + 2; ++k) {
				for(int l = j; l <= j + 2; ++l) {
					a[s[k][l]] = 1;
				}
			}
			if(exam_a(a, 9) == false) 
				return false;
		}
	}
	return true;  /*没发现问题，就说明没有问题咯*/ 
} 
// --------------------------------------------------
/*
输出九个矩阵，每个矩阵代表一个值在九行九列的可能情况*/ 
void out_p() {
	for(int i(1); i <= 9; i += 3) {
		cout << "矩阵" << i << "：";
		cout << "          " << "        ";  /*10 + 8格*/ 
		cout << "矩阵" << i + 1 << "：";
		cout << "          " << "        ";
		cout << "矩阵" << i + 2 << "：" << endl;
		
		for(int j(1); j <= 9; ++j) {
			for(int k(1); k <= 9; ++k) {
				cout << p[j][k][i] << " ";
			}
			cout << "       ";  /*7格*/ 
			for(int k(1); k <= 9; ++k) {
				cout << p[j][k][i + 1] << " ";
			}
			cout << "       ";
			for(int k(1); k <= 9; ++k) {
				cout << p[j][k][i + 2] << " ";
			}
			cout << endl;
		}
		cout << endl;
	}
}
// --------------------------------------------------
/*
从键盘输入数独已知方阵信息*/
void in_s() {
	cout << "请输入数独题(9*9的矩阵，未知数字用0)：" << endl;
	for(int i(1); i <= 9; ++i) {
		for(int j(1); j <= 9; ++j) {
			cin >> s[i][j];
		}
	} 
	cout << "*" << num_have() << "*" << endl;
	cout << "输入大九宫格完成！" << endl;
}
// --------------------------------------------------
/*
前置：p中所有单元的值为0
后置：p中行、列、数字值从1到9的共729个单元的值为1，其余单元为0*/
void init_p() {
	for(int i = 1; i <= 9; ++i) {
		for(int j = 1; j <= 9; ++j) {
			for(int k = 1; k <= 9; ++k) {
				p[i][j][k] = 1;
			}
		}
	}
}
// --------------------------------------------------
/*(done)
统计s已经填出的数*/
int num_have() {
	int count(0);
	for(int i = 1; i <= 9; ++i) {
		for(int j = 1; j <= 9; ++j) {
			if(s[i][j] > 0)
				count++;
		}
	}
	return count;
}
// --------------------------------------------------
void color(int k) {		// 改变颜色输出
	SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), k); 
}
// --------------------------------------------------
bool enough_s() {		//s填满返回true 
	if(num_have() < 81) return false;
	return true;
}

五、算法分析

候选数法解数独谜题的效率确实很高，当得起“高效”而字，基本上可以在1ms内就得到解。
但可能有的小伙伴已经发现了问题，“博主，你怎么证明你的算法一定能够得到一个数独谜题的解？”确实，在博主对程序的测试中发现，有一些数独谜题该算法是无法得到解的，这也让博主感到十分遗憾。

六、总结

虽然该算法的能力有点弱哈，但博主感觉这也是对自己生活中问题的一次有趣的尝试呀。从一开始，用候选数法得到数独谜题的解就只是一个猜想。看到它确实能够解决一部分的数独问题，博主已经挺开心啦！

数独题库：尤怪之家数独挑战馆出题菜单
里面的数独题非常丰富哦！有兴趣的小伙伴可以看一看。

附录（测试数据）

直接复制到程序运行框可能行末会缺少换行，可以先复制到记事本。
0 0 9 0 2 0 0 3 4
0 7 0 0 0 8 0 0 6
6 0 0 5 0 0 0 0 0
0 0 3 9 0 0 0 8 0
7 0 0 0 4 0 0 0 2
0 5 0 0 0 2 7 0 0
0 0 0 0 0 1 0 0 7
2 0 0 3 0 0 0 9 0
4 8 0 0 6 0 5 0 0

0 0 0 0 0 7 3 0 8
2 0 0 0 0 0 0 0 7
0 9 7 8 0 5 6 0 0
0 7 0 1 0 0 9 0 6
0 0 5 9 0 3 7 0 0
9 0 1 0 0 8 0 3 0
0 0 2 3 0 4 5 6 0
8 0 0 0 0 0 0 0 1
5 0 4 2 0 0 0 0 0

1 0 0 0 4 0 0 0 7
0 5 0 0 0 2 0 9 0
0 0 8 0 0 0 4 0 0
0 7 0 2 0 0 0 0 8
0 0 6 0 9 0 1 0 0
3 0 0 0 0 8 0 5 0
0 0 1 0 0 0 6 0 0
0 2 0 8 0 0 0 4 0
6 0 0 0 3 0 0 0 5

8 5 0 0 0 0 2 0 0
0 6 0 0 0 0 0 1 0
0 0 1 0 0 0 4 3 7
0 0 0 3 0 2 0 0 0
0 0 5 0 8 0 9 0 0
0 0 0 7 0 1 0 0 0
5 8 6 0 0 0 3 0 0
0 2 0 0 0 0 0 5 0
0 0 7 0 0 0 0 4 6

有什么问题都可以在评论区提出来和博主一起交流。
如果博主的文章对你有帮助，收藏加关注，好文不迷路哦！

下一篇中做了一些改进：【数独 2】候选数法解数独谜题-挖掘更深的信息-C++实现