【废话外传】：终于要讲神经网络了，这个让我踏进机器学习大门，让我读研，改变我人生命运的四个字！话说那么一天，我在乱点百度，看到了这样的内容：
看到这么高大上，这么牛逼的定义，怎么能不让我这个技术宅男心向往之？现在入坑之后就是下面的表情：
好了好了，玩笑就开到这里，其实我是真的很喜欢这门学科，要不喜欢，老子早考公务员，找事业单位去了，还在这里陪你们牛逼打诨？写博客，吹逼？
1神经网络历史（本章来自维基百科，看过的自行跳过）
沃伦·麦卡洛克和沃尔特·皮茨（1943）[基于数学和一种称为阈值逻辑的算法创造了一种神经网络的计算模型。这种模型使得神经网络的研究分裂为两种不同研究思路。一种主要关注大脑中的生物学过程，另一种主要关注神经网络在人工智能里的应用。
赫布型学习
二十世纪40年代后期，心理学家唐纳德·赫布根据神经可塑性的机制创造了一种对学习的假说，现在称作赫布型学习。赫布型学习被认为是一种典型的非监督式学习规则，它后来的变种是长期增强作用的早期模型。从1948年开始，研究人员将这种计算模型的思想应用到B型图灵机上。
法利和韦斯利·A·克拉克（1954）[3]首次使用计算机，当时称作计算器，在MIT模拟了一个赫布网络。
弗兰克·罗森布拉特（1956）[4]创造了感知机。这是一种模式识别算法，用简单的加减法实现了两层的计算机学习网络。罗森布拉特也用数学符号描述了基本感知机里没有的回路，例如异或回路。这种回路一直无法被神经网络处理，直到Paul Werbos(1975)创造了反向传播算法。
在马文·明斯基和西摩·帕尔特（1969）发表了一项关于机器学习的研究以后，神经网络的研究停滞不前。他们发现了神经网络的两个关键问题。第一是基本感知机无法处理异或回路。第二个重要的问题是电脑没有足够的能力来处理大型神经网络所需要的很长的计算时间。直到计算机具有更强的计算能力之前，神经网络的研究进展缓慢。
反向传播算法与复兴[编辑]
后来出现的一个关键的进展是反向传播算法（Werbos 1975）。这个算法有效地解决了异或的问题，还有更普遍的训练多层神经网络的问题。
在二十世纪80年代中期，分布式并行处理（当时称作联结主义）流行起来。David E. Rumelhart和James McClelland（1986）的教材对于联结主义在计算机模拟神经活动中的应用提供了全面的论述。
神经网络传统上被认为是大脑中的神经活动的简化模型，虽然这个模型和大脑的生理结构之间的关联存在争议。人们不清楚人工神经网络能多大程度地反映大脑的功能。
支持向量机和其他更简单的方法（例如线性分类器）在机器学习领域的流行度逐渐超过了神经网络，但是在2000年代后期出现的深度学习重新激发了人们对神经网络的兴趣。
2006年之后的进展[编辑]
人们用CMOS创造了用于生物物理模拟和神经形态计算的计算装置。最新的研究显示了用于大型主成分分析和卷积神经网络的纳米装置[5]具有良好的前景。如果成功的话，这会创造出一种新的神经计算装置[6]，因为它依赖于学习而不是编程，并且它从根本上就是模拟的而不是数字化的，虽然它的第一个实例可能是数字化的CMOS装置。
在2009到2012年之间，Jürgen Schmidhuber在Swiss AI Lab IDSIA的研究小组研发的递归神经网络和深前馈神经网络赢得了8项关于模式识别和机器学习的国际比赛。[7][8]例如，Alex Graves et al.的双向、多维的LSTM赢得了2009年ICDAR的3项关于连笔字识别的比赛，而且之前并不知道关于将要学习的3种语言的信息。[9][10][11][12]
IDSIA的Dan Ciresan和同事根据这个方法编写的基于GPU的实现赢得了多项模式识别的比赛，包括IJCNN 2011交通标志识别比赛等等。[13][14]他们的神经网络也是第一个在重要的基准测试中（例如IJCNN 2012交通标志识别和NYU的扬·勒丘恩（Yann LeCun）的MNIST手写数字问题）能达到或超过人类水平的人工模式识别器。
类似1980年Kunihiko Fukushima发明的neocognitron[15]和视觉标准结构[16]（由David H. Hubel和Torsten Wiesel在初级视皮层中发现的那些简单而又复杂的细胞启发）那样有深度的、高度非线性的神经结构可以被多伦多大学杰夫·辛顿实验室的非监督式学习方法所训练
现在的发展：
谷歌阿法狗战胜李世石，深度学习火的不要不要的。
。
二 神经网络的原理
1 人工神经元与神经元
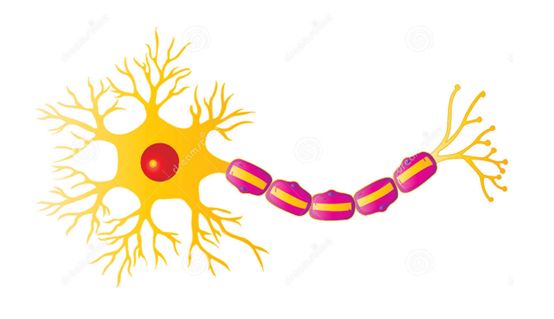
众所周知，人是靠神经元控制身体的运转的。例如下图：
你看这边大头的，就是我们的输入，经过处理，后面的就是我们的输出，这个输出有可能又接着其他的输入，最后形成这样：
然后信息就这样被传播下去了，人体是这样传播的，那我们的人造神经网络是什么样的呢，当然也和这个差不多了。
现在人们提出的神经元模型有很多，其中最早提出并且影响最多的是1943年心理学家
McCullocl和数学家W.Pitts在分析总结神经元基本特性的基础上首先提出的MP模型。该
模型经过不断改进后，形成现在广泛应用的BP神经元模型(朱人奇提出，2006)。人工神经元模型是由大量处理单元广泛互连而成的网络，是人脑的抽象、简化、模拟，反映人脑的基
本特性。一般来说，作为人工神经元模型应具各三个要素:
-
每个神经元的输入有一个权重wi用来表示第i个神经元神经元的连接权重。
-
各个信号信息乘以权重得到的信号累加器，θ表示阀值。
-
激励函数。（这个我后面讲）
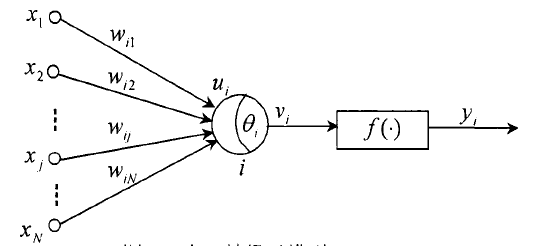
有了上述三个要素，来看看人造神经元：
其中
为神经元的初始输入，
为神经元的组合输入，即：
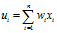，θ为阀值，vi为组合输入与阀值计算之后的输入，
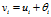。 f(x)为激励函数，激活函数，挤压函数都可以。yi是这个神经元最后的输出，
2激活函数
作用：数值上挤压，几何上变形。
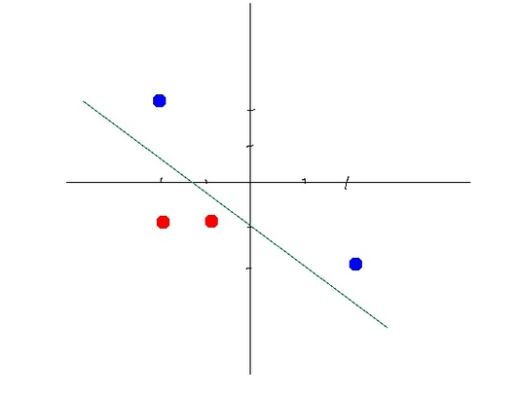
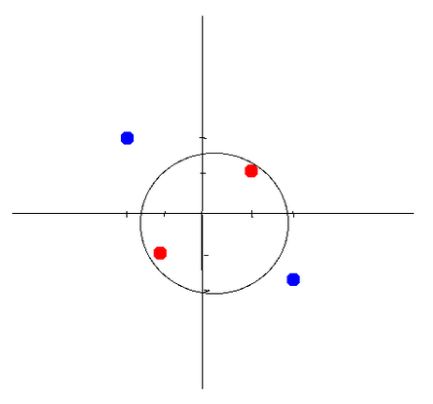
类似于这样：我们要用一条直线把下面的点区分开来：
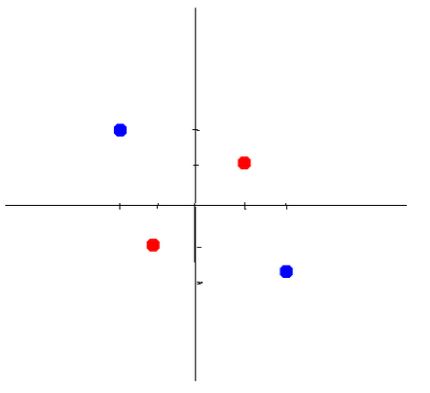
这个很容易，但是要是这样的呢？：
龟龟，这样一条直线是不是就很难分开了啊，但是要想分开，我们可以这样：把他改成非线性的不就ok了?例如先画个圆？
还有一种方法是把点投影到一个直线上，也是可以解决的。我们暂且不说。
2.1激活函数的种类
1：阀值函数
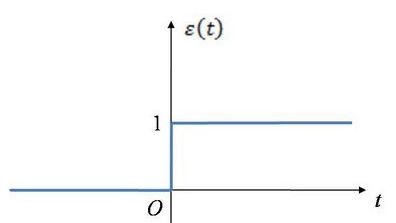
比如有时候要把很大很大的数挤压到（0,1）的范围，理想情况应该是这样：图1（本图片来自百度，反正大家都用这图）
1.
但是这个函数有个缺点只输出（0,1）是不是就降低了神经元的功效了？这就是MP模型，可以用来表示神经元的激活与非激活状态。
2 sigmoid函数
Sigmoid函数又称为s形函数，等等我好像在logistic回归中讲过这个函数，看来这个函数还是很牛逼的啊。
表达式：
图形：
我们可以通过改变a来改变函数的斜率。当斜率趋向于无穷大时候，那么这就是一个阶跃函数。Sigmoid函数可微分，但是阶跃函数却不是的。
三 BP神经网络
1 BP的基本思想
BP算法的基本思想是：学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时，输入样本从输入层传入，经各隐含层处理后，传向输出层，若输出层的实际输出与期望的输出不符合要求，则转入误差的反向传播阶段。误差反向传播是将输出误差以某种形式通过隐含层向输入层逐层反向传播，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元的依据。这种信号正向传播与误差反向传播的各层权值调整过程，是周而复始地进行的。权值不断调整的过程，也就是网络的学习训练过程。此过程一直进行到网络输出的误差减少到可接受的程度或进行到预先设定的学习次数为止。
其实就是我们小时候去给老师检查作业：老师说，不合格，拿回去修改，修改过程就是调节权重的过程，一般这个过程结束就只有，（假设老师的忍耐系数是10次）你把老师惹烦了，老师懒得理你了，就说你过了，第二种就是你达到了老师的要求了。。。你就过了，哈哈。
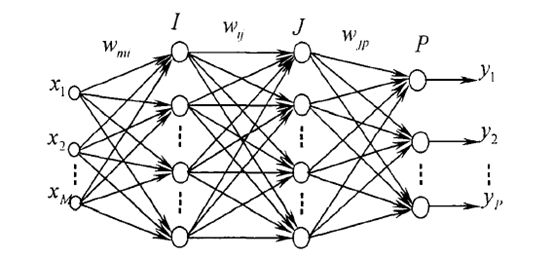
2 BP的结构
就很多神经元结合在一起，得到最后的输出，这个应该很好理解。我就不多说了。
3 BP的公式推导
以上图为例子：
训练样本集：
对任意样本集：
实际输出：
期望输出：
正向传播：
初始输入—》I层：
I层—》J层：
J层—》P层：
那么预测输出：
误差为：
定义误差能量为：
，(感觉就是方差有木有)那么神经元的误差总和：
正向过程是信号向前传播的过程，那么得到这个误差是不是就要想方设法地让误差最小，要是0才好呢。但这是不可能的，因为只要是估计预测总会有误差，就好像你去医院用B超查男女孩，也是会有误差的。所以要想更新误差就要反向传播误差信号。
反向传播过程：
-
隐层J与输出层P之间的修正量，BP算法中权重的修正量与误差的权重的偏微分成正比，即：
又因为：
又因为：
得到：
梯度为（梯度下降算法的梯度？其实本质上就是了，估计我后面写的大家也猜到了）：
根据激励函数为：
得到：
所以：
那么
修正量就可以表示为：
所以可得迭代公式为：
隐层I到J的权值修正值为（和上面照葫芦画葫芦，我就不说了）：
M层与I层：
现在BP的推导过程到这里就结束了。
4 BP的类型
BP网络的权值调整有两种模式:增量模式和批量模式。前者是指在每输入一个样本后，都回传误差一次并调整权值，后者是在所有的样本输入之后，计算网络的误差E(n),然后根据总误差计算各层信号并调整权值。由于批量模式遵循了以减小全局误差为目标的"集体主义"原则，因而可以保证总误差向减小方向变化。在样本数较多时，批量模式比增黄模式的收敛速度快。图2-7给出了批量模式的流程图。
四 BP的代码实现
1 python代码
# Back-Propagation Neural Networks
#
# Written in Python. See http://www.python.org/
# Placed in the public domain.
# Neil Schemenauer
import math
import random
import string
random.seed(0)
# calculate a random number where: a <= rand < b
def rand(a, b):
return (b-a)*random.random() + a
# Make a matrix (we could use NumPy to speed this up)
def makeMatrix(I, J, fill=0.0):
m = []
for i in range(I):
m.append([fill]*J)
return m
# our sigmoid function, tanh is a little nicer than the standard 1/(1+e^-x)
def sigmoid(x):
return math.tanh(x)
# derivative of our sigmoid function, in terms of the output (i.e. y)-derivative of tanh
def dsigmoid(y):
return 1.0 - y**2
class CBPNNClass:
def __init__(self, ni, nh, no):
# number of input, hidden, and output nodes
self.ni = ni + 1 # +1 for bias node
self.nh = nh
self.no = no
# activations for nodes
self.ai = [1.0]*self.ni
self.ah = [1.0]*self.nh
self.ao = [1.0]*self.no
# create weights
self.wi = makeMatrix(self.ni, self.nh)
self.wo = makeMatrix(self.nh, self.no)
# set them to random vaules
for i in range(self.ni):
for j in range(self.nh):
self.wi[i][j] = rand(-0.2, 0.2)
for j in range(self.nh):
for k in range(self.no):
self.wo[j][k] = rand(-2.0, 2.0)
# last change in weights for momentum
self.ci = makeMatrix(self.ni, self.nh)
self.co = makeMatrix(self.nh, self.no)
def update(self, inputs):
if len(inputs) != self.ni-1:
raise ValueError('wrong number of inputs')
# input activations
for i in range(self.ni-1):
#self.ai[i] = sigmoid(inputs[i])
self.ai[i] = inputs[i]
# hidden activations
for j in range(self.nh):
sum = 0.0
for i in range(self.ni):
sum = sum + self.ai[i] * self.wi[i][j]
self.ah[j] = sigmoid(sum)
# output activations
for k in range(self.no):
sum = 0.0
for j in range(self.nh):
sum = sum + self.ah[j] * self.wo[j][k]
self.ao[k] = sigmoid(sum)
return self.ao[:]
def backPropagate(self, targets, N, M):
if len(targets) != self.no:
raise ValueError('wrong number of target values')
# calculate error terms for output
output_deltas = [0.0] * self.no
for k in range(self.no):
error = targets[k]-self.ao[k]
output_deltas[k] = dsigmoid(self.ao[k]) * error
# calculate error terms for hidden
hidden_deltas = [0.0] * self.nh
for j in range(self.nh):
error = 0.0
for k in range(self.no):
error = error + output_deltas[k]*self.wo[j][k]
hidden_deltas[j] = dsigmoid(self.ah[j]) * error
# update output weights
for j in range(self.nh):
for k in range(self.no):
change = output_deltas[k]*self.ah[j]
self.wo[j][k] = self.wo[j][k] + N*change + M*self.co[j][k]
self.co[j][k] = change
#print N*change, M*self.co[j][k]
# update input weights
for i in range(self.ni):
for j in range(self.nh):
change = hidden_deltas[j]*self.ai[i]
self.wi[i][j] = self.wi[i][j] + N*change + M*self.ci[i][j]
self.ci[i][j] = change
# calculate error
error = 0.0
for k in range(len(targets)):
error = error + 0.5*(targets[k]-self.ao[k])**2
return error
def test(self, patterns):
for p in patterns:
print(p[0], '->', self.update(p[0]))
def weights(self):
print('Input weights:')
for i in range(self.ni):
print(self.wi[i])
print()
print('Output weights:')
for j in range(self.nh):
print(self.wo[j])
def train(self, patterns, iterations=1000, N=0.5, M=0.1):
# N: learning rate
# M: momentum factor
for i in range(iterations):
error = 0.0
for p in patterns:
inputs = p[0]
targets = p[1]
self.update(inputs)
error = error + self.backPropagate(targets, N, M)
if i % 100 == 0:
print('error %-.5f' % error)
def demo():
# Teach network XOR function
pat = [
[[0,0], [0]],
[[0,1], [1]],
[[1,0], [1]],
[[1,1], [0]]
]
# create a network with two input, two hidden, and one output nodes
n = CBPNNClass(2, 2, 1)
# train it with some patterns
n.train(pat)
# test it
n.test(pat)
if __name__ == '__main__':
demo()
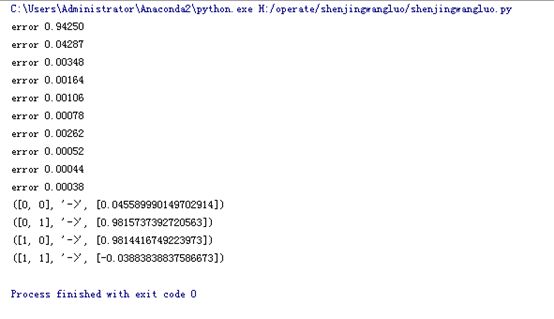
2运行结果
五 BP的缺点
(1 ) BP学习算法采用梯度下降法来收敛实际输出与期望输出之间误差。因为误差是高
维权向量的复杂非线性函数，故易陷入局部极小值;
(2)网络在学习过程收敛速度慢;
(3)在网络训练过程中容易发生振荡，导致网络无法收敛;
(4)网络的结构难以确定(包括隐层数及各隐层节点数的确定);
(5)在学习新样本时有遗忘以学过样本的趋势，因为每输入一个样本，网络的权值就
要修改一次。
(6)学习样本的数量和质量影响学习效果(主要是泛化能力)和学习速度。
正是因为BP网络白身的缺陷使得其在应用过程中存在一些棘手的问题，从而极大地影响了BP网络的进一步发展和应用。在上面的儿点中，前四点都是BP网络存在的最引人
注目的问题，第五点也是很有研究价值的一个内容。其实现在还有很多的发展，但是这个毕竟是最经典的算法，我就拿来说说。
六 后续总结
为什么我不说现在火的深度学习呢。。。。因为我感觉深度学习属于大样本事件，而且无GPU不DP。而且DP之间的参数联系我不懂，也就是说DP对于我们来说就是一个黑盒子，没人知道里面是什么。。。等我有空了，我在慢慢抽出两个月好好研究DP的paper来和大家研究。
再一次说一下，能不能点个关注？？？？