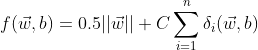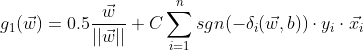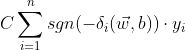Python 线性 SVM 可视化

支持向量机作为经典的二分类算法，在数学建模比赛中的优越性在于可解释性较强 —— 不像某神经网络

因为核函数的引入，会使得数据的维度增加，当维度大于 3 时无法可视化

所以在此只针对线性 SVM 进行讲解，以二维样本的二分类为例

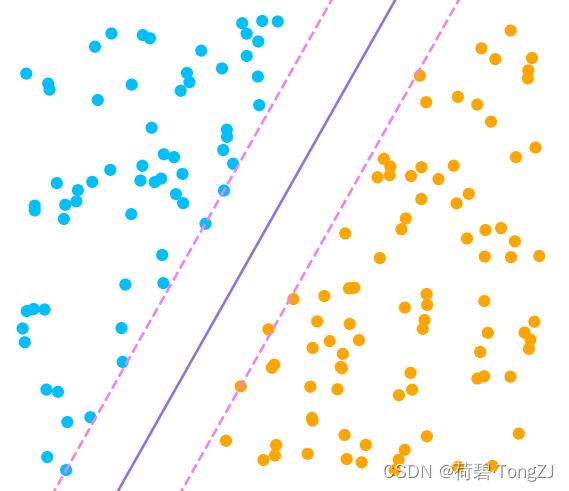
线性可分

对于该部分样本，显然有  (紫色实线) 将蓝色样本、橙色样本分离开

记每一个样本为 ，给定标签 ，该分界线 (紫色实线) 使得：

• 正样本满足 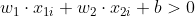，预测为 
• 负样本满足 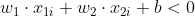，预测为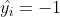 

又有两极端直线 (粉色虚线) 与分界线等距，使得：

• 正样本边界为 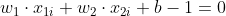，所有正样本需满足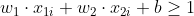 
• 负样本边界为 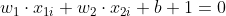，所有负样本需满足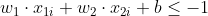 

记 ，所有样本均需满足：

当两极端直线的间隔最大时，则找到最优的分界线，根据两平行线的距离公式有：

可得 SVM 的最优化目标为：

• minimize：
• subject to：

n 维样本的二分类亦是如此，可尝试推导三维样本的分界平面

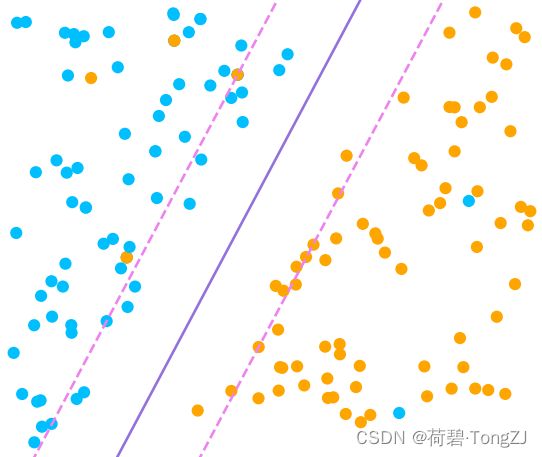
线性不可分

对该部分样本，此时已没有分界线可以完全地划分正样本、负样本

此时对约束条件做出调整，对每一个样本定义松弛变量 ，使得：

当然，松弛变量越小越好，所以此时 SVM 的最优化目标调整为：

• minimize：

其中 C 为超参数，因为  为 L2 范数正则项，所以 C 也称为正则化参数

Parameters
----------
C : float, default=1.0
    Regularization parameter. The strength of the regularization is
    inversely proportional to C. Must be strictly positive. The penalty
    is a squared l2 penalty.

C 越大，则 L2 范数正则项的系数相对越小；C 越小，则 L2 范数正则项的系数相对越大

即 C 的大小与正则化强度成反比

使用梯度下降法求解：

•  对  的偏导数为：
•  对 b 的偏导数为：
• 初始化一组  以及学习率 ，则 ，
• 当  的变化幅度较小时，即为局部最优解 

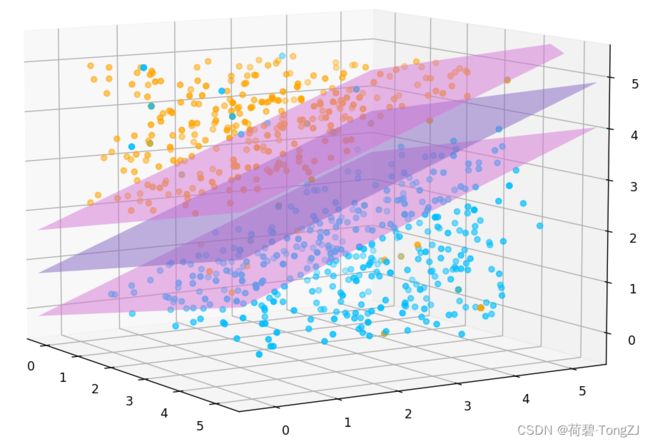
可视化

首先生成测试使用的数据集 (三维)，并给定标签，使用 sklearn 的 SVC 对象进行二分类

import random

import matplotlib.pyplot as plt
import numpy as np
from sklearn.svm import SVC


def cal_dist(x, coef=np.array([-0.5, -1, 2]), bias=-2):
    ''' 计算点到直线的距离 (保留正负号)
        Dist = (coef × x + bias) / ||coef||
            coef: [n_dim, ]
            x: [n_sample, n_dim]'''
    return (x @ coef + bias) / np.linalg.norm(coef, ord=2)


# 生成数据集
train_set = np.stack([np.random.rand(1000) * 5
                      for _ in range(3)]).T
# 保留距离预定超平面 > 0.5 的点
train_set = train_set[np.abs(cal_dist(train_set)) > 0.5]
# 根据距离的正负给定分类
train_set_label = cal_dist(train_set) > 0
random.shuffle(train_set[:100])

clf = SVC(kernel='linear')
clf.fit(train_set, train_set_label)

而分界平面的  对应 svm.coef_[0]，b 对应 svm.intercept_，由此可绘制三维分界平面 (或是二维分界线)；同理可绘制极端平面 (还有二维的极端直线)

为了把这个 3D 图画好看可费了我不少力气

def plot_hyperplane(svc, dataset, label,
                    scatter_color=['deepskyblue', 'orange'],
                    plane_color=['mediumpurple', 'violet']):
    ''' svc: 线性支持向量机实例
        dataset: 数据集, [n_sample, n_dim]
        label: 数据标签, [n_sample, ]
        scatter_color: 负样本、正样本散点颜色
        plane_color: 分界超平面、极端超平面颜色'''
    # 读取超平面参数
    coef, bias = svc.coef_[0], svc.intercept_
    # 各个维度的上下限
    n_dim = len(coef)
    limit = np.array([(dataset[:, i].min(), dataset[:, i].max())
                      for i in range(n_dim)])
    # 上下限扩充: 防止位于边界上的样本点被截掉
    extension = (limit[:, 1] - limit[:, 0]) * 0.1
    limit[:, 0] -= extension
    limit[:, 1] += extension
    # 绘制 2D 图像
    if n_dim == 2:
        fig = plt.subplot()
        coef_x, coef_y = coef
        # 找到直线的两个顶点
        x = limit[0]
        cal_y = lambda x, b: - (coef_x * x + b) / coef_y
        # 绘制分界直线
        if plane_color[0]:
            y = cal_y(x, bias)
            plt.plot(x, y, color=plane_color[0])
        # 绘制极端直线
        if plane_color[1]:
            for b_ in [-1, 1]:
                y = cal_y(x, bias + b_)
                plt.plot(x, y, color=plane_color[1], linestyle='--')
        # 裁剪画布边界
        for lim, func in zip(limit, [plt.xlim, plt.ylim]):
            func(lim)
    # 绘制 3D 图像
    elif n_dim == 3:
        fig, opacity = plt.subplot(projection='3d'), 0.5
        coef_x, coef_y, coef_z = coef
        # 定义计算 z 的函数
        cal_z = lambda x, y, b: - (coef_x * x + coef_y * y + b) / coef_z

        def get_vex(b):
            x, y = np.meshgrid(*limit[:2])
            x, y = x.reshape(-1), y.reshape(-1)
            z = cal_z(x, y, b)
            # Δz: z - Δz ∈ [z_min, z_max]
            z_min, z_max = limit[2]
            delta_z = (z > z_max) * (z - z_max) + (z < z_min) * (z - z_min)
            # subject to: coef_x·Δx + coef_y·Δy + coef_z·Δz = 0
            delta_x = - coef_z * delta_z / coef_x
            x_ = x - delta_x
            delta_y = - coef_z * delta_z / coef_y
            y_ = y - delta_y
            # 获得新的点集
            x = np.stack([x, x_], axis=-1).reshape(-1)
            y = np.stack([y_, y], axis=-1).reshape(-1)
            # 剔除相同的点
            points = np.unique(np.stack([x, y], axis=-1), axis=0)
            points = np.concatenate([points, points[-1].reshape(1, -1)]) if len(points) & 1 else points
            # 定义平面的顶点
            x, y = points.T.reshape(2, 2, -1)[..., ::-1]
            return x, y, cal_z(x, y, b)

        # 绘制分界平面
        if plane_color[0]:
            fig.plot_surface(*get_vex(bias), alpha=opacity, color=plane_color[0])
        # 绘制极端平面
        if plane_color[1]:
            for b_ in [-1, 1]:
                fig.plot_surface(*get_vex(bias + b_), alpha=opacity, color=plane_color[1])
        # 裁剪画布边界
        for lim, func in zip(limit, [fig.set_xlim3d, fig.set_ylim3d, fig.set_zlim3d]):
            func(lim)
    else:
        raise AssertionError(f'不支持{n_dim}维数据的可视化')
    # 绘制样本散点
    if scatter_color:
        scatter_color = scatter_color * 2 if len(scatter_color) == 1 else scatter_color
        fig.scatter(*[dataset[:, i] for i in range(n_dim)],
                    color=[scatter_color[l] for l in map(int, label)])


plot_hyperplane(clf, train_set, train_set_label)
plt.show()