python数据分析学习和建模的个人笔记（一）

自己用的一些常用知识点（Python数据分析+可视化）

Numpy模块————————————————————————

1.多维数组嵌套用都为()或[],主要每个（元素相同，否则索引可能出错）

arr = np.array(((64, 95, 46, 27), (88, 4, 11, 96)
                , (21, 72, 20, 10), (44, 38, 2, 7)))
arr = np.array([[64, 95, 46, 27], [88, 4, 11, 96]
                   , [21, 72, 20, 10], [44, 38, 2, 7]])
print(arr)

2.多维数组切片索引(解决弊端：arr[np.ix_(索引)] )

arr = np.array(((64, 95, 46, 27), (88, 4, 11, 96)
                , (21, 72, 20, 10), (44, 38, 2, 7)))
print(arr[3, 1])  # 根据下标
print(arr[2, :])  # 第三个数组的全部元素
print(arr[1:4, 1:4])  # 取下标1、2、3数组，取数组中下标1，2，3元素```

3.数组常用的属性

"""
fname:数据文件路径
dtype：读入数据类型，默认float
comments：指定注释符，默认#
delimiter：指定数据集的列分割符
skip_header,skip_footer：是否跳过数据集首行、脚注，默认不跳过
converters：指定列数据换成其他数据
missing_values,filling_values：指定缺失标记,如果原数据有标记则读入后为缺失值;填充缺失值
usecols:指定读入那列
names：读入数据的列设置名称
"""
np.genfromtxt(fname,dtype,comments,delimiter,skip_header,skip_footer,
              converters,missing_values,filling_values,usecols=,names)

4.1数组形状处理

arr = np.array([[64, 95, 46, 27], [88, 4, 11, 96]
                   , [21, 72, 20, 10], [44, 38, 2, 7]])

'''
reshape：未直接改变数组
resize：直接改变数组形态
'''
print(arr.shape)  # 元组形式返回数组的行列数
print(arr.reshape(2, 8))  # 变成2个数组，8个元素
print(arr.shape)
print(arr.resize(2, 8))  # 不会返回数组
print(arr.shape)```

4.2数组的降维兼并排序

'''
数组降维:ravel,flatten,reshape
'''
# 变成一维数组
print(arr.ravel())
print(arr.flatten())
print(arr.reshape(-1))
# 降维同时排序
print(arr.ravel(order='F'))
print(arr.reshape(-1, order='F'))
print(arr.flatten(order='F'))

4.3数组的改变值

arr = np.array([[64, 95, 46, 27], [88, 4, 11, 96]
                   , [21, 72, 20, 10], [44, 38, 2, 7]])

arr.flatten()[0] = 2000  # 无影响
print(arr)
arr.ravel()[1] = 1000  # 影响数组
print(arr)
arr.reshape(-1)[2] = 2000  # 影响数组
print(arr)

4.4数组的叠数组（记忆对应（vstack:hstack）==(row_stack:column_stack)）

arr = np.array([[64, 95, 46, 27], [88, 4, 11, 96]
                   , [21, 72, 20, 10], [44, 38, 2, 7]])
# 纵向堆叠数组
arr2 = np.array([1, 2, 3, 4])
print(np.vstack([arr, arr2]))
print(np.row_stack([arr, arr2]))
# 横向合并数组
arr3 = np.array([[1], [2], [3], [4]])
print(np.hstack([arr, arr3]))
print(np.column_stack([arr, arr3]))

5.数组计算
+(add), -(subtract), *(multiply), /(divide)
比较运算符一样：特殊用法是取子集

math = np.array([98, 83, 86, 92, 67, 82])
english = np.array([68, 74, 66, 82, 75, 89])
chinese = np.array([92, 83, 76, 85, 87, 77])
print(np.add(np.add(math, chinese), english))
print(np.subtract(math+10, chinese))
print(np.multiply(math+10, english))
print(np.divide(english*10, chinese))
print(math % 10)  # 求余数
print(math // 70)  # 整除
print(math ** 2)  # 指数
# ---------------------------------------比较运算符
print(math[math > english])  # 对应的下标元素比较
print(english[english < chinese])
print(english[english >= chinese])
print(math[math == chinese])
print(math[math != chinese])

6.广播运算（对于数组形状不同也能进行运算）

在这里插入代码片

7.数组的 数学函数于统计函数

数学函数	函数说明	统计函数	函数说明
np.pi	常数π	np.min(arr,axis)	按照轴的方向计算最小值
np.e	常数e	np.max(arr,axis)	按照轴的方法计算最大值
np.fabs(arr)	计算各元素的浮点型绝对值	np.mean(arr,axis)	按照轴的方法计算平均值
np.floor(arr)	对各个元素向上取整	np.median(arr,axis)	计算中位数
np.round(arr)	对各个元素向下取整	np.sum(arr,axis)	计算和
np.fmod(arr1,arr2)	对各元素四舍五入	np.std(arr,axis)	标准差
np.modf(arr)	计算arr1/arr2的余数	np.var(arr,axis)	方差
np.sqrt(arr)	返回数组元素的小数部分和整数部分	np.cumsum(arr,axis)	累计和
np.square(arr)	计算各元素的算术平方根	np.cumprod(arr,axis)	累计乘积
np.exp(arr)	计算各元素的平方根	np.argmin(arr,axis)	最小值所在位置
np.power(arr,num)	计算各元素的指数	np.argmax(arr,axis)	最大值所在位置
np.log2(arr)	计算以2为底的对数	np.corrcoef(arr)	计算皮尔逊相关系数
np.log10(arr)	计算以10为底的对数	np.cov(arr)	计算协方差矩阵
np.log(arr)	计算以e为底的各元素的对数

8.线性代数的相关计算

函数	说明	函数	说明
np.zeros	生成零矩阵	np.ones	生成所有元素为1的矩阵
np.eye	生成单位矩阵	np.transpose	矩阵转置
np.dot	计算两个数组的点积	np.inner	计算两个数组的内积
np.diag	矩阵主对角线与一维数组间的转换	np.trace	矩阵主对角线元素的和
np.linalg.det	计算矩阵行列式	np.linalg.eig	计算矩阵特征根与特征向量
np.linalg.eigvals	计算方阵特征根	np.linalg.inv	计算方阵的逆
np.linalg.pinv	计算方阵的Moore-Penrose伪逆	np.linalg.solve	计算Ax=b的线性方程组的解
np.linalg.lstsq	计算Ax=b的最小二乘解	np.linalg.qr	计算QR分解
np.linalg.svd	计算奇异值分解	np,linalg.norm	计算向量或矩阵的范数

# 1.dot函数的使用
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
print(np.dot(arr1, arr2))  # 一维数组的点积
arr3 = np.array([[1, 2, 3], [4, 5, 6]])
arr4 = np.array([[7, 8], [1, 9], [2, 8]])
# 二维数组为矩阵相乘：第一个矩阵列=第二矩阵行
print(np.dot(arr3, arr4))

# 2.diag函数的使用
arr5 = np.arange(16).reshape(4, 4)  # 4x4矩阵
print(arr5)
print(np.diag(arr5))  # 取出矩阵对角线
print('用一维数组组成的矩阵\n', np.diag(np.array([5, 15, 25])))

# 3.特征根和特征向量
arr6 = np.array([[1, 2, 5], [3, 6, 8], [4, 7, 9]])
print('3x3的矩阵的特征根：\n', np.linalg.eig(arr6)[0], '\n特征向量:\n', np.linalg.eig(arr6)[1])

# 4.多元线性回归模型的解（预测连续的因变量）天气、游客、城市收入等
x = np.array([[1, 1, 4, 3], [1, 2, 7, 6], [1, 2, 6, 6], [1, 3, 8, 7],
              [1, 2, 5, 8], [1, 3, 7, 5], [1, 6, 10, 12],
              [1, 5, 7, 7], [1, 6, 3, 4], [1, 5, 7, 8]])
y = np.array([3.2, 3.8, 3.7, 4.3, 4.4, 5.2, 6.7, 4.8, 4.2, 5.1])
x_trans_X_inverse = np.linalg.inv(np.dot(np.transpose(x), x))  # 计算矩阵的逆(计算矩阵的相乘(矩阵转置[行列调换]))
print(np.dot(np.dot(x_trans_X_inverse, np.transpose(x)), y))  # 计算偏回归系数

# 5.多元一次方程组的求解
# 2x+3y+z=34
# 3x+2y+z=39
# x+2y+3z=26
A = np.array([[3, 2, 1], [2, 3, 1], [1, 2, 3]])
B = np.array([39, 34, 26])
print(np.linalg.solve(A, B))

# 6.范数的计算
arr7 = np.array([1, 3, 5, 7, 9, 10, -12])
print(np.linalg.norm(arr7, ord=1))  # 向量的第一范式
print(np.linalg.norm(arr7, ord=2))  # 向量的第二范式
print(np.linalg.norm(arr7, ord=np.inf))  # 向量的第n范式

8.伪随机数的生成

函数	说明	函数	说明
seed(n)	设置随机种子	multinomial(n,pvals,size=None)	生成多项分布随机数
beta(a,b,size=None)	生成贝塔分布随机数	multivariate_normal(mean,cov[,size)	生成多元正态分布随机数
chisquare(df,size=None)	生成卡方分布随机数	normal(loc=0.0,scal=1.0,size=None)	生成正态分布随机数
choice(a,size=None,replace=True,p=None)	从a中有放回地随机挑选指定数量的样本	pareto(a,size=None)	生成帕累托分布随机数
exponential(scale=1.0,size=None)	生成指数分布随机数	poisson(lam=1.0,size=None)	生成泊松分布随机数
f(dfnum,dfden,size=None)	生成F分别随机数	rand(d0,d1,…,dn)	生成n维的均匀分布随机数
gamma(shap,scale=1.0,size=None)	生成伽马分布随机数	randn(d0,d1…,dn)	生成n维的标准正态分布随机数
geometric(p,size=None)	生成几何分布随机数	randint(low,high=None,size=None,dtype='l)	生成指定范围的随机整数
hypergeometric(ngood,nbad,nsample,size=None)	生成超几何分布随机数	random_sample(size=None)	生成[0,1)的随机数
laplace(loc=0.0,scale=1.0,size=None)	生成拉普拉斯分布随机数	standard_t(df,size=None)	生成标准的t分布随机数
logistic(loc=0.0,scale=1.0,size=None)	生成Logistic分布随机数	uniform(low=0.0,high=1.0,size=None)	生成指定范围的均匀分布随机数
lognormal(mean=0.0,sigma=1.0,size=None)	生成对数正态分布随机数	wald(mean,scale,sezi=None)	生成Wald分布随机数
negative_binomial	生成负二项分布随机数	weibull(a,size=None)	生成Weibull分布随机数

# 生成各种正态分布随机数
np.random.seed(1234)
rn1 = np.random.normal(loc=0, scale=1, size=1000)  # 正态分布随机数
rn2 = np.random.normal(loc=0, scale=2, size=1000)
rn3 = np.random.normal(loc=2, scale=3, size=1000)
rn4 = np.random.normal(loc=5, scale=3, size=1000)
plt.style.use('ggplot')  # 设置风格
'''
使用Seaborn
scipy的stats包含一些比较基本的工具，比如：t检验，正态性检验，卡方检验之类，
statsmodels提供了更为系统的统计模型，包括线性模型，时序分析，还包含数据集，做图工具等等
hist:区域填充颜色   kde:线条附加颜色
'''
sns.distplot(rn1, hist=False, kde=False, fit=stats.norm,
             fit_kws={'color': 'black', 'label': 'u=0,s=1', 'linestyle': '--'})
sns.distplot(rn2, hist=False, kde=False, fit=stats.norm,
             fit_kws={'color': 'b', 'label': 'u=0,s=2', 'linestyle': ':'})
sns.distplot(rn3, hist=False, kde=False, fit=stats.norm,
             fit_kws={'color': 'r', 'label': 'u=2,s=3', 'linestyle': '--'})
sns.distplot(rn4, hist=False, kde=False, fit=stats.norm,
             fit_kws={'color': 'pink', 'label': 'u=5,s=3', 'linestyle': '-.'})
plt.legend()
plt.show()

Pandas模块————————————————————————

一、序列与数据框的构造

1.构造序列

'''
1.构造序列:
   四种：1.通过同质的列表或元组构建
        2.通过字典构建
        3.通过numpy中的一维数组构建
        4.通过数据框DataFrame中的某一列构建
'''

gdp1 = pd.Series([2.8, 3.01, 8.99, 8.59, 5.18])
gdp2 = pd.Series({'北京': 2.8, '上海': 3.01, '广东': 8.99, '江苏': 8.59, '浙江': 5.18})
gdp3 = pd.Series(np.array([2.8, 3.01, 8.99, 8.59, 5.18]), index=['A', 'B', 'C', 'D', 'E'])
print(gdp1[[0, 3, 4]])
print(gdp2[[0, 3, 4]])
print(gdp3[3])

print(np.log(gdp1))  # 去e为底的对数
print(np.mean(gdp1))  # 平均数
print(gdp1.mean())  # 平均数

2.构造数据框

'''
2.构造数据框
    1.通过嵌套的列表或元组构造
    2.通过字典构造
    3.通过二维数组构造
    4.通过外部数据的读取构造
'''
df1 = pd.DataFrame([['张三', 23, '男'], ['李四', 27, '女'], ['王二', 26, '女']])
df2 = pd.DataFrame({'姓名': ['张三', '李四', '王二'], '年龄': [23, 27, 26], '性别': ['男', '女', '女']})
df3 = pd.DataFrame(np.array([['张三', 23, '男'], ['李四', 27, '女'], ['王二', 26, '女']]))

print('通过列表或元组构造:\n', df1)
print('通过字典构造：\n', df2)
print('通过二维数组构造：\n', df3)

3.DadaDrame的参数：data[数据],index[行标签],colums[列标签]

np = [[0.987849, 5.767258, 'Uncertain', 5.342334, 1]
    , [0.986684, 6.145622, 'Uncertain', 5.347108, 0], [0.988263, 5.897676, 'Uncertain', 5.676754, 1]
    , [0.984351, 4.805741, 'Uncertain', 4.875197, 0], [0.986877, 5.551835, 'Uncertain', 4.948760, 0]]
df = pd.DataFrame(data=np, index=[328, 329, 330, 331, 332], columns=['age', 'tau', 'Class', 'SOD', 'male'])
print(df)

二、外部数据的读取

1.文本文件的读取

参数	说明	参数	说明
filepath_or_buffer	文件的具体路径	skiprows	跳过原数据集的开头的行数
sep	指定原始数据中各个字段的分隔符，默认为tab制表符	skipfoorer	跳过原始数据集的末尾的行数
header	是否需要将原数据集的第一行作为表头，默认将第一行用作字段名称	nrows	读取取数据的行数
names	给数据框添加具体的表头	na_values	指定原始数据集中那些特征的值作为缺失值
index_col	指定原始数据集的某列作为数据框的行索引（标签）	skip_blank_lines	读取数据时是否需要跳过原数据集中的空白行，默认为True
usecols	指定读取原始数据集的那些变量名	parse_daes	参数为True时，则尝试解析数据框的行索引，如果参数为列表，则尝试解析对应的日期列，如果参数为嵌套列表，则将某些列合并为日期列，若为字典则解析对应的列（字典中的值），并生成新的字段名（字典中键）
dtype	给每个字段设置不同的数据类型	thousands	指定原始数据集中的千分位符
converters	通过字典格式，为数据集中的某些字段设置转换函数	comment	指定注释符，如遇到行首指定的注释符则跳过改行
encoding	有中文则需指定中文编码	engine=‘python’	因为’c‘引擎不支持skipfoorer，使用参数来避免警告

'''
1.文本文件的读取csv、table....
-------------------------------以下为原数据集合
数据来源：某公司人事记录表
时间范围：2017.1.1~2017.6.30

year,month,day,gender,occupation,income
1990,3,7,男,销售经理,6&000
1989,8,10,女,化妆师,8&500
#  1991,10,10,男,后端开发,13&500
1992,10,7,女,前端设计,6&500
1985,6,15,男,数据分析师,18&000

该数据集仅用作参考！
不可以用于他用！
备注于2018年2月。
--------------------------------
对以上的原数据集进行分析：
   1.去掉开头和末尾的行数，skiprows\skipfooter\engine避免警告
   2.#号一行跳过,comment
   3.千位符&转换为正常的数值类型数据,thousands
   4.中文encoding
   5.日期year,month,day转换为birthday,parse_dates={'标记':[列索引]}
'''
text = pd.read_table(r'D:\桌面\存放tup\待读取的txt数据.txt', sep=',',
                     parse_dates={
                         'birthday': [0, 1, 2]
                     },
                     skiprows=2, skipfooter=3, comment='#', encoding='utf-8'
                     , thousands='&', engine='python')
print(text)```

Matplotlib模块———————————————————————

点的类型

参数	说明	参数	说明
-	实心线	- -	虚线
-.	虚线和点构成的线	：	点构成的线

线的类型

参数（都为小写字母）	说明	参数	说明
.	实心点	o	空心点
^	朝上的空心三角形	v	朝下的空心三角形
>	朝右的空心三角形	<	朝左的空心三角形
s	空心正方形	p	空心五边形
*	空心五角星	h	空心六边形
x	叉号	d	空心菱形

修改时间刻度和时间戳

参数	说明	使用
import matplotlib as mpl	用于修改时间刻度的模块	mpl.dates.DateFormatter("%m-%d")可以自定义设置格式化日期
ax = plt.gca()	获取图的坐标信息	ax.xaxis.set_major_formatter(date_format)获取自定义日期格式格式，对坐标轴标签进行修改
locator = mpl.ticker.LinearLocator(10)	设置x刻度标签出现多少次，比如这个10次（和下面的不能同时生效）	ax.xaxis.set_major_locator(locator)，也是传给坐标信息
locator = mpl.ticker.MultipleLocator(7)	设置x刻度标签出现频率，比如这以7天为一个间隔	与上面相同

plt.style.use(参数)背景样式

bmh
classic
dark_background
fast
fivethirtyeight
ggplot
grayscale
seaborn-bright
seaborn-colorblind
seaborn-dark-palette
seaborn-dark
seaborn-darkgrid
seaborn-deep
seaborn-muted
seaborn-notebook
seaborn-paper
seaborn-pastel
seaborn-poster
seaborn-talk
seaborn-ticks
seaborn-white
seaborn-whitegrid
seaborn
Solarize_Light2
tableau-colorblind10
_classic_test

一、离散型变量的可视化

用于（App用户性别比例、某产品在各区域的销售量分布、各年龄阶段男女消费者的消费能力差异等）1.饼图、2.条形图（垂直或水平条形图、堆叠条形图、水平交错条形图）

1.饼图（pd.Series也可以画，跟matplotlib是相通的）

参数	说明	参数	说明
x	绘图的数据	radius	半径大小
explode	显示某部分突出	counterclock	是否让饼图逆时针呈现
labels	标签	wedgeprops	设置饼图内外边界属性，如边界线的粗细、颜色（键值对：linewidth,width,edgecolor…）
autopct	添加百分比显示（%.2f%%）	textprops	设置饼图的中文属性（键值对：fontsize,color…）
pctdistance	标签与圆心的百分比距离	center	指定饼图的中心位置，默认原点
shadow	是否显示影子	frame	是否显示饼图背后的图框，True则同时需要设置x、y轴的范围和饼图中心位置
labeldistance	标签与圆心的距离	startangle	饼图的初始摆放位置

# ② 绘制环形图：以绘制三环形为例
plt.figure(figsize=(8, 5), dpi=100)
x1 = [3496.57, 1161.55, 1251.09, 1961.07]
x2 = [1383.36, 775.09, 595.09, 1605.61]
x3 = [3756.56, 1623.36, 1730.51, 3255.94]

labels = ["劳动者报酬", "生产税金额", "固定资产折旧", "营业盈余"]
colors = ['pink', 'greenyellow', 'lightcoral', 'cyan']
# radius扩大圆圈（越大缩小内圈范围越大，圆圈的周长会大）
# wedgeprops=dict(edgecolor="w") 使饼状图之间产生颜色
# wedgeprops=dict(width=0.3) 使饼状图每个数据部分宽度缩小
plt.pie(x1, colors=colors, autopct="%.0f%%", radius=1.3,
        wedgeprops=dict(width=0.3, edgecolor='w'),
        startangle=90, counterclock=False, pctdistance=0.9)

plt.pie(x2, colors=colors, autopct="%.0f%%", radius=1,
        wedgeprops=dict(width=0.3, edgecolor="w"),
        startangle=90, counterclock=False, pctdistance=0.85)

plt.pie(x3, colors=colors, autopct="%.0f%%", radius=0.7,
        wedgeprops=dict(width=0.3, edgecolor="w"),
        startangle=90, counterclock=False, pctdistance=0.75)
plt.legend(labels=labels, loc="best", title="生产总值构成")

plt.title("生产总值构成的环形图")

plt.axis("equal")
plt.savefig('生产总值构成的环形图')
plt.show()

x1 = [1, 1, 1, 1, 1, 1, 1, 1]
labels = ["1号", "2号", "3号", "4号", "5号", "6号", "7号", "8号"]
colors = ['pink', 'greenyellow', 'lightcoral', 'cyan', 'red', 'blue', 'yellow', 'green']
plt.pie(x1, colors=colors, labels=labels, counterclock=False,
        startangle=90, wedgeprops=dict(width=0.3))
plt.show()
#————————————————————————————————————————————————————————————————————————
plt.figure(figsize=[12, 10], dpi=300)
explode = [0, 0, 0, 0, 0]  # 生成数据
colors = ['r', 'b', '#FF22DC', 'pink', 'yellow']  # 各个部分的颜色

plt.rcParams['font.family'] = 'SimHei'  # 中文字体
plt.rcParams['axes.unicode_minus'] = False  # 坐标轴负号乱码
plt.rcParams['font.size'] = 20  # 设置字体大小

# 构造数据
edu = [0.2515, 0.3724, 0.3336, 0.0368, 0.0057]
label = ['中专', '大专', '本科', '硕士', '其他']
# plt.style.use('ggplot')
# 画饼图
plt.pie(x=edu,  # 绘图数据（注意不是data）
        explode=explode,  # 指定部分突出
        colors=colors,  # 颜色
        labels=label,  # 标签
        labeldistance=1.1,  # 标签与圆图距离
        autopct='%.2f%%',
        counterclock=False,  # 是否为逆时针
        radius=0.9,  # 设置半径
        startangle=180,  # 设置饼图的初始角度
        wedgeprops={
            # 'width':0.3,
            'linewidth': 0.8,
            'edgecolor': 'w'
        },
        textprops={  # 设置字体文本
            'fontsize': 20,
            'color': 'black'
        }
        )
plt.legend()  # 设置图例
plt.title('各个学历：饼图')
plt.show()

2垂直或水平条件图形

参数	说明	参数	说明
x	传递数值序列，指定条形图x轴上的刻度值	yerr	参数含义如同xerr
height	传递数值序列，指定条形图y轴的高	label	指定条形图的标签，一般用以添加图例
width	指定条形图的刻度，默认为0.8	ecolor	指定条形图误差棒的颜色
bottom	用于绘制堆叠条形图	align	指定x轴标签的对齐方式，默认center，表示刻度标签居中对齐，如果设置为edge，则表示每个条形的左下角呈现刻度标签
color	指定条形图的填充色	log	bool类型参数,是否对坐标轴进行log变换，默认False
edgecolor	条形图边框的颜色	**kwargs	关键字参数，对条形图其它设置，如透明度…
linewidth	条形图边框的宽度，为0则不绘制边框	xerr	如果参数不为None，在条形图上的基础上添加误差棒
tick_label	指定条形图的刻度标签

1.垂直与水平条形图
垂直：plt.bar(x：为条形图的x轴对应设置，height：条形图的高度) 水平:plt.barh(y:为条形图在y轴的对应位置，width：条形图的长度)

# 条形图-------------------
height = [21, 6, 17, 35, 80, 15]
x = ['广西', '甘肃', '西藏', '上海', '广东', '新疆']
colors = ['pink', 'greenyellow', 'lightcoral', 'cyan', 'yellow', 'red']
plt.style.use('ggplot')
plt.bar(x=range(0, len(height)),  # x轴的值
        color=colors,  # 填充条形的颜色
        height=height,  # y轴的高度
        tick_label=x  # x轴的刻度标签名
        ,
        )
plt.ylabel('GDP总值')
for x, y in zip(range(0, len(height)), height):
    plt.text(x, y, '%.1f' % (round(y, 10)), ha='center', va='bottom')
plt.title('6个省份的GDP')
plt.show()

# 将上面的图形变成水平且降序bar -> barh height与x轴的值要转换y和width

height = [21, 6, 17, 35, 80, 15]
height = sorted(height, reverse=True)
x = ['广西', '甘肃', '西藏', '上海', '广东', '新疆']
colors = ['pink', 'greenyellow', 'lightcoral', 'cyan', 'yellow', 'red']
plt.style.use('ggplot')
plt.barh(width=height,  # x轴长度
         color=colors,  # 填充条形的颜色
         y=range(0, len(height)),  # y轴的值
         tick_label=x  # x轴的刻度标签名
         ,
         )
plt.ylabel('GDP总值')
for x, y in zip(height, range(0, len(height))):
    plt.text(x+3, y, '%.1f' % (round(x, 10)), ha='center')
plt.title('6个省份的GDP')
plt.show()

2.堆叠条形图（将几个离散型变量堆积在同一个垂直x轴上）：关键bottom :用于绘制堆叠条形图

#  堆叠条形图------------------------------------------
# 读入数据
Industry_GDP = pd.read_excel(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第6章 Python数据可视化\industry_GDP.xlsx')
# 取出四个不同的季度标签，用作堆叠条形图x轴的刻度标签
Quarters = Industry_GDP.Quarter.unique()
print('Quarters', Quarters)
# 取出第一产业的四季度值
Industry1 = Industry_GDP.GPD[Industry_GDP.Industry_Type == '第一产业']
# 重新设置行索引
print('\nIndustry1:', Industry1)
Industry1.index = range(len(Quarters))
# 取出第二产业的四季度值
Industry2 = Industry_GDP.GPD[Industry_GDP.Industry_Type == '第二产业']
# 重新设置行索引
Industry2.index = range(len(Quarters))
# 取出第三产业的四季度值
Industry3 = Industry_GDP.GPD[Industry_GDP.Industry_Type == '第三产业']
# 各季度下第一产业的条形图
plt.bar(x=range(len(Quarters)),
        height=Industry1, color='steelblue',
        label='第一产业', tick_label=Quarters)
# 各季度下第二产业的条形图
plt.bar(x=range(len(Quarters)), height=Industry2,
        bottom=Industry1, color='green', label='第二产业')
# 各季度下第三产业的条形图
plt.bar(x=range(len(Quarters)), height=Industry3,
        bottom=Industry1 + Industry2, color='pink',
        label='第三产业')
plt.legend()
plt.show()

3.水平交错条形图（与堆叠条形图相反，将几个离散型变量堆积在同个水平x轴）关键：每次的bar函数要使得向右偏移0.4个单位——（x=np.arange(len(Cities)) + bar_width）

HuRun = pd.read_excel(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第5章 Python数据处理工具--Pandas\HuRun.xlsx')
Cities = HuRun.City.unique()
Count2016 = HuRun.Counts[HuRun.Year == 2016]
Count2017 = HuRun.Counts[HuRun.Year == 2017]
bar_width = 0.4
plt.bar(x=np.arange(len(Cities)), height=Count2016,
        color='steelblue', width=bar_width)
plt.bar(x=np.arange(len(Cities)) + bar_width, height=Count2017,
        color='indianred', width=bar_width)
plt.xticks(np.arange(5) + 0.2, Cities)
plt.legend(['2016的各个城市GDP', '2017的各个城市GDP'], fontsize=12)
plt.show()

二、数值变量的可视化

用于（数据包含大量的数值型变量，在对数值变量进行探讨进行探索和分析时）1.直方图、2.核密度图、3.箱线图、4.小提琴图，5.折线图、6.面积图

1.直方图

参数	说明	参数	说明
x	指定要绘制直方图的数据	align	设置条形图边界值的对齐方式，默认为mid，还有left，right
bins	指定直方图条形的个数	orientation	设置直方图的摆放位置，默认为垂直方向
range	指定直方图数据的上下界，默认包含绘制图的最大值和和最小值	rwidth	设置直方图的宽度
normed(或density)	是否将直方图的频数（数量）转换成频率（占百分之几）	log	是否需要对绘图数据进行log变换
weights	可以为每一个数据点设置权重	color	设置直方图的填充色
cumulative	是否需要计算累计频数或频率	edgecolor	设置直方图的边框色
bottom	可以为直方图的每个条形添加准基线	label	直方图的标签
histtype	指定直方图的类型，默认为bar，还有barstacked、step、stepfilled	stacked	当有多个数据时，是否需要直方图呈堆叠摆放，默认水平摆放

Titanic = pd.read_csv(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第6章 Python数据可视化\titanic_train.csv')
# 检查年龄是否有缺失
any(Titanic.Age.isnull())
# 删除缺失值
Titanic.dropna(subset=['Age'],inplace=True)
plt.hist(x=Titanic.Age,
         bins=20,
         color='indianred',
         edgecolor='black',
         )
plt.xlabel('年龄')
plt.ylabel('频数')
plt.title('乘客年龄分布')
plt.show()

2.核密度图（展示年龄分布特征）

参数	说明	参数	说明
a	指定绘图数据，可以序列，一维数，列表	rug_kws	同理
bins	指定直方图条形的个数	fit_kws	同理
hist	bool参数，是否绘制直方图，默认True	color	指定图形颜色，除了随机分布曲线的颜色
kde	bool参数，是否绘制核密度图，默认True	vertical	bool参数，是否图形垂直显示，默认为True
rug	bool参数，是否绘制须图（如果参数密集，比较有用），默认false	norm_hist	bool类型参数，是否将频数改为频率，默认为false
fit	指定一个随机分布对象（需要scipy模块中的随机分布函数），用于绘制随机分布函数的概率密度曲线	axlabel	用于显示轴标签
hist_kws	以字典的形式传递直方图的修饰属性	label	指定图形的标签
kde_kws	以字典的形式传递核密度图的修饰属性	ax	指定子图的位置

# 直方图和核密度图，注意density将直方图设置为频率
Titanic.Age.plot(kind='hist', bins=20,
                 color='steelblue',
                 edgecolor='black',
                 density=True,
                 label='直方图')
Titanic.Age.plot(kind='kde', color='indianred',
                 label='核密度图')
plt.xlabel('年龄')
plt.ylabel('核密度值')
plt.title('乘客年龄分布')
plt.legend()
plt.show()

3.箱线图形（代码第二个：不同行政区的二手房单价对比）

plt.xticks(rotation=70) x标签左旋转70度；patch_artist=True箱子填满颜色；boxprops={‘color’:‘red’,‘facecolor’:‘blue’} 《color是箱子的线条颜色，facecolor是填充箱子的颜色》

参数	说明	参数	说明
x	指定绘制图片数据	showcaps	bool，是否显示上下须（箱线图的顶端和末端），true
notch	是否以凹口显示展示，默认False	showbox	是否显示箱体
sym	指定异常点的形状，默认+号	shhowfliers	是否显示异常值
vert	是否将箱线图垂直摆放，默认垂直摆放	boxprops	设置箱体属性
whis	指定上下须与上下四分位的距离，默认1.5倍的四分位差	labels	添加标签
positions	指定箱线图得位置，默认[0,1,2…]	filerprops	设置异常值属性
widths	指定箱形图得宽度，默认0.5	medianprops	设置中位数的属性，如线的类型、粗细等
patch_artist	bool，是否填充箱体颜色，false	meanprops	设置均值的属性（如点的大小、颜色等）
meanline	bool，是否用线的形式表示均值，false	capprops	设置箱形图得顶端和末端线条得属性的属性
showmeans	bool，是否显示均值，false	whiskerprops	设置须得属性

df = pd.DataFrame(data=[[96, 35, 46], [57, 20, 100], [64, 37, 76]]
                  , index=[1, 2, 3], columns=['语文', '数学', '英语'])
x = [df['语文'], df['数学'], df['英语']]
plt.ylim(0, 102)
plt.xticks(rotation=70)  # x标签左旋转70度
labels = ['语文', '数学', '英文']
# patch_artist=True箱子填满颜色
plt.boxplot(x, labels=labels, widths=[0.5, 0.5, 0.5], patch_artist=True
            ,boxprops={'color':'red','facecolor':'blue'})
plt.show()
# ————————————————————_——————_——_——————————————————_————_——_——_——————_——_——_——_
buildings = pd.read_excel(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第6章 Python数据可视化\sec_buildings.xlsx')
# 以行政区域进行分组
group_region = buildings.groupby('region')
# 各个行政区的房价平均价格：aggregate聚合计算，sort_values根据值排序，sort_index根据索引排序,ascending排序方式默认升序
avg_price = group_region.aggregate({
    'price_unit': np.mean  # 计算平均价格
}).sort_values('price_unit', ascending=False)  # 进行平均价格的排序
region_price = []
for region in avg_price.index:
    #  按照上面平均价格的行政区进行存储在不同的索引位置
    region_price.append(buildings.price_unit[buildings.region == region])

font = {'fontsize': 20}
plt.boxplot(
    x=region_price,
    patch_artist=True,
    showmeans=True,
    labels=avg_price.index,  # x轴的标签
    # 设置箱体属性
    boxprops={
        'color': 'steelblue',
        'facecolor': 'red'
    },
    # 设置异常点属性
    flierprops={
        'marker': 'o',
        'markerfacecolor': 'green',
        'markersize': 3
    },
    # 设置平均属性
    meanprops={
        'marker': 'D',
        'markerfacecolor': 'pink',
        'markersize': 4
    },
    # 设置中位数
    medianprops={
        'linestyle': ':',
        'color': 'orange'
    }
)
plt.ylabel('单价（元）', fontdict=font)
plt.title('不同行政区的二手房价对比', fontdict=font)
plt.show()

4.小提琴图（客户消费数据）
下面表格是以seaborn模块的参数，使用比matplotlib方便

参数	说明	参数	说明
x	指定小提琴的x轴数据	inner	指定小提琴内部数据点得形态，nox：绘制微型箱线图，quartiles：绘制四分位得分布图，point、stick：表示点或小竖条
y	指定小提琴的y轴数据	split	bool，使用hue，是否将小提琴从中间分为两个不同的部分，false
hue	指定一个分组变量	dodge	bool，使用hue，是否绘制水平交错的小提琴图，true
data	指定绘制小提琴的数据集	orient	指定小提琴图的呈现方向。默认垂直
order	传递一个字符串列表，用于分类变量的排序	linewidth	设置小提琴图的所有线的宽度
hue_order	传递一个字符串列表，用于分类变量hue值得排序	color	指定小提琴的颜色，与palette参数一起使用时无效
bw	指定核密度估计得带宽，带宽越大，密度曲线越光滑	palette	指定hue变量的区分色
scale	用于调整小提琴得左右宽度，如果为area，表示左右部分拥有相同得面积；count表示根据样本数量来调节宽度；width表示每个小提琴左右两部分拥有相同宽度	saturation	指定颜色的透明度
scale_hue	bool，是否对hue变量得每个水平做标准化处理	ax	指定子图的位置
width	使用hue时，控制宽度

# 小提琴图(使用seaborn模块方便)
plt.rcParams['font.family'] = 'SimHei'
tips = pd.read_csv(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第6章 Python数据可视化\tips.csv')
day = tips.day.unique()
print(day)
sns.violinplot(
    data=tips,  # 数据集
    x='day',
    y='total_bill',
    hue='sex',  # 指定分组变量
    hue_order=['Male', 'Female'],  # 指定hue值排序
    order=day,  # 指定x轴刻度标签得顺序
    scale='count',  # 以男女客户的样本数值调节小提琴图左右得宽度
    split=True,  # 小提琴图中间割开，形成不同的密度曲线(合成两个木耳，从中间分开)
    palette='RdBu',  # 指定不同性别对应的颜色（因为hue参数是以性别位变量）
    inner='box',  # 指定小提琴图内部数据点
    dodge=False,  # 有hue参数，是否绘制水平交错的小提琴图
)
plt.ylabel('消费数额（元）')
plt.xlabel('星期')
plt.legend(['女', '男'], loc='best')
plt.show()

5.折线图（公众号每天阅读趋势）

参数	说明	参数	说明
x	指定折线图的x轴数据	markersize
y	指定折线图的y轴数据	markeredgecolor	设置点的边框色
linestyle		markerfacecolor	点的填充色
linewidth		markeredgewidth	点的边框宽度
color		label	标签
marker	为折线图添加点的形状	alpha	透明度

# 折线图
import matplotlib as mpl  # 用于修改日期刻度
from pandas.plotting import register_matplotlib_converters  # 自定义时间戳
plt.style.use('ggplot')
plt.rcParams['font.family'] = 'SimHei'
pd.plotting.register_matplotlib_converters()  # 自定义转换时间戳不报错
wechat = pd.read_excel(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第6章 Python数据可视化\wechat.xlsx')
#  绘制人数折线图
plt.plot(
    wechat.Date,
    wechat.Counts,
    color='indianred',
    linestyle='-',
    linewidth=2,
    marker='o',
    markeredgecolor='black',
    markersize=6,
    markerfacecolor='pink',
)
# 绘制人次折线图
plt.plot(
    wechat.Date,
    wechat.Times,
    '--b*',
)
ax = plt.gca()  # 获取图的坐标信息
date_format = mpl.dates.DateFormatter("%m-%d")
ax.xaxis.set_major_formatter(date_format)
# 设置x轴出现多少个日期刻度(与下面的设置同时实现不了)
# locator = mpl.ticker.LinearLocator(10)
# 设置x轴的刻度隔天次数
locator = mpl.ticker.MultipleLocator(7)
ax.xaxis.set_major_locator(locator)
# 避免x轴的刻度标签紧凑,设置旋转45度
plt.xticks(rotation=45)
plt.xlabel('日期')
plt.ylabel('阅读人数')
plt.legend(['阅读人数', '阅读人次'], ncol=2)
plt.title('每天微信文章阅读人数趋势')
plt.show()
# ————————————————————————————————————___——————————__————__————__————
weather = pd.read_excel(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第6章 Python数据可视化\weather.xlsx')
# 统计每月的平均最高气温
data = weather.pivot_table(
    index='month',  # 行索引
    columns='year',  # 列索引
    values='high'  # 值
)
data.plot(
    kind='line',
    style=['v-b', 'o:r', '*-.g']
)
plt.xlabel('月份')
plt.ylabel('气温')
plt.title('每月的平均气温')
plt.show()

6.面积图

参数	说明	参数	说明

在这里插入代码片

三、关系型数据的可视化

前面两个都是基于独立的离散变量或数值变量进行可视化展示。还有一类用于探究两个或三个之间的变量关系。
如：散点图用于发现两个数值变量之间的关系，气泡图用于展示三个数值变量之间的关系，3.热力图：体现了两个离散变量之间的组合关系。

1.散点图——探究某花花瓣的长度与宽度的关系

下面表格是以matplotlib模块的参数

参数	说明	参数	说明
x	x轴数据	norm	设置数据亮度，0-1，需要参数c为浮点数的数组
y	y轴数据	vmin，vmax	亮度设置，类型norm类似，若使用norm，则该参数无效
s	指定散点图点的大小，通过传入其它值实现气泡图	alpha	设置散点图
c	指定颜色，通过cmap实现色阶表示数值大小	linewidths	设置散点边界线的宽度
marker	形状	edgecolors	设置散点边界线的颜色
cmap	指定某个Colormap值，只有当c参数是一个浮点型数值时才有效

# 散点图
iris = pd.read_csv(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第6章 Python数据可视化\iris.csv')
plt.scatter(
    x=iris.Petal_Width,
    y=iris.Petal_Length,
    color='steelblue',
)
# 添加x、y标签
plt.xlabel('花瓣的宽度')
plt.ylabel('花瓣的长度')
plt.title('花瓣的长度与宽度关系')
plt.show()

下面表格是以seaborn模块的lmplot函数（绘制复杂的散点图使用seabron简单，还可以添加线性拟合）bool指定是参数类型bool类型，后面出现的false或true为默认值

参数	说明	参数	说明
x,y	xy轴数据	fig_reg	bool，是否拟合线性回归，false
data	指定绘图数据集	ci	绘制拟合线的置信区间
hue	指定分组变量	n_boot	为了估计置信区间，指定自助重抽样的次数，默认为1000次
col，row	用于绘制分面图形，指定分面图形的列向与列向变量	order	指定多项式回归，默认指数为1
palette	为hue参数的颜色设置	logistic	是否拟合逻辑回归，false
col_wrap	设置分面图形中每行子图的数量	lowess	bool，是否拟合局部多项式回归，false
size	设置每个分面图形的高度	robust	bool，是否拟合鲁棒回归，false
aspect	设置每个分明图形的宽度，宽度==size*aspect	logx	bool，是否对x轴做对数转换，false
markers	设置点的形状，用于区分hue分组变量	x_partial,y_partial	为x或y轴数据指定控制变量，即排除x,y_partial的变量的影响下绘制散点图
sharex，sharey	bool，设置绘制分面图形时是否共享x，y轴，true	truncate	bool，是否根据实际数据的范围对拟合线做出截断操作，false
hue_ order,col_order,row_order	为hue，col，row参数指定的分组变量设值水平值顺序	x_jitter,y_jitter	为x或y轴随机添加噪声，当x与y轴比较密集时，可以使用这两个参数
legend	bool，是否显示图例 ，true	scatter_kws	设置点的属性，点的填充色、边框色、大小等
legend_out	bool，是否图例放置在图框外,false	line_kws	设置拟合线的属性，如线的形状、颜色、大小等
scatter	bool，是否绘制散点图，true

参数虽然多，但是记住几个重要的，如：x、y、hue、data等

# 使用seaborn做散点图
plt.style.use('ggplot')
plt.rcParams['font.family'] = 'SimHei'
iris = pd.read_csv(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第6章 Python数据可视化\iris.csv')
sns.lmplot(
    x='Petal_Width',
    y='Petal_Length',
    data=iris,
    hue='Species',  # 按照花的品种进行分组
    legend_out=False,
    truncate=True, # 根据实际数据范围对拟合线做截断
    # robust=True
)
plt.xlabel('花瓣的宽度')
plt.ylabel('花瓣的长度')
plt.title('花的花瓣宽度与花瓣长度的关系')
plt.legend(ncol=3)
plt.show()

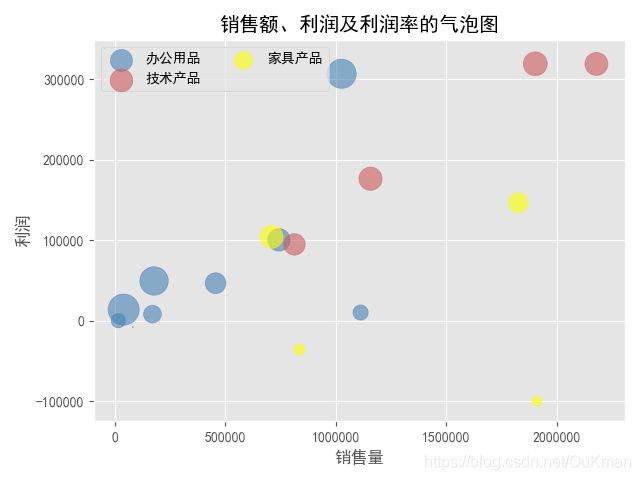
2.气泡图——暴露商品的销售特征

# 绘制气泡图
plt.style.use('ggplot')
plt.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
Prod_Category = pd.read_excel(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第6章 Python数据可视化\SuperMarket.xlsx')
# 将利润率标准化到[0,1]之间（因为利润率中有负数），然后加上微小的数值0.001
range_diff = Prod_Category.Profit_Ratio.max() - Prod_Category.Profit_Ratio.min()
Prod_Category['std_ratio'] = (Prod_Category.Profit_Ratio - Prod_Category.Profit_Ratio.min()) / range_diff + 0.001
# 绘制办公室用品的气泡图
plt.scatter(
    # s<0时点是不显示出来的
    x=Prod_Category.Sales[Prod_Category.Category == '办公用品'],
    y=Prod_Category.Profit[Prod_Category.Category == '办公用品'],
    s=Prod_Category.std_ratio[Prod_Category.Category == '办公用品'] * 500,  # 设置点的大小
    color='steelblue',
    label='办公用品',
    alpha=0.6
)
plt.scatter(
    x=Prod_Category.Sales[Prod_Category.Category == '技术产品'],
    y=Prod_Category.Profit[Prod_Category.Category == '技术产品'],
    s=Prod_Category.std_ratio[Prod_Category.Category == '技术产品'] * 500,  # 设置点的大小
    color='indianred',
    label='技术产品',
    alpha=0.6
)
plt.scatter(
    x=Prod_Category.Sales[Prod_Category.Category == '家具产品'],
    y=Prod_Category.Profit[Prod_Category.Category == '家具产品'],
    s=Prod_Category.std_ratio[Prod_Category.Category == '家具产品'] * 500,  # 设置点的大小
    color='yellow',
    label='家具产品',
    alpha=0.6
)
plt.xlabel('销售量')
plt.ylabel('利润')
plt.legend(ncol=2)
plt.title('销售额、利润及利润率的气泡图')
plt.show()

3.热力图——一份简单的月度日历
也被称为 交叉填充表，可以借助seaborn模块的heatmap函数

参数	说明	参数	说明
data	数据集	linecolor	指定每个边框颜色
vmin，vmax	用于指定图例中的最大值和最小值的显示值	cbar	bool，是否用颜色条做为图例，默认为true
cmap	指定一个colormap对象，填充颜色	cbar_kws	有关颜色条的其它属性描述
center	指定颜色中心值，通过该参数调整热力图的颜色深浅	square	bool，是否使用热力图的每个单元格为正方形，默认为false
annot	指定一个bool或data参数形状一样的数组，如果为true，就在热力图的每个单元上显示数值	xticklabls,yticklabels	指定热力图x，y轴的刻度标签，如果为true，则分别以数据框的变量名和行名称作为刻度标签
fmt	指定单元格中的数据显示格式	mask	用于突出显示某些数据
annot_kws	有关单元格中数值标签的其它属性描述，如颜色、大小等	ax	用于指定子图位置
linewidths	指定每个单元个的边框颜色

下面这串代码让热力图
bottom, top = heatmap.get_ylim()
heatmap.set_ylim(bottom + 0.5, top - 0.5)

plt.style.use('ggplot')
plt.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
Sales = pd.read_excel(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第6章 Python数据可视化\Sales.xlsx')
# 根据交易日期，衍生年份和月份字段
Sales['year'] = Sales.Date.dt.year  # 年
# 使用dt将时间戳进行分割出 year和month
Sales['month'] = Sales.Date.dt.month  # 月
# 统计每年个月分的销售总额
Summary = Sales.pivot_table(
    index='month',   # 行索引为月
    columns='year',  # 列索引为年
    values='Sales',  # 对应的为销售额
    aggfunc=np.sum   # 对数据聚合时进行的函数操作
)
# 绘制热力图
sns.heatmap(
    data=Summary,
    cmap='PuBuGn',
    linewidths=.1,  # 设置每个单元格边框的宽度
    annot=True,  # 显示数值
    fmt='.1e'  # 以科学计算法显示数据
)
plt.title('每年各月各日销售总额热力图')
plt.show()

额外补充 ------- 折线图和柱形图：
标签以 for a, b in zip(x, y):
plt.text(a, b, b, ha=“center”(居中), va=“bottom”(数据上面，top下面))

x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([866, 2335, 5710, 6482, 6120, 1605, 3813, 4428, 4631])
plt.plot(x, y, label="这线图")
plt.bar(x, y, label="柱形图")
for a, b in zip(x, y):
    plt.text(a, b, b, ha="center", va="bottom", fontsize=12)
plt.show()

四、多个图形的合并

推荐使用subplot2grid(shape,loc,rowspan=1,colspan=1)

参数	说明	参数	说明
shape	指定组合图的框架形状，以元组形式	colspan	指定某个子图需要跨几列
loc	指定子图的位置，如第一行第一列（0，0）	rowspan	指定某个子图需要跨几行

# 构造2行3列的组合图框架
plt.subplot2grid(shape=(2, 3), loc=(0, 0))
plt.subplot2grid(shape=(2, 3), loc=(0, 2), rowspan=2)
plt.subplot2grid(shape=(2, 3), loc=(1, 0), colspan=2)
plt.subplot2grid(shape=(2, 3), loc=(0, 1))
plt.show()

Prod_Trade = pd.read_excel(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第6章 Python数据可视化\Prod_Trade.xlsx')
# 衍生出年月
Prod_Trade['year'] = Prod_Trade.Date.dt.year
Prod_Trade['month'] = Prod_Trade.Date.dt.month
# 设置大图框架的长和高
plt.figure(figsize=(12, 6))
# 设置第一个子图
ax1 = plt.subplot2grid(shape=(2, 3), loc=(0, 0))
# 统计2012年各订单等级的数量
Class_Counts = Prod_Trade.Order_Class[Prod_Trade.year == 2012].value_counts()
Class_Percent = Class_Counts / Class_Counts.sum()
print(Class_Percent)
# 设置饼图为原型
ax1.set_aspect(aspect='equal')
# 绘制订单等级饼图
ax1.pie(
    x=Class_Percent.values,
    labels=Class_Percent.index,
    autopct='%.1f%%'
)
ax1.set_title('2012年各等级订单比例')
# 设置第二个子图
ax2 = plt.subplot2grid(shape=(2, 3), loc=(0, 1))
# 统计2012年每月的销售额
Month_Sales = Prod_Trade[Prod_Trade.year == 2012].groupby(by='month').aggregate({
    'Sales': np.sum
})
# 绘制销售额趋势图
Month_Sales.plot(
    title='2012年各月的销售趋势',
    ax=ax2,  # 指定子图位置
    legend=False
)
ax2.set_xlabel('')  # 删除x轴标签
# 设置第三个子图
ax3 = plt.subplot2grid(shape=(2, 3), loc=(0, 2), rowspan=2)
sns.boxplot(
    data=Prod_Trade,
    x='Transport',
    y='Trans_Cost',
    ax=ax3,
)
ax3.set_title('各运输方式的成本')
ax3.set_xlabel('')
ax3.set_ylabel('运输成本')
# 设置第四个子图
ax4 = plt.subplot2grid(shape=(2, 3), loc=(1, 0), colspan=2)
# 2012各单价分布直方图
sns.distplot(
    Prod_Trade.Sales[Prod_Trade.year == 2012], bins=40, norm_hist=True,
    ax=ax4,
    hist_kws={
        'color': 'steelblue',
    },
    kde_kws={
        'linestyle': '--',
        'color': 'indianred'
    }
)
ax4.set_title('22012年客单价分布图')
ax4.set_xlabel('销售额')
# 调节子图之间的水平和高度间距
plt.subplots_adjust(hspace=0.6,wspace=0.3)
plt.show()

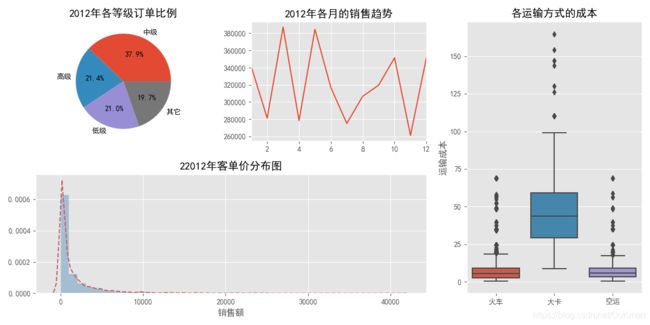
从上面代码需要注意的几个点：
1.使用每个子图前使用subplot2grid函数控制子图位置
2.使用matplotlib模块则指定子图时如ax1.plot_function的代码语法，若是pandas或seaborn则使用ax参数
3.若为子图添加标题、坐标轴标签、刻度值等时需要ax1.set_的形式，而不能直接plt.
4.可以通过subplots_adjust控制子图之间的间隔

线性回归预测模型

一、一元线性回归模型—————————

应用场景：（适用用于一个因变量和一个自变量）
1.餐厅根据每天的营业数据预测就餐规模或营业额
2.网站根据访问量的历史记录预测用户的支付转换率
3.医院根据患者的病例数据预测某种疾病发生的概率
用到的模块是 statsmodels.api 的 ols函数

函数	使用\参数
ols	formula：以字符串形式指定线性回归模型的公式，如‘x~y’
ols	data: 指定建模的数据集
ols	subset，bool类型参数，获取data的子集用于建模
ols	drop_cols:指定从data中删除变量
sm.formula.ols(‘参数1’ ~ ‘参数2’，data=’'数据源) .fit()（要加）	返回 fit.params 可以自己索引[a,b]

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm

# 使用普通做法
# 读取数据
income = pd.read_csv(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第7章 线性回归模型\Salary_Data.csv')
# 绘制散点图
sns.lmplot(
    data=income,
    x='YearsExperience',
    y='Salary',
    ci=None,
    scatter_kws={
        'color': 'indianred',
    }

)
plt.show()

# 一、拟合线的求解(徒手算)
# 样本量
n = income.shape[0]  # 返回行数
r = income.shape[1]  # 返回列数
# 计算自变量，因变量，自变量平方，自变量与因变量乘积的合
sum_x = income.YearsExperience.sum()  # 年经验的总和
sum_y = income.Salary.sum()  # 工资的总和
sum_x2 = income.YearsExperience.pow(2).sum()  # 幂运算
xy = income.YearsExperience * income.Salary  # 年经验*工资
sum_xy = xy.sum()  # 年经验*工资的总和
# 根据公式计算回归模型的参数
b = (sum_xy - sum_x * sum_y / n) / (sum_x2 - sum_x ** 2 / n)  # b=(年经验*工资的总和 - 年经验的总和*工资的总和/行数)/(各工资的平方的总和-总工资的平方/行数)
a = income.Salary.mean() - b * income.YearsExperience.mean()  # a=工资的平均数 - b*年经验的平均数

print('回归参数a的值', a)
print('回归参数b的值', b)
# -----------------------------
# 使用模块statsmodels进行计算
# 利用收入数据集，构建回归模型(操作方便)
fit = sm.formula.ols(
    'Salary ~ YearsExperience', data=income
).fit()
var = fit.params
print('回归参数a的值', var[0], '回归参数b的值', var[1])
'''
关于收入的线性回归模型可以表示:
 Salary = 25792.20 + 9449.96YearsExperience
'''

二、多元线性回归模型——销售利润预测

适用于多个自变量
使用的模块为
1.from sklearn import model_selection
2.import statsmodles.api
3.还用到了设置哑变量效果：ols的C()方法，但是不可以自己指定变量中的某个值作为对照组，所以使用pandas.get_dummies()

实现回归模型的预测使用predict方法predict(exog=none,transform=true)

参数	说明	参数	说明
exog	指定用于预测的其他自变量的值	transform	bool类型参数，预测时是否将原始数据按照模型表达式进行转换，默认为True

from sklearn import model_selection
import pandas as pd
import statsmodels.api as sm

Profit = pd.read_excel(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第7章 线性回归模型\Predict to Profit.xlsx')

# 将数据集拆分为训练集和测试集
train, test = model_selection.train_test_split(Profit, test_size=0.2, random_state=1234)
# 根据train数据集建模
model = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + C(State)'
                       , data=train).fit()

print('模型的偏回归系数分别为：\n', model.params)

# 删除test数据集中的Profit变量，用剩下的自变量进行预测
test_x = test.drop(labels='Profit', axis=1)
pred = model.predict(exog=test_x)
print(
    '对比预测值和实际值的差异: \n', pd.DataFrame({'Prediction': pred,'Real': test.Profit})
)


# ——————————————————————
# 生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
# 将沙哑变量与原始数据集水平合并
Profit_New = pd.concat([Profit, dummies], axis=1)
# 删除State 变量和 California变量（因为State变量已被分解为哑变量，New York 变量需要作为参照组）
Profit_New.drop(labels=['State', 'New York'], axis=1, inplace=True)
# 拆分数据集Profit_New
train, test = model_selection.train_test_split(Profit_New, test_size=0.2, random_state=1234)
# 建模
mode12 = sm.formula.ols('Profit ~ RD_Spend+Administration + Marketing_Spend+Florida+California', data=train).fit()
print('模型的偏回归系数分别为:\n', mode12.params)
'''
从离散变量State中衍生出来的哑变量在回归系数的结果只保留了Florida和California，而New York变量则作为了参照组
公式：
   Profit=58068.05+0.80*RD_Spend -0.06*Administration+0.01*Marketing_Spend+1440.86*Florida+513.47*California
'''

三、回归模型的假设检验

上面关于产品的利润的多元线性回归模型已经构建完成，但是该模型的好与坏还没有相应的结论，还需进行模型的显著性检验和回归系数的显著性检验（分别使用了统计学的F检验法和t检验法）。
具体的检验步骤：
1.提出问题的原假设和备假设
2.在原假设的条件下，构造统计量F
3.根据样本信息，计算统计量的值
4.对比统计量的值和理论F分布的值，如果计算的统计量值超过理论的值，则拒绝原假设，否则需要受原假设

1.显著性检验-F检验法

# 代码已经是第三步骤：计算统计量
import numpy as np
import pandas as pd
import statsmodels.api as sm
from sklearn import model_selection

Profit = pd.read_excel(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第7章 线性回归模型\Predict to Profit.xlsx')
# 生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
# 将沙哑变量与原始数据集水平合并
Profit_New = pd.concat([Profit, dummies], axis=1)
# 删除State 变量和 California变量（因为State变量已被分解为哑变量，New York 变量需要作为参照组）
Profit_New.drop(labels=['State', 'New York'], axis=1, inplace=True)
# 拆分数据集Profit_New
train, test = model_selection.train_test_split(Profit_New, test_size=0.2, random_state=1234)
# 建模
mode12 = sm.formula.ols('Profit ~ RD_Spend+Administration + Marketing_Spend+Florida+California', data=train).fit()
# 计算建模数据中因变量的均值
ybar = train.Profit.mean()
# 统计变量个数和观测个数
p = mode12.df_model
n = train.shape[0]  # 行个数
print(n)
# 计算回归离差平方和
RSS = np.sum((mode12.fittedvalues - ybar) ** 2)
# 计算误差平方和
ESS = np.sum(mode12.resid ** 2)
# 计算F统计变量的值
F = (RSS / p) / (ESS / (n - p - 1))
print('F统计量的值：', F)

2.t检验

# 同样的4步骤：为了方便起见直接使用summary()
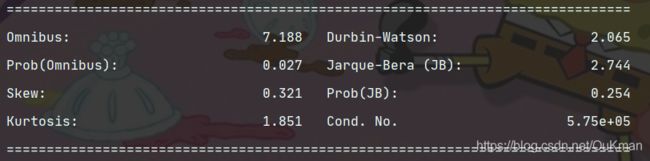
print(mode12.summary())

四、回归模型的诊断

回归建模构建好之后，还需要进一步的进行诊断，目的是使得建模更加健壮，主要针对几个假设：
1.误差项E服从正态分布
2.无多重共线性
3.线性相关性
4.误差项E得独立性
5.方差齐性
除了上面5点以外，还需注意线性回归模型对异常值是非常敏感的，模型构建过程非常受异常值的影响。
注意一个语法： Profit_New.ix[:, [‘RD_Spend’, ‘Administration’, ‘Marketing_Spend’, ‘Profit’]]的：是来指定所有行
1.正态性检验

1.1直方图法

import scipy.stats as states
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import statsmodels.api as sm
from sklearn import model_selection

Profit = pd.read_excel(r'D:\大学\大二第一学期\python3资料\数据挖掘资料\《从零开始学Py   源代码\第7章 线性回归模型\Predict to Profit.xlsx')
# 生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
# 将沙哑变量与原始数据集水平合并
Profit_New = pd.concat([Profit, dummies], axis=1)
# 删除State 变量和 California变量（因为State变量已被分解为哑变量，New York 变量需要作为参照组）
Profit_New.drop(labels=['State', 'New York'], axis=1, inplace=True)
# 拆分数据集Profit_New
train, test = model_selection.train_test_split(Profit_New, test_size=0.2, random_state=1234)
# 建模
mode12 = sm.formula.ols('Profit ~ RD_Spend+Administration + Marketing_Spend+Florida+California', data=train).fit()

# 1.直方图法
plt.rcParams['font.family'] = 'Microsoft YaHei'
plt.rcParams['axes.unicode_minus'] = False

sns.distplot(
    a=Profit_New.Profit,
    bins=10,
    fit=states.norm,
    norm_hist=True,
    hist_kws={
        'color': 'steelblue',
        'edgecolor': 'black'
    },
    kde_kws={
        'color': 'black',
        'linestyle': '--',
        'label': '核密度曲线'
    },
    fit_kws={
        'color': 'red',
        'linestyle': ':',
        'label': '正态密度曲线'
    }
)
plt.legend()
plt.show()
'''
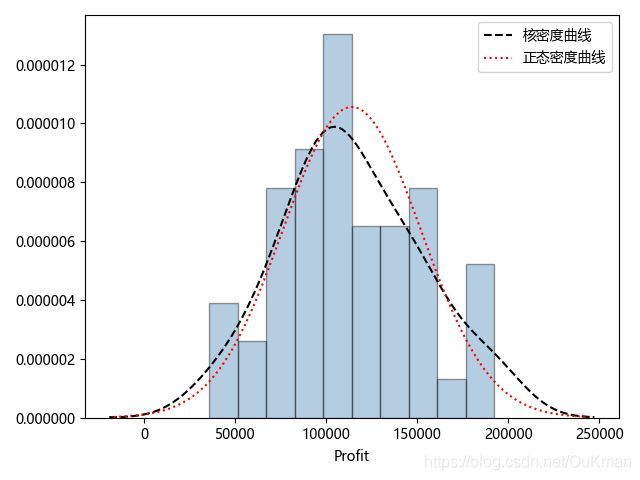
因变量Profit的直方图、核密度曲线、理论正态分布的密度曲线
添加两个曲线的目的是为了对比数据的实际分布和理论分布之间的差异。
如果两条曲线近似或吻合就说明此变量近似服从正态分布（该图就是）。
故直观上可以认为利润变量服从正态分布
'''

1.2 PP图和QQ图

# 1.2 PP图和QQ图
plt.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
ax1 = plt.subplot2grid(shape=(1, 2), loc=(0, 0))
ax2 = plt.subplot2grid(shape=(1, 2), loc=(0, 1))
# 残差的正态性检验（PP图和QQ图法）
pp_qq_plot = sm.ProbPlot(Profit_New.Profit)
# 绘制pp图
pp_qq_plot.ppplot(
    line='45',
    ax=ax1
)
ax1.set_title('p-p图')
# 绘制qq图
pp_qq_plot.qqplot(
    line='q',
    ax=ax2
)
ax2.set_title('Q-Q图')
plt.show()
'''
PP图：比对正态分布的累计概率值和实际分布的累计概率值。
QQ图：比对正态分布的分位数和实际分布的分位数。
判断变量是否近似服从正态分布的标准是：
如果散点都比较均匀地散落在直线上，证明变量近似服从正态分布，否则反之
不管是qq图还是pp图散点均匀落在直线附近，故认为利润变量近似服从正态分布
'''

1.3 shapiro 检验和K-S检验
这两种方法均属于非参数方法，它们的原假设被设定为变量服从正态分布，两者的区别在于shapiro适用于数据量定于5000合理，而K-S检验反之，。 scipy的子模块stats提供了专门的检验函数shapior和kstest

# 1.3 shapiro检验（因为数据量小于5000）
# Shapiro检验
print(states.shapiro(Profit_New.Profit))  # 元组的第一个元素是shapiro检验的统计量值，第二个元素是对应的概率值p
'''
因为p值大于置信水平0.05，故接受利润变量服从正态分布的假设
'''

# 应用kstest函数
# 生成正态分布和均匀分布随机数（模拟数据）
rnorm = np.random.normal(loc=5, scale=2, size=10000)
runif = np.random.uniform(low=1, high=100, size=10000)
# 正态分布检验
KS_Test1 = states.kstest(rvs=rnorm, args=(rnorm.mean(), rnorm.std()), cdf='norm')
KS_Test2 = states.kstest(rvs=runif, args=(runif.mean(), runif.std()), cdf='norm')
print(KS_Test1)
print(KS_Test2)
'''
p值大与水平0.05，则需接受原假设；
均匀分布随机数的检验p值远远小于0.05，则需拒接原假设
如果使用kstest函数对变量进行正态性检验，必须指定args参数，它用于传递被检验变量的均值和标准差
如果因变量检验结果不满足正态分布时，需要对因变量做某种属性转换，使用比较多的是方法是：
   log(y)，根号y、根号y分之一，y**2，1/y**2等
'''

2.多重共线性检验

是指模型中的自变量之间存在较高的线性相关关系，它对模型带来严重后果，例如：“最小二乘法”得到懂得偏回归系数无效、增大偏回归系数的方差、模型缺乏稳定性等。可以使用方差膨胀因子VIF鉴定，
VIF>10 ：存在多重共线性问题，VIP>100：变量间存在严重的多重共线问题
使用statsmodels模块中的函数

from statsmodels.stats.outliers_influence import variance_inflation_factor

# 自变量X（包含RD_Spend\Marketing_Spend和常数列1）
X = sm.add_constant(Profit_New.ix[:, ['RD_Spend', 'Marketing_Spend']])
# 使用构造空的数据框，用于存储VIF值
vif = pd.DataFrame()
vif["features"] = X.columns
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
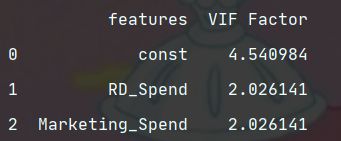
print(vif)
'''
两个自变量对应的方差膨胀因子均低于10，说明构造模型的数据并不存在多重共线性。
如果存在多的话可以考虑删除变量或者重新建模（如岭回归模型或LASSO模型）
'''

3.线性相关性检验
用于确保建模的自变量和因变量之间存在的线性关系。可以用Pearson相关系数和可视化方法进行识别，直接使用数据框的方法corrwith，该方法最大的好处是可以计算任意指定变量间的相关系数。

线性相关的程度说明:p都有绝对值符号

p >=0.8	0.5=	0.=	p<0.3
高度相关	中度相关	弱相关	几乎不相关

# 3 线性相关性检验
# 计算数据集Profit_New中每个自变量和因变量利润之间的相关系数
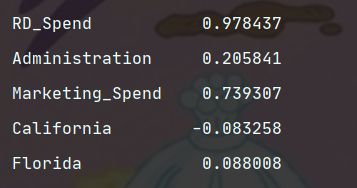
x = Profit_New.drop('Profit', axis=1).corrwith(Profit_New.Profit)
print(x)
'''
线性关系强的有RD_Spend    0.978437
Marketing_Spend    0.739307
其它基本没有线性相关
'''
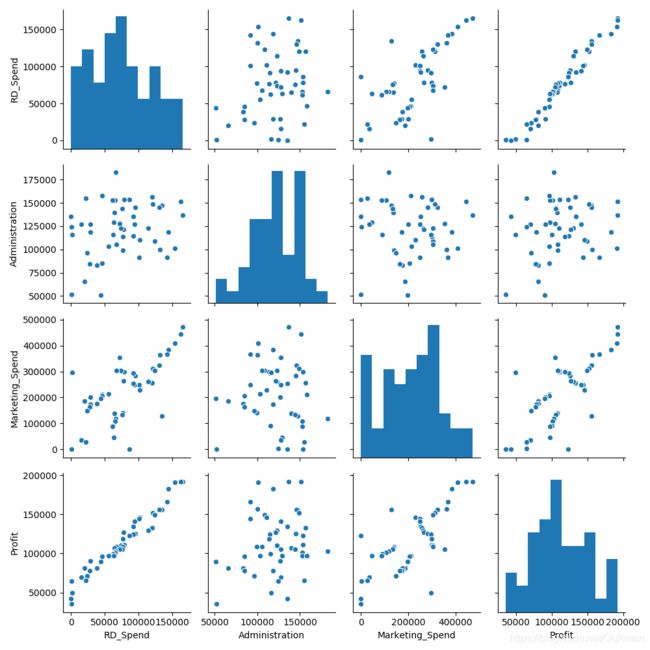
# 绘制散点图矩阵
sns.pairplot(
    # : 代表所有行
    Profit_New.ix[:, ['RD_Spend', 'Administration', 'Marketing_Spend', 'Profit']]
    # 因为California  Florida是哑变量故没有放入散点图中
)
plt.show()
'''
从图可以分析：
  （左下角）研发成本和利润之间的散点图几乎为一条向上直线：说明两种变量存在很强的线性关系
  （第一列第二行）管理成本和利润之间呈水平的趋势且宽，证明两种确实没有任何关系
'''
# 总和考虑相关系数，散点图矩阵，和t检验的结果，修正模型，只保留线性相关的变量RD_Spend,Marketing_Spend
mode13 = sm.formula.ols('Profit ~ RD_Spend+Marketing_Spend', data=train).fit()
print(mode13.params)  # 返回的模型是两个自变量的系数估计值
'''
可以将多元线性规划模型表示成：Profit=51902.112471+0.79RD_Spend+0.02Marketing_Spend
'''

4.异常值检验
多元线性回归模型容易受到极端值的影响，故需要异常值检验，对其进行数据整改、如删除异常值或衍生出是否为异常值的哑变量。
主要方法有四种：
1.帽子矩阵
2.DFFITS准则
3.学生化残差
4.Cook距离

# 异常值检验
outliers = mode13.get_influence()
# 高杠杆值点（帽子矩阵）
leverage = outliers.hat_matrix_diag
# dffits值
dffits = outliers.dffits[0]
# 学生化残差
resid_stu = outliers.resid_studentized_external
# cook距离
cook = outliers.cooks_distance[0]
# 合并各种异常值检验的统计量值
contata1 = pd.concat([pd.Series(leverage, name='leverage'),
                      pd.Series(dffits, name='dffits'),
                      pd.Series(resid_stu, name='resid_stu'),
                      pd.Series(cook, name='cook')], axis=1)
# 重设train数据的行索引
train.index = range(train.shape[0])
# 将上面的统计量与train据集合并起来
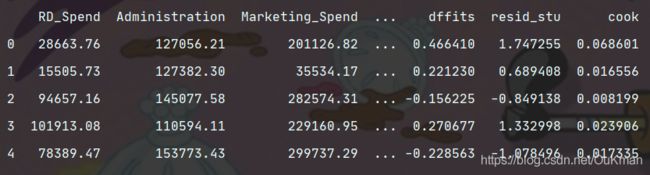
profit_outliers = pd.concat([train, contata1], axis=1)
print(profit_outliers.head(5))
# 计算异常值数量的比例
outliers_ratio = sum(np.where((np.abs(profit_outliers.resid_stu) > 2), 1, 0)) / profit_outliers.shape[0]
print(outliers_ratio)
'''
得知异常比例为2.5%。对异常值处理的两种方法： 
1.异常值比例（低于=5%）：可以考虑删除
2.异常值比例高（可能删除一些重要信息）：需要衍生哑变量，对异常点设置哑变量的值为1，否则为0
'''
# 删除异常值
# 挑选出非异常值的观测点
none_outliers = profit_outliers.ix[np.abs(profit_outliers.resid_stu) <= 2,]
# 应用无异常值得数据集重新建模
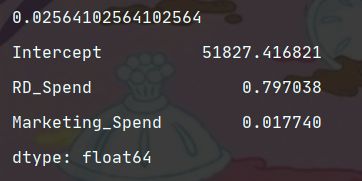
mode14 = sm.formula.ols('Profit~RD_Spend+Marketing_Spend', data=none_outliers).fit()
print(mode14.params)
# 经过异常点得排除重新构建偏回归系数发生了变动：Profit= 51827.416821+0.80RD_Spend+0.02Marketing_Spend

5.独立性检验
对因变量y得独立性检验，因为线性回归模型得等式左右只有y和残差项E属于随机变量，如果再加上正态分布，就构成了残差项独立同分布于正态分布得假设。独立性检验通常使用Durbin-Waston统计量值来参数，DW值在2左右，编码残差项之间是不相关得；如果偏离2较远，说明不满足残差得独立性假设。不需要格外计算，一位已经在summary()里面了。

# 由结果可知DW统计值为2.065，比较接近2，故认为模型得残差项之间是满足独立性这个假设前提得
print(mode14.summary())

6.方差齐性检验
方差齐性要求模型残差项得方差不随自变量得变动而呈现某种趋势，否则，残差得趋势就可以被自变量刻画。如果残差项不满足方差齐性，就会导致偏回归系数不具备有效性，可能导致建模得预测也不正确。一般有两种方法：
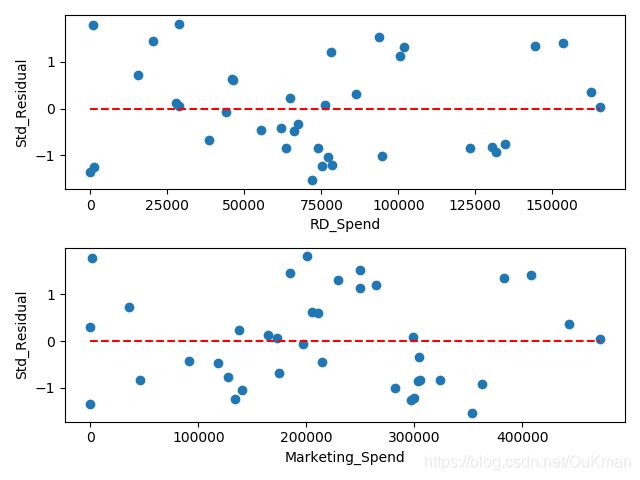
1.图形法（散点图）

# 1.图形法
# 设置第一张子图的位置
ax1 = plt.subplot2grid(shape=(2, 1), loc=(0, 0))
# 绘制散点图
ax1.scatter(
    none_outliers.RD_Spend,
    (mode14.resid - mode14.resid.mean()) / mode14.resid.std()
)
# 添加水平参考线
ax1.hlines(
    y=0,
    xmin=none_outliers.RD_Spend.min(),
    xmax=none_outliers.RD_Spend.max(),
    colors='red',
    linestyles='--'
)
# 添加x轴和y轴标签
ax1.set_xlabel('RD_Spend')
ax1.set_ylabel('Std_Residual')
# 设置第二张子图的位置
ax2 = plt.subplot2grid(shape=(2, 1), loc=(1, 0))
ax2.scatter(
    none_outliers.Marketing_Spend,
    (mode14.resid - mode14.resid.mean()) / mode14.resid.std()
)
ax2.hlines(
    y=0,
    xmin=none_outliers.Marketing_Spend.min(),
    xmax=none_outliers.Marketing_Spend.max(),
    colors='red',
    linestyles='--'
)
ax2.set_xlabel('Marketing_Spend')
ax2.set_ylabel('Std_Residual')
# 调整子图之间的位置
plt.subplots_adjust(hspace=0.6, wspace=0.3)
plt.show()
'''
从图可以看出:
标准化残差并没有随自变量的变动而呈现喇叭形
所有的散点几乎均匀地分布在参考线y=0的附近
说明模型的残差项满足方差齐性的前提假设
'''

2.统计检验法（BP检验）
假设是残差是一个参数，通过构造拉格朗日乘子LM统计量，实现方差齐性的检验。借助statsmodels模块中的het_breushpagan的函数

print(sm.stats.diagnostic.het_breuschpagan(mode14.resid, exog_het=mode14.model.exog))
'''
如下结果：
(1.467510366830809,  ——LM统计量
 0.48010272699006995,  ——是统计量的对应概率p值，大与0.05说明残差方差为产生的原假设
 0.7029751237162342,  ——F统计量，检验残差平方项于自变量之间是否独立，独立则表明残差方差差齐性
 0.5019659740962923)  ——是F统计变量的概率p值，同样大与0.05，则进一步表满残差项满足方差齐性的假设
'''

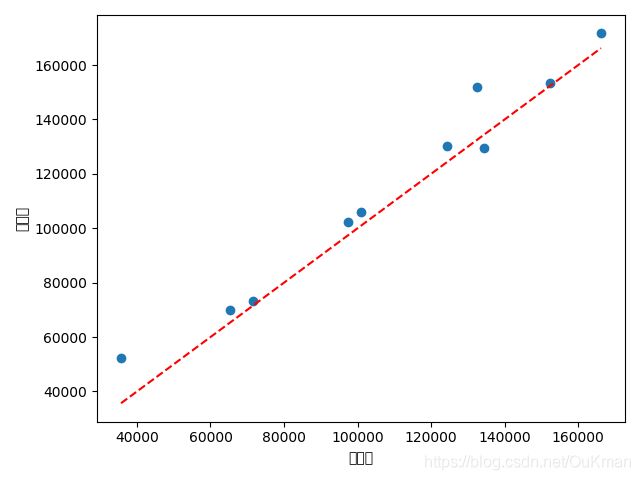
7.回归模型的预测

# 对mode14对测试集的预测
pred4 = mode14.predict(exog=test.ix[:, ['RD_Spend',
                                        'Marketing_Spend']])
# 绘制预测值与实际值的散点图
plt.scatter(
    x=test.Profit,
    y=pred4
)
# 添加斜率为1，截距项为0的参考线
plt.plot(
    [test.Profit.min(), test.Profit.max()],
    [test.Profit.min(), test.Profit.max()],
    color='red',
    linestyle='--'
)
plt.xlabel('实际值')
plt.ylabel('预测值')
plt.show()
'''
由图可知大部分的散点在对角线附近，证明模型预期效果还是不错的
'''

忘记设置中文许可

线性回归模型的函数和‘方法’总结

Python模块	Python函数或方法	函数说明
statsmodels	ols	构建线性回归模型的函数
statsmodels	fit	基于模型的参数拟合”方法“
statsmodels	predict	基于模型的预测”方法“
statsmodels	params	返回模型的回归系数
statsmodels	fvalue	返回模型显著检验的f值
statsmodels	tvalue	返回回归系数显著性检验的t值
statsmodels	summary	返回模型概览信息的方法
statsmodels	ppplot	绘制pp图的函数
statsmodels	qqplot	绘制qq图的函数
statsmodels	variance_inflation_factor	计算方差膨胀因子的函数
statsmodels	get_influence	基于模型的异常值获取”方法“
statsmodels	hat_matrix_diag	返回帽子矩阵的对角线元素
statsmodels	diffits	返回DFFITS准则的统计量
statsmodels	resid_studentized_external	返回标准化残差的统计量
statsmodels	cooks_distance	返回Cook距离的统计量
statsmodels	het_breushpagan	用于检验误差方差差齐性的函数
scipy	kstest	K-S正态性检验函数
scipy	shapiro	Shapiro正态性检验函数
scipy	ppf	计算F分布分位点的函数
pandas	corrwith	计算呢Perason相关系数的“方法”
sklearn	train_test_split	用于分割训练集和测试集的函数