DoubleDQN的理论基础及其代码实现【Pytorch + Pendulum-v0】

Double DQN 理论基础

普通的 DQN 算法通常会导致对值的过高估计（overestimation）。传统 DQN 优化的 TD 误差目标为
$r+\gamma {\max }_{a^{\prime }}{Q}_{{\omega }^{-}}\left(s^{\prime },a^{\prime }\right)$
其中${\max }_{a^{\prime }}{Q}_{{\omega }^{-}}\left(s^{\prime },a^{\prime }\right)$由目标网络（参数为$w^{-}$）计算得出，我们还可以将其写成如下形式：
$Q_{{\omega }^{-}}\left(s^{\prime },\arg {\max }_{a^{\prime }}{Q}_{{\omega }^{-}}\left(s^{\prime },a^{\prime }\right)\right)$

换句话说，$\max$操作实际可以被拆解为两部分：

• 首先选取状态$s^{\prime }$下的最优动作$a^{\ast }=\arg {\max }_{a^{\prime }}{Q}_{{\omega }^{-}}\left(s^{\prime },a^{\prime }\right)$
• 接着计算该动作对应的价值$Q_{{\omega }^{-}}\left(s^{\prime },a^{\ast }\right)$

当这两部分采用同一套Q网络进行计算时，每次得到的都是神经网络当前估算的所有动作价值中的最大值。考虑到通过神经网络估算的Q值本身在某些时候会产生正向或负向的误差，在 DQN 的更新方式下神经网络会将正向误差累积。
例如，我们考虑一个特殊情形：在状态$s^{\prime }$下所有动作的值均为 0，即$Q\left(s^{\prime },a_i\right)=0,\forall i$，此时正确的更新目标应为$r+0=r$，但是由于神经网络拟合的误差通常会出现某些动作的估算有正误差的情况，即存在某个动作$a^{\prime }$有$Q\left(s^{\prime },a^{\prime }\right)>0$，此时我们的更新目标出现了过高估计，$r+\gamma \max Q>r+0$。因此，当我们用 DQN 的更新公式进行更新时，$Q(s,a)$也就会被过高估计了。同理，我们拿这个$Q(s,a)$来作为更新目标来更新上一步的Q值时，同样会过高估计，这样的误差将会逐步累积。对于动作空间较大的任务，DQN 中的过高估计问题会非常严重，造成 DQN 无法有效工作的后果。

为了解决这一问题，Double DQN 算法提出利用两个独立训练的神经网络估算${\max }_{a^{\prime }}{Q}_{\ast }\left(s^{\prime },a^{\prime }\right)$。具体做法是将原有的${\max }_{a^{\prime }}{Q}_{{\omega }^{-}}\left(s^{\prime },a^{\prime }\right)$更改为$Q_{{\omega }^{-}}\left(s^{\prime },\arg {\max }_{a^{\prime }}{Q}_{\omega }\left(s^{\prime },a^{\prime }\right)\right)$，即利用一套神经网络$Q_w$的输出选取价值最大的动作，但在使用该动作的价值时，用另一套神经网络$Q_w^{-}$计算该动作的价值。这样，即使其中一套神经网络的某个动作存在比较严重的过高估计问题，由于另一套神经网络的存在，这个动作最终使用的Q值不会存在很大的过高估计问题。

传统的 DQN 算法中，本来就存在两套Q函数的神经网络——目标网络和训练网络，只不过${\max }_{a^{\prime }}{Q}_{{\omega }^{-}}\left(s^{\prime },a^{\prime }\right)$的计算只用到了其中的目标网络，那么我们恰好可以直接将训练网络作为 Double DQN 算法中的第一套神经网络来选取动作，将目标网络作为第二套神经网络计算值，这便是 Double DQN 的主要思想。由于在 DQN 算法中将训练网络的参数记为$w$，将目标网络的参数记为$w^{-}$，因此，我们可以直接写出如下 Double DQN 的优化目标：
$r+\gamma Q_{{\omega }^{-}}\left(s^{\prime },\underset{a^{\prime }}{\mathrm{argmax}}{Q}_{\omega }\left(s^{\prime },a^{\prime }\right)\right)$

Double DQN 代码实现

总的来说，DQN 与 Double DQN 的差别只是在于计算状态$s^{\prime }$下Q值时如何选取动作：

• DQN 的优化目标可以写为$r+\gamma Q_{{\omega }^{-}}\left(s^{\prime },\arg {\max }_{a^{\prime }}{Q}_{{\omega }^{-}}\left(s^{\prime },a^{\prime }\right)\right)$，动作的选取依靠目标网络$Q_{w^{-}}$；
• Double DQN 的优化目标为$r+\gamma Q_{{\omega }^{-}}\left(s^{\prime },\arg {\max }_{a^{\prime }}{Q}_{\omega }\left(s^{\prime },a^{\prime }\right)\right)$，动作的选取依靠训练网络$Q_w$。

所以 Double DQN 的代码实现可以直接在 DQN 的基础上进行，无须做过多修改。

Pendulum环境介绍

本次使用的环境是倒立摆（Inverted Pendulum），该环境下有一个处于随机位置的倒立摆。环境的状态包括倒立摆角度的正弦值$\sin \theta$，余弦值$\cos \theta$，角速度$\dot{\theta }$；动作为对倒立摆施加的力矩。每一步都会根据当前倒立摆的状态的好坏给予智能体不同的奖励，该环境的奖励函数为$-\left({\theta }^2+0.1{\dot{\theta }}^2+0.001a^2\right)$，倒立摆向上保持直立不动时奖励为 0，倒立摆在其他位置时奖励为负数。环境本身没有终止状态，运行 200 步后游戏自动结束。

Pendulum环境的状态空间

标号	名称	最小值	最大值
0	$\cos \theta$	-1.0	1.0
1	$\sin \theta$	-1.0	1.0
2	$\dot{\theta }$	-8.0	8.0

Pendulum环境的动作空间

标号	动作	最小值	最大值
0	力矩	-2.0	2.0

力矩大小是在范围内的连续值。由于 DQN 只能处理离散动作环境，因此我们无法直接用 DQN 来处理倒立摆环境，但倒立摆环境可以比较方便地验证 DQN 对Q值的过高估计****：倒立摆环境下值的最大估计应为 0（倒立摆向上保持直立时能选取的最大值），值出现大于 0 的情况则说明出现了过高估计。为了能够应用 DQN，我们采用离散化动作的技巧。例如，下面的代码将连续的动作空间离散为 11 个动作。动作分别代表$[0,1,2,\dots ,9,10]$，力矩为$[-2,-1.6,-1.2,\dots ,1.2,1.6,2]$。

Double DQN 代码实现

在 DQN 代码的基础上稍做修改就可实现 Double DQN。

class DQN:
    def __init__(self, args):
        self.args = args
        self.hidden_dim = 128
        self.batch_size = args.batch_size
        self.lr = args.lr
        self.gamma = args.gamma  # 折扣因子
        self.epsilon = args.epsilon  # epsilon-贪婪策略
        self.target_update = args.target_update  # 目标网络更新频率
        self.count = 0  # 计数器,记录更新次数
        self.num_episodes = args.num_episodes
        self.minimal_size = args.minimal_size
        self.dqn_type = args.dqn_type

        self.env = gym.make(args.env_name)

        random.seed(args.seed)
        np.random.seed(args.seed)
        self.env.seed(args.seed)
        torch.manual_seed(args.seed)

        self.replay_buffer = ReplayBuffer(args.buffer_size)

        self.state_dim = self.env.observation_space.shape[0]
        self.action_dim = 11  # 将连续动作分成11个离散动作

        self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

        self.q_net = Qnet(self.state_dim, self.hidden_dim, self.action_dim).to(self.device)
        self.target_q_net = Qnet(self.state_dim, self.hidden_dim, self.action_dim).to(self.device)

        self.optimizer = Adam(self.q_net.parameters(), lr=self.lr)

    def select_action(self, state):  # epsilon-贪婪策略采取动作
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.action_dim)
        else:
            state = torch.tensor([state], dtype=torch.float).to(self.device)
            action = self.q_net(state).argmax().item()
        return action

    def max_q_value(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        return self.q_net(state).argmax().item()

    def update(self, transition):
        states = torch.tensor(transition["states"], dtype=torch.float).to(self.device)
        actions = torch.tensor(transition["actions"]).view(-1, 1).to(self.device)
        rewards = torch.tensor(transition["rewards"], dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition["next_states"], dtype=torch.float).to(self.device)
        dones = torch.tensor(transition["dones"], dtype=torch.float).view(-1, 1).to(self.device)

        q_values = self.q_net(states).gather(1, actions)  # Q value

        # 下个状态的最大Q值
        ##################################################################
        if self.dqn_type == 'DoubleDQN':
            max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
            max_next_q_values = self.target_q_net(next_states).gather(1, max_action)
        else:  # DQN
            max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)
        ##################################################################

        q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)  # TD error

        loss = torch.mean(F.mse_loss(q_values, q_targets))  # 均方误差损失函数
        self.optimizer.zero_grad()  # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
        loss.backward()  # 反向传播更新参数
        self.optimizer.step()

        if self.count % self.target_update == 0:
            self.target_q_net.load_state_dict(self.q_net.state_dict())  # 更新目标网络

        self.count += 1

只在update()函数里面有所更改，注意看Double DQN的实现方式。另外，max_q_value()函数是为了后面验证过高估计使用的。

def dis_to_con(discrete_action, env, action_dim):
    """离散动作转回连续的函数"""
    action_lowbound = env.action_space.low[0]  # 连续动作的最小值
    action_upbound = env.action_space.high[0]  # 连续动作的最大值
    return action_lowbound + (discrete_action / (action_dim - 1)) * (action_upbound - action_lowbound)

DQN与Double DQN的训练结果对比

接下来我们对比一下 DQN 和 Double DQN 的训练情况，为了便于后续多次调用，我们进一步将 DQN 算法的训练过程定义成一个函数。训练过程会记录下每个状态的最大Q值，在训练完成后我们可以将结果可视化，观测这些Q值存在的过高估计的情况，以此来对比 DQN 和 Double DQN 的不同。

def train_DQN(self):
    return_list = []
    max_q_value_list = []
    max_q_value = 0
    for i in range(10):
        with tqdm(total=int(self.num_episodes / 10), desc=f'Iteration {i}') as pbar:
            for episode in range(self.num_episodes // 10):
                episode_return = 0
                state = self.env.reset()
                while True:
                    action = self.select_action(state)
                    max_q_value = self.max_q_value(state) * 0.005 + max_q_value * 0.995  # 平滑处理
                    max_q_value_list.append(max_q_value)  # 保存每个状态的最大Q值

                    action_continuous = dis_to_con(action, self.env, self.action_dim)
                    next_state, reward, done, _ = self.env.step([action_continuous])

                    self.replay_buffer.add(state, action, reward, next_state, done)

                    if self.replay_buffer.size() > self.minimal_size:
                        s, a, r, s_, d = self.replay_buffer.sample(self.batch_size)
                        transitions = {"states": s, "actions": a, "rewards": r, "next_states": s_, "dones": d}
                        self.update(transitions)

                    state = next_state
                    episode_return += reward

                    if done: break

                return_list.append(episode_return)
                if (episode + 1) % 10 == 0:
                    pbar.set_postfix(
                        {
                            "episode": f"{self.num_episodes / 10 * i + episode + 1}",
                            "return": f"{np.mean(return_list[-10:]):3f}"
                        }
                    )
                pbar.update(1)
    return return_list, max_q_value_list

首先训练 DQN 并打印出其学习过程中最大Q值的情况。

args = define_args()
model = DQN(args)
return_list, max_q_value_list = model.train_DQN()

episodes_list = list(range(len(return_list)))
mv_return = utils.moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(args.env_name))
plt.show()

frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('DQN on {}'.format(args.env_name))
plt.show()

根据代码运行结果我们可以发现，DQN 算法在倒立摆环境中能取得不错的回报，最后的期望回报在-200 左右，但是不少Q值超过了 0，有一些还超过了 10，该现象便是 DQN 算法中的Q值过高估计。

现在我们来看一下 Double DQN 是否能对此问题进行改善。

args.dqn_type = "DoubleDQN"
agent = DQN(args)
return_list, max_q_value_list = agent.train_DQN()

episodes_list = list(range(len(return_list)))
mv_return = utils.moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Double DQN on {}'.format(args.env_name))
plt.show()

frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('Double DQN on {}'.format(args.env_name))
plt.show()

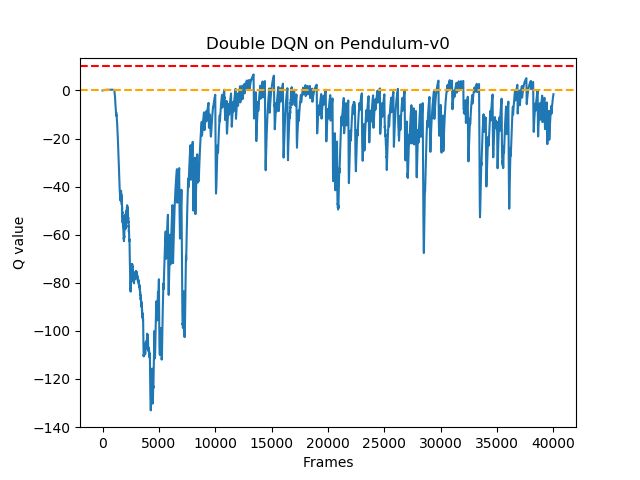
可以发现，与普通的 DQN 相比，Double DQN 比较少出现值Q大于 0 的情况，说明Q值过高估计的问题得到了很大缓解。

另外对于解决Q值过估计问题，还有一些其他的方法，比如DQL、EBQL等方法，后续咱慢慢实现。附带这两篇论文，感兴趣的可以先去看看：

• Peer O, Tessler C, Merlis N, et al. Ensemble bootstrapping for Q-Learning[C]//International Conference on Machine Learning. PMLR, 2021: 8454-8463.
• Hasselt H. Double Q-learning[J]. Advances in neural information processing systems, 2010, 23.

\quad
\quad

参考

• 《动手学强化学习》
  \quad
  \quad

持续更新~有错误的话敬请指正!