SVM过程可视化
support vector machine
- 绘制二分类时, 追求边际的分割超平面, 使用的算法是线性核下的支持向量机分类器
#1. 导入库
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs
# 2.创建分割数据
X,y = make_blobs(n_samples=40, centers=2, random_state=6)
print("X:{}, y:{}".format(X.shape,y.shape))
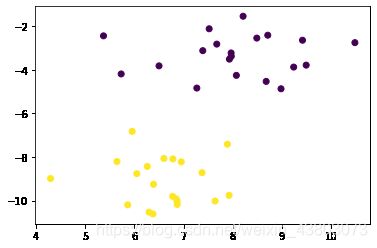
#可视化数
plt.scatter(X[:,0],X[:,1],c=y)
X:(40, 2), y:(40,)
绘制决策边界
#3. 画决策边界
#首先有散点图
plt.scatter(X[:,0],X[:,1],c=y)
ax=plt.gca()#获取当前子图,如果不存在, 则创建新的子图
#制作网格
xlim = ax.get_xlim()
ylim=ax.get_ylim()
#在最大值和最小值之间形成30个规律的数据
xx = np.linspace(xlim[0],xlim[1],30)
yy=np.linspace(ylim[0],ylim[1],30)
#使用meshgrid()将两个一维向量转为特征矩阵, 以便获取y.shape*x.shape这么多个坐标点的横纵坐标
XX,YY=np.meshgrid(xx,yy)
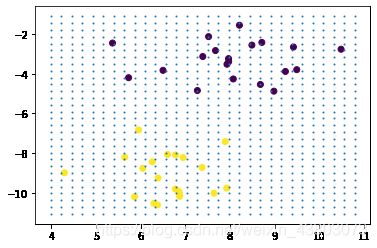
#形成网格,vstack()将多个结构一致的一维数组按行堆叠起来
xy=np.vstack([XX.ravel(),YY.ravel()]).T
plt.scatter(xy[:,0],xy[:,1],s=1,cmap='rainbow')
# 拟合模型
clf = svm.SVC(kernel='linear',C=1000)
clf.fit(X,y)
SVC(C=1000, kernel='linear')
绘制支持向量和分离超平面
plt.scatter(X[:,0],X[:,1],c=y)
#decision_function, 返回每个输入样本对应的决策边界的距离
ax=plt.gca()#获取当前子图
Z=clf.decision_function(xy)
print('Z:{}'.format(Z.shape))
#contour要求Z的结构需要与X和Y保护一致
Z=Z.reshape(XX.shape)
print('new Z:{}'.format(Z.shape))
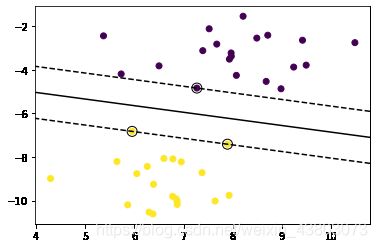
# 绘制决策边界和边际
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=1,
linestyles=['--', '-', '--'])#levels:三条等高线.
# 绘制支持向量(三个点)
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
linewidth=1, facecolors='none', edgecolors='k')
Z:(900,)
new Z:(30, 30)
clf.support_vectors_#返回支持向量
ay([[ 7.27059007, -4.84225716],
[ 5.95313618, -6.82945967],
[ 7.89359985, -7.41655113]])
# 探索建好的模型
clf.predict(X)#根据决策边界, 对X中的样本进行分类,返回的结构为n_samples
array([1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1,
1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1])
clf.score(X,y)#返回给定测试数据和target的平均准确度
1.0
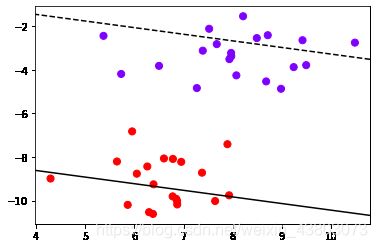
探索Z的本质(decision_function())
# Z是输入的样本到决策边界的距离, 而contour函数中的level其实是输入这个距离
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='rainbow')
ax=plt.gca()
ax.contour(XX,YY,Z,
colors='k',
levels=[-3,3],
linestyles=['--','-'])
参考
- SVM决策过程的可视化
- ax.counter()用法